|
|
2.
ТОЧКА, ПРЯМАЯ, ПЛОСКОСТЬ |
|
2.2
Прямая
Основные
положения:
-
прямую линию определяют две точки; для изображения прямой на комплексном
чертеже необходимо задать проекции её двух точек;
-
если точка принадлежит прямой, то одноименные проекции точки принадлежат
одноименным проекциям прямой;
-
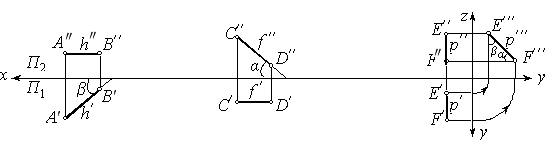
если прямая параллельна плоскости проекций, то одна из её проекций параллельна
оси, а другая проекция на соответствующей плоскости дает истинную величину
прямой (рис. 4,
5, 6);
Рис.
4 .
Горизонтальная прямая
|
Рис.
5.
Фронтальная прямая
|
Рис.
6.
Профильная прямая
|
АВ||П1
– горизонталь; |
CD||П2
– фронталь; |
EF||П3
– профильная прямая; |
А'B'–
натуральная величина прямой АВ; |
C''D''
-
натуральная величина прямой
CD; |
E'''F'''
–
натуральная величина прямой EF. |
| b
- угол наклона прямой к плоскости
П2
|
a
- угол наклона прямой к плоскости
П1
. |
|
- если
прямая перпендикулярна плоскости проекций, то проекция её на эту плоскость
- точка, а другая проекция перпендикулярна оси проекций (рис. 7
);
|
Рис.
7.
Проецирующие прямые
|
-
одноименные проекции параллельных прямых параллельны (рис. 8);
|
Рис.
8.
Параллельные прямые
|
- точки
пересечения одноименных проекций пересекающихся прямых расположены на
одной линии связи. АВ
и CD
- пересекающиеся прямые (рис. 9);
|
Рис.
9.
Пересекающиеся прямые
|
- прямой
угол проецируется на плоскость в виде прямого угла, если одна его сторона
параллельна этой плоскости, а вторая ей не перпендикулярна (рис. 10);
|
Рис.
10 . Перпендикулярные прямые
|
-
видимость
на эпюре определяется с помощью конкурирующих точек. На рис. 11
показаны a
и b -
скрещивающиеся прямые, 1
и 2
- конкурирующие точки, (•)1
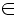 b, (•)2 b, (•)2 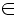 a; a;
|
Рис.
11.
Скрещивающиеся прямые
|
проекция
1′
видна первой по направлению взгляда, значит на плоскости П2
(•)1″
закрывает собой (•)2″,
а прямая b
видна первой по отношению к плоскости П2.
3
и 4
- конкурирующие точки, (•)3
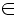 b, (•)4 b, (•)4
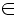 a . Проекция 3″
видна первой по направлению взгляда, значит на плоскости П1
(•)3′
закрывает собой (•)4′
, а прямая b
видна первой по отношению к плоскости П1; a . Проекция 3″
видна первой по направлению взгляда, значит на плоскости П1
(•)3′
закрывает собой (•)4′
, а прямая b
видна первой по отношению к плоскости П1;
- проекция
отрезка прямой общего положения всегда меньше отрезка в натуре. Для
определения натуральной величины прямой общего положения используют
способ прямоугольного треугольника.
На
рис. 12 изображены
прямая АВ
и плоскость проекций П1
в пространстве.
|
Рис.
12.
Определение длины отрезка
|
Построим горизонтальную проекцию A′
B′
. В плоскости проецирующих лучей точек A
и B проводим
линию АК||П1.
В прямоугольном треугольнике АВК
катет АК=
A′
B′
,
катет ВК=Zв-Zк,
а гипотенуза АB
составляет с катетом АК
угол α,
равный углу наклона прямой АB
к плоскости П1.
Построим в плоскости П1
на проекции A′
B′
прямоугольный треугольник
A′B′Bo′,
равный треугольнику АВК.
В нем гипотенуза A′Bo′
равна длине прямой АB,
а угол между проекцией A′B′
и гипотенузой A′Bo′
равен углу наклона прямой к плоскости П1.
Перейдем от пространственной схемы к комплексному чертежу прямой АB
на рис. 13.
|
Рис.
13.
Способ прямоугольного треугольника
|
На проекции A′B′
как на катете строим прямоугольный треугольник A′B′Bo′
,
в котором
B′Bo′=
ΔZ=ZB-ZA.
Гипотенуза
A′
Bo′
будет равна
натуральной величине отрезка АВ,
а угол B′A′Bo′
равен
углу наклона отрезка АВ
к горизонтальной плоскости проекций. Аналогично прямоугольный треугольник
можно построить на фронтальной проекции A″B″.
В
ΔA″Ao″B″
катет
A″Ao″=
ΔY=-YA-YB
, а гипотенуза
Ao″B″
равна натуральной величине отрезка АВ.
Угол Ao″B″
A″
равен углу наклона отрезка АВ
к фронтальной плоскости проекций.
| ЗАДАЧИ |
|
|
|
|
|
Задача 6
|
На
прямой
а найти точку, имеющую высоту 15
мм.
|
|
|
|
Задача 7
|
На
прямой а
определить точки A
и B,
у которых соответственно ZA=0
и YB=0.
|
|
|
|
Задача 8
|
Построить
недостающие проекции точек B
и C,
если известно, что точки A,
B
и C
лежат на одной прямой . |
|
|
|
Задача 9
|
Через
точку M
провести прямую l,
параллельную прямой d,
и горизонтальную прямую h,
пересекающую прямую d.
|
|
|
|
Задача 10
|
Провести
фронтальную прямую f,
отстоящую от плоскости П2
на расстояние 20
мм и пересекающую данные параллельные прямые а
и b.
|
|
|
|
Задача 11
|
На
прямой а
от точки А
отложить отрезок длиной l.
|
|
|
|
Задача 12
|
Даны
прямая АВ
и точка C.
Определить расстояние от точки C
до прямой АВ.
|
|
|
|
Задача 13
|
Построить
квадрат ABCD
со стороной на прямой m,
которая параллельна плоскости П2.
|
|
|
|
Задача 14
|
Отрезок
СМ,
параллельный П1,
является высотой равнобедренного треугольника ABC.
Точка A
принадлежит П1;
точка B
принадлежит П2.
Построить проекции треугольника ABC.
|
|
|
|
Задача 15
|
Отрезок
AC,
параллельный П2,
является диагональю ромба ABCD.
Точка B
принадлежит П1;
вершина D
равноудалена от плоскостей П1
и П2.
Построить проекции ромба.
|
|
|
|
Задача 16
|
Определить,
лежит ли точка K
на прямой MN.
|
|
|
|
Задача 17
|
Построить
горизонтальную проекцию точки С,
принадлежащей прямой АВ.
|
|
|
|
Задача 18
|
Пересечь
прямые АВ
и СD
прямой MN, отстоящей от плоскости П1
на расстояние
l.
|
|
|
|
|
Задача 19
|
Пересечь
прямые АВ
и СD
прямой MN||
П2
и отстоящей от неё на расстояние l.
|
|
|
|
Задача 20
|
Через
точку E
провести прямую, пересекающую заданные прямые АВ
и СD.
|
|
|
|
Задача 21
|
Пересечь
скрещивающиеся прямые АВ
и СD
третьей прямой, перпендикулярной к ним.
|
|
|
|
Задача 22
|
Построить
ромб АВСD, зная, что отрезок BD
является одной из его диагоналей (BD
|| П2),
а вершина А
должна быть на прямой EF.
|
|
|
Контрольные
вопросы:
1.
Чем
определяется прямая в пространстве и на чертеже?
|
2.
В
каком случае прямая проецируется на плоскости проекций в натуральную
величину, в точку?
|
3.
Линии
уровня. Дать определение. Что является графическим признаком горизонтали,
фронтали?
|
4.
Когда
точка принадлежит прямой?
|
5.
Взаимное
положение прямых. Что является графическим признаком параллельных,
пересекающихся, скрещивающихся прямых?
|
6.
В
чем суть теоремы о проекции прямого угла?
|
7.
Как
определить натуральную величину прямой методом прямоугольного
треугольника?
|
|