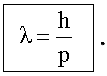ЛЕКЦИЯ N 6

Гипотеза де Бройля. Волновые свойства электронов.

Волновая функция. Соотношения неопределенностей

 

§ 1.  Гипотеза де Бройля. Волновые свойства электронов

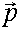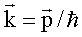Согласно гипотезе де Бройля любой движущийся частице с энергией E и импульсом  соответствует волна с частотой v = E/h, длиной волны λ = h/p   и волновым вектором . Так же как в случае с фотоном, с соответствующей волной связаны частицы, обладающие энергией  E = hv   и импульсом p = h/λ (или ).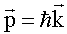

С фотонами связаны электромагнитные волны. Волны, для частиц с m ≠ 0 , о существовании которых догадался Л. де Бройль, носят название волн де Бройля. Длина волны де Бройля:

здесь p - импульс частицы.

Сопоставим свойства фотона и электрона, известные Л. де Бройлю во время публикации своих работ (1923-24 гг.)

Фотон:	Электрон:

Скорость:    v = c = 3·108м/c - inv.		Скорость:     0 ≤ v < 0
Масса:    mγ = 0		Масса:   me ≠ 0
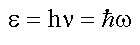
Энергия:		Энергия:
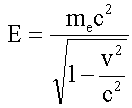
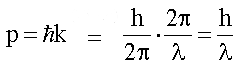
Импульс:		Импульс:

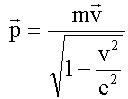
Уравнение плоской электромагнитной волны, которое является следствием уравнений Максвелла	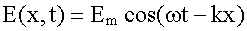	Волновые свойства электронов пока (1923 г.) не обнаружены, но, если предположить, что для электрона 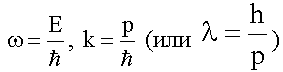, что существуют "электронные" волны 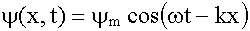, то
Интерференция и дифракция электромагнитных волн - волновые свойства фотонов.		нужно искать проявление волновых свойств электронов - интерференцию и дифракцию волн де Бройля.

 Возникает вопрос: почему мы не наблюдаем волновых свойств у макроскопических тел?

Волновые свойства - это интерференция и дифракция. Для наблюдения интерференции и дифракции волн необходимо экспериментальное устройство, создающее разность хода Δ   порядка длины волны λ.

Найдем длину волны де Бройля для тела массой m = 1г = 10^-3 кг и движущегося со скоростью v = 1 м/с.

Так как v << c, то импульс тела можно найти по классической формуле p = mv. Тогда:

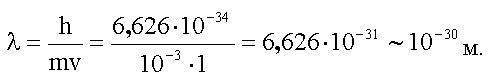
Мы видим, что длина волны де Бройля для макроскопических тел чрезвычайно мала. Для сравнения, размеры атомов и межатомных расстояний в твердых телах порядка ангстрема, 1Å = 10^-10м. Следовательно, мы не сможем создать устройство, обеспечивающее разность хода Δ ~ 10^-30 м, эта величина меньше межатомных расстояний в 10²⁰=100 000 000 000 000 000 000 раз!

Оценим длину волны де Бройля для электрона. Пусть наш электрон ускоряется разностью потенциалов U = 100 В. При такой разности потенциалов можно пользоваться ньютоновскими формулами для энергии и импульса. Выразим кинетическую энергию через импульс электрона p = mv; mv²/2 = p²/2m. Затем работу электрического поля eU  приравняем к полученной электроном кинетической энергии:

Длина волны де Бройля нашего электрона:

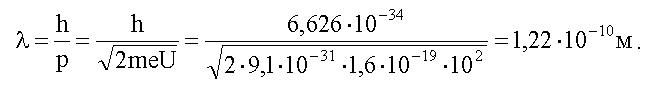
Полученная величина имеет порядок межатомных расстояний в кристалле, значит отражение "электронных волн" от поверхностных слоев атомов кристалла можно использовать для обнаружения волновых свойств электронов. Такой опыт выполнили в  1927 г. американские физики Дэвиссон и Джермер.Они  обнаружили волновые свойства электронов в эксперименте по отражению электронов от поверхности монокристалла никеля.

Волны де Бройля электронов частично отражались от поверхности монокристалла никеля, частично - от второго слоя атомов, тем самым между отраженными волнами создавалась известная разность хода  Δ = 2dsinθ (см. рисунок 6.1.). Условие максимума первого порядка интерференции двух волн имеет, как известно, следующий вид:  Δ = λ.

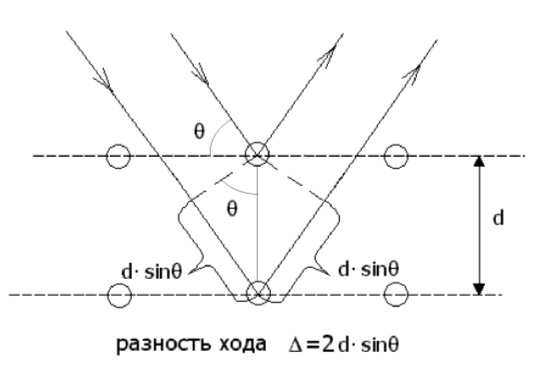
Рис. 6.1

При  Δ = 2dsinθ получим условие максимума для волн, отраженных от двух поверхностных слоев кристалла:

2dsinθ = λ.

Постоянная решетки кристалла никеля d была известна и для определенного угла θ можно было рассчитать длину волны λ, при которой должен был наблюдаться максимум. Длину волны де Бройля электронов в опыте Дэвиссона и Джермера можно очень просто изменять, изменяя ускоряющую разность потенциалов U. Опыт показал, что максимум отраженного электронного пучка наблюдался при значениях длин волн де Бройля электронов очень близких к расчетным.

Позднее волновые свойства были обнаружены у нейтронов, атомных и молекулярных пучков. Во всех случаях эксперименты подтверждали связь между длиной волны де Бройля и импульсом частицы: