ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ

ЛЕКЦИЯ N 7

Уравнение Шредингера.
Понятие об операторах физических величин.
Решение уравнения Шредингера для простейших случаев.
Частица в бесконечно глубокой одномерной потенциальной яме

 

§ 1. Уравнение Шредингера

Волновое уравнение, позволяющее найти волновую функцию частицы, которая движется в заданном силовом поле, имеет следующий вид:

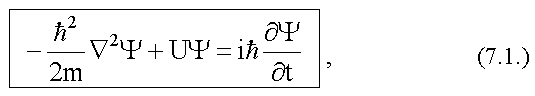
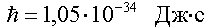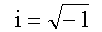здесь - постоянная Планка;  m - масса частицы; U - ее потенциальная энергия во внешнем поле, которая, вообще говоря, может зависеть и от времени t,   - мнимая единица, через обозначен оператор Лапласа. Оператор - это совокупность действий, которые надо провести над функцией. В декартовой системе координат оператор Лапласа имеет вид:

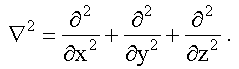
Волновое уравнение для функции Ψ получено в 1926 г. австрийским физиком Эрвином Шредингером и носит его имя - уравнение Шредингера.

В квантовой механике уравнение Шредингера играет такую же фундаментальную роль, как и уравнения движения Ньютона в классической механике.

В случае, если внешнее поле, в котором движется частица, не зависит от времени (U ≠ U(t) ), то:

Здесь E - полная энергия частицы, которая в стационарном состоянии сохраняется. Волновая функция Ψ распадается на произведение двух сомножителей. Первый сомножитель ψ(x, y, z) - координатная волновая функция. Второй сомножитель, 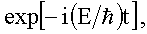дает временную зависимость волновой функции Ψ. Эта зависимость универсальна, т.е. не зависит от конкретного вида функции U(x, y, z), задающей потенциальную энергию.

Подставим в уравнение Шредингера (7.1) волновую функцию (7.2). После дифференцирования по t и сокращения на экспоненту, получим дифференциальное уравнение для координатной волновой функции ψ(x, y, z):

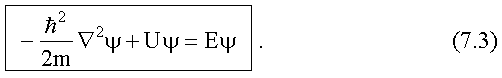
Это уравнение называют уравнением Шредингера для стационарных состояний.

Отметим, что квадраты модулей полной Ψ и координатной ψ волновых функций совпадают. Действительно:

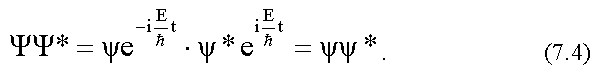
Для системы N взаимодействующих частиц волновая функция является функцией 3N координат и времени t, т.е.

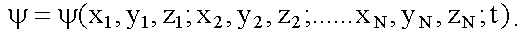
Оператор Лапласа, деленный на массу 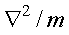, заменяется на сумму соответствующих выражений для каждой частицы, т.е.

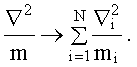
В качестве U записывается потенциальная энергия взаимодействия частиц, т.е.

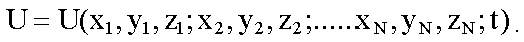
Решение получающегося уравнения представляет большие математические трудности, которые возрастают с ростом числа частиц N. В дальнейшем мы будем рассматривать только стационарное уравнение Шредингера для одной частицы, причем ограничимся простейшими потенциальными полями.

§ 2. Понятия об операторах физических величин

Уравнение Шредингера для стационарных состояний (7.3) можно записать в следующем, операторном виде:

здесь  - гамильтониан частицы, или оператор Гамильтона. Оператор Гамильтона получается из функции Гамильтона, которая есть сумма кинетической энергии частицы, выраженной через импульс, и ее потенциальной энергии, т.е.

Если в этом выражении импульс частицы p заменить на оператор импульса 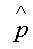, то из функции Гамильтона получим оператор Гамильтона . Оператор импульса частицы в квантовой механике выглядят следующим образом:

следовательно гамильтониандля одной частицы будет иметь следующий вид:

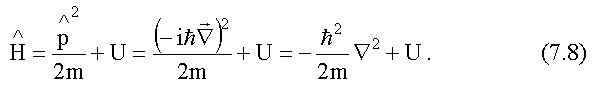
Легко убедиться, что после подстановки полученного выражения дляв уравнение Шредингера в операторном виде мы получим уравнение Шредингера в виде (7.3).