ЛЕКЦИЯ N 8

Уравнение Шредингера для атома водорода.
Квантовые числа.
Спектры атома водорода в теории Шредингера.
Волновая функция основного состояния атома водорода

 

§ 1. Уравнение Шредингера для атома водорода

В лекции N 7 мы разобрали боровскую теорию атома водорода, основанную на постулатах Бора и условии стационарности состояний атома (4.3).

Уравнение Шредингера, примененное к атому водорода, позволяет получить результаты боровской теории атома водорода без привлечения постулатов Бора и условия квантования. Квантование энергии возникает как естественное условие, появляющееся при решении уравнения Шредингера, в некотором смысле аналогичное причине квантования энергии для частицы в потенциальной яме. Применить стационарное уравнение Шредингера (7.3) к атому водорода это значит:

а) подставить в это уравнение выражение для потенциальной энергии взаимодействия электрона с ядром

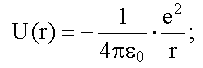
б) в качестве m подставить m_e - массу электрона (если пренебречь, как и в лекции N 4, движением ядра).

После этого получим уравнение Шредингера для атома водорода:

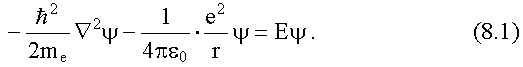
Так как потенциальная энергия зависит только от r, решение уравнения удобно искать в сферической системе координат: r, θ, φ.(рис. 8.1)

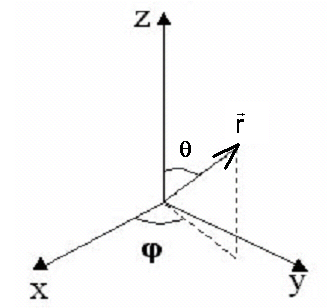
Рис. 8.1

Волновая функция в этом случае будет функцией от r, θ и φ, т.е.

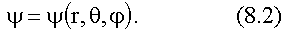
Оператор Лапласа 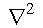необходимо записать в сферических координатах, т.е. выразить через производные по r, θ и φ. Мы не будем этого делать, поскольку получение решения уравнения Шредингера для атома водорода не входит в программу курса общей физики. Приведем лишь результаты.

Оказывается, что решение уравнения Шредингера для атома водорода существует при следующих условиях:

а) при любых положительных значениях полной энергии (E > 0). Это так называемые несвязанные состояния электрона, когда он пролетает мимо ядра и уходит от него на бесконечность;

б) при дискретных отрицательных значениях энергии

Эта формула совпадает с полученной Бором формулой для энергии стационарных состояний атома водорода. Целое число n называют главным квантовым числом.

§ 2. Квантовые числа

Волновые функции электрона ψ_nlm(r, θ, φ) определяются тремя целочисленными параметрами: n, l, m_e. Эти целые числа называются квантовыми числами:

n - главное квантовое число, оно, как мы знаем (см. (8.3)), определяет значение энергии E_n, n=1,2,3┘;

l - азимутальное (орбитальное) квантовое число, оно определяет L - модуль момента импульса электрона.

При заданном n азимутальное квантовое число l может принимать следующие значения:

всего n значений.

Следовательно, из уравнения Шредингера вытекает, что момент импульса электрона в атоме водорода квантуется и может принимать n значений. Так при n = 1 азимутальное квантовое число может принимать единственное значение l = 0. При n = 2 возможны значения l = 0,1.

m_l - это магнитное квантовое число.

Из уравнения Шредингера также следует, что проекция момента импульса L на выбранное направление в пространстве, скажем, ось z, также квантуется. Величина этой проекции, L_z, связана с квантовым числом m_l.

При заданном l магнитное квантовое число m_l может принимать следующие значения:

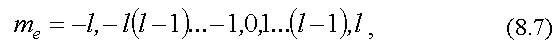
всего 2l + 1 значений.

Значит, при заданной главным квантовым числом n энергии E_n возможны n значений азимутального квантового числа (от l = 0 до n - 1) и 2l + 1 значений магнитного квантового числа m_l.. Таким образом, при заданном n число различных волновых функций ψ_nlm, отвечающих заданной энергии E_n, будет равно

Говорят, что  уровень энергии E_n будет вырожден  с кратностью n².

В атомной физике применяют заимствованные из спектроскопии условные обозначения состояний электрона с различными значениями момента импульса:

l = 0 -      s-состояние;

l = 1 -      p-состояние;

l = 2 -      d-состояние;

l = 3 -      f-состояние;

затем идут g, h и дальше в алфавитном порядке.

Значение главного квантового числа n указывают перед буквой, являющейся условным обозначением азимутального квантового числа l.

Например, 1s-состояние - это состояние с главным квантовым числом n = 1 и азимутальным квантовым числом l = 0 (на это указывает буква s).