ВОЛНОВАЯ ОПТИКА 17. ГЕОМЕТРИЧЕСКАЯ ОПТИКА

Содержание Назад Далее

17. ГЕОМЕТРИЧЕСКАЯ ОПТИКА

Это приближенное рассмотрение распространения света в предположении, что свет распространяется вдоль некоторых линий - лучей (лучевая оптика). В этом приближении пренебрегают конечностью длин волн света, полагая, что λ → 0.

Геометрическая оптика позволяет во многих случаях достаточно хорошо рассчитать оптическую систему. Но в ряде случаев реальный расчет оптических систем требует учета волновой природы света, расчет в рамках геометрической оптики дает приближенный результат, иногда неверный даже на качественном уровне.

17.1. Законы геометрической оптики

17.1.1. Закон прямолинейного распространения света

Закон прямолинейного распространения света утверждает, что в однородной среде свет распространяется прямолинейно.

Если среда неоднородна, т.е. ее показатель преломления изменяется от точки к точке, или , то свет не будет распространяться по прямой.

При наличии резких неоднородностей, таких как отверстия в непрозрачных экранах, границы этих экранов, наблюдается отклонение света от прямолинейного распространения.

17.1.2. Закон независимости световых лучей

утверждает, что лучи при пересечении не возмущают друг друга. При больших интенсивностях этот закон не соблюдается, происходит рассеяние света на свете.

17.1.3. Законы отражения и преломления

утверждают, что на границе раздела двух сред происходит отражение и преломление светового луча. Отраженный и преломленный лучи лежат в одной плоскости с падающим лучом и перпендикуляром, восстановленным к границе раздела в точке падения.

Угол падения равен углу отражения.

Отношение синуса угла падения к синусу угла преломления равно отношению показателя преломления (16.5.2) второй среды к показателю преломления первой.

Законы отражения и преломления могут нарушаться в анизотропных средах, т.е. средах, для которых показатель преломления зависит от направления в пространстве.

17.2. Полное внутреннее отражение

При увеличении угла падения i, угол преломления тоже увеличивается, при этом интенсивность (16.5.4) отраженного луча растет, а преломленного - падает (их сумма равна интенсивности падающего луча). При каком-то значении i = i_кр угол r = π/2, интенсивность преломленного луча станет равной нулю, весь свет отразится. При дальнейшем увеличении угла i > i_кр преломленного луча не будет, происходит полное отражение света.

Значение критического угла падения, при котором начинается полное отражение найдем, положим в законе преломления r = π/2, тогда Sin r = 1, значит:

.

17.3. Тонкие линзы

Линза - система двух, чаще всего сферических, преломляющих поверхностей, ограничивающих прозрачное тело. Обычно линзы делают стеклянными.

17.3.1. Собирающие и рассеивающие линзы

Линзы бывают собирающими и рассеивающими.

 

Собирающая линза в средней части толще и отклоняет лучи к оптической оси, если показатель преломления линзы больше показателя преломления среды.

 

Рассеивающая линза в средней части тоньше и отклоняет лучи от оптической оси.

 

Объясните такой ход лучей в линзах, применяя закон преломления.

Линза называется тонкой, если ее толщиной можно пренебречь. Схематически тонкая собирающая линза

изображается так:
а рассеивающая так:

17.3.2. Фокусы линзы, фокальная плоскость

Буквой F обозначены фокусы линзы - точки, в которых собираются параллельные оптической оси лучи, прошедшие через линзу (или их продолжения).

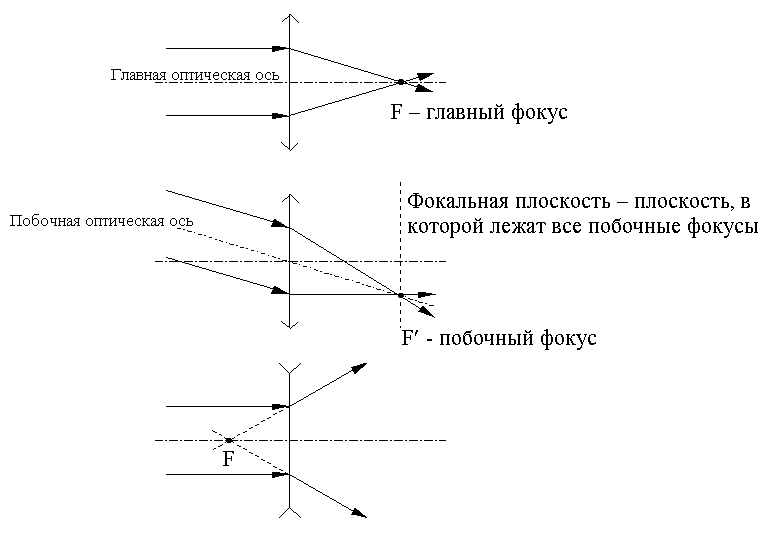
17.3.3. Фокусное расстояние тонкой линзы

Буквой F обозначают также и фокусное расстояние линзы - расстояние от фокуса до оптического центра линзы.

Для сферической тонкой линзы на основе закона преломления получается следующая формула для фокусного расстояния:

.

Здесь n_л и n_ср - показатели преломления линзы и среды, соответственно.
R₁ и R₂ - радиусы кривизны линзы, они - величины алгебраические.

Эта формула справедлива только для приосевых (параксиальных) лучей.

R₁, R₂ - радиусы кривизны сферических поверхностей линзы могут быть положительными и отрицательными. Радиус кривизны выпуклой поверхности линзы считается положительным, вогнутый - отрицательным.

Выбор знаков R₁ и R₂ в приведенной нами формуле для F иллюстрируют следующие рисунки [Следует отметить, что существует и другое, более формальное правило знаков.]):

Для собирающей линзы фокусное расстояние F положительно, для рассеивающей - отрицательно. Оптической силы линзы называют величину Ф, обратную фокусному расстоянию линзы:

,

Единица оптической силы - диоптрия (дтпр).

.

17.3.4. Построение изображения в линзах

Для построения изображения предмета необходимо построить изображение каждой его точки.

Для построения изображения точки достаточно найти точки пересечение двух любых лучей идущих из заданной точки.

Удобнее всего использовать в качестве одного из этих лучей луч, идущий через оптический центр, он идет через линзу не отклоняясь:

Другой удобный луч - идущий параллельно оптической оси. Он, преломляясь в линзе, проходит через фокус, если линза собирающая:

Если линза рассеивающая, то через фокус проходит продолжение луча:

И, если луч шел через фокус собирающей линзы, то после преломления он пойдет параллельно оптической оси:

Для рассеивающей линзы параллельно оптической оси пойдет после преломления луч, продолжение которого проходит через фокус:

17.3.4.1. Примеры построения изображения точки в собирающей линзе

17.3.4.2. Пример построения изображения точки в рассеивающей линзе

17.3.5. Формула линзы

ΔABO подобен ΔA'B'O, значит:

.

ΔOCF подобен ΔA'B'F, значит:

,     следовательно:    ,

освободимся от знаменателя:

,

поделим на d f F, тогда:

,

или

,

откуда следует формула тонкой линзы:

.

Здесь d, f, F - алгебраические величины.

Сибирская государственная геодезическая академия (СГГА), 2003.