С помощью логических переменных и символов логических операций любое высказывание можно формализовать, то есть заменить логической формулой.

Определение логической формулы:

1. Всякая логическая переменная и символы «истина» («1») и «ложь» («0») – формулы.


2. Если А и В – формулы, то A, А · В, А v В, АB, АВ – формулы.


3. Никаких других формул в алгебре логики нет.

В п. 1 определены элементарные формулы; в п. 2 даны правила образования из любых данных формул новых формул.

В качестве примера рассмотрим высказывание «Если я куплю яблоки или бананы, то приготовлю фруктовый пирог». Это высказывание формализуется в виде

(A v B)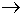C.

Такая же формула соответствует высказыванию «Если Алексей знает английский или китайский язык, то он получит место переводчика».

Как показывает анализ формулы (A v B)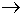C, при определённых сочетаниях значений переменных A, B и C она принимает значение «истина», а при некоторых других сочетаниях – значение «ложь» (разберите самостоятельно эти случаи). Такие формулы называются выполнимыми.

Некоторые формулы принимают значение «истина» при любых значениях истинности входящих в них переменных. Таковой будет, например, формула

А v 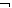A,

соответствующая высказыванию «Этот треугольник прямоугольный или косоугольный». Эта формула истинна и тогда, когда треугольник прямоугольный, и тогда, когда треугольник не прямоугольный. Такие формулы называются тождественно истинными формулами, или тавтологиями. Высказывания, которые формализуются тавтологиями, называются логически истинными высказываниями.

В качестве другого примера рассмотрим формулу

А · 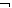A,

которой соответствует, например, высказывание «Оксана самая высокая студентка в группе, и в группе есть студентки выше Оксаны». Очевидно, что эта формула ложна, так как либо А, либо 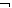A обязательно ложно. Такие формулы называются тождественно ложными формулами, или противоречиями.

Высказывания, которые формализуются противоречиями, называются логически ложными высказываниями.

Если две формулы А и В одновременно, то есть при одинаковых наборах значений входящих в них переменных, принимают одинаковые значения, то они называются равносильными.

Равносильность двух формул алгебры логики обозначается символом «=» или символом «».

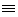Замена формулы другой, ей равносильной, называется равносильным преобразованием данной формулы.

Значения, которые принимают переменные, называют интерпретациями, например формула

f(a, b) = «a связка b»

имеет четыре интерпретации:

a = 1 (ИСТИНА);	b = 1 (ИСТИНА);
a = 1 (ИСТИНА);	b = 0 (ЛОЖЬ);
a = 0 (ЛОЖЬ);	b = 1 (ИСТИНА);
a = 0 (ЛОЖЬ);	b = 0 (ЛОЖЬ).