Формулы
можно также представлять с помощью языка логических схем. В частности,
операции конъюнкции, дизъюнкции, отрицания представляют соответствующими
логическими схемами (функциональными элементами):

Для данных логических схем существуют типовые технические схемы.
Используя данные функциональные элементы, можно создавать вычислительные
схемы, например, для формул
f1(a,
b) = (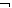 a
a 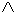 b
V a
b
V a 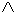
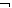 b) и
b) и
f2(a, b) = (a  b).
b).
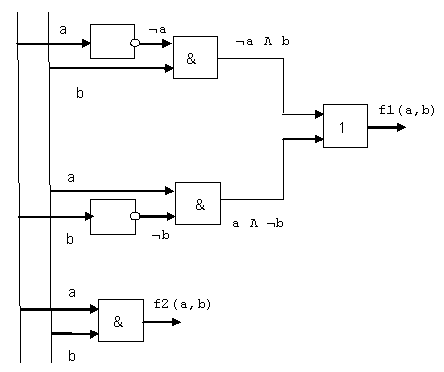
Полученную схему называют сумматором (полусумматором) так как при сложении
двух одноразрядных двоичных чисел формула f1(a, b) позволяет вычислять
сумму в младшем разряде.
То
есть:
1
+ 1 = 2 = 102 (здесь младший разряд равен
нулю),
1 + 0 = 1 (младший разряд равен единице),
0
+ 1 = 1 (младший разряд равен единице),
0 + 0 = 0 (младший разряд равен нулю).
Формула f2(a, b) позволяет производить перенос бита в старший разряд:
1
+ 1 = 2 = 102 (здесь старший разряд равен
единице).
Сравните эти данные с таблицей истинности формул
f1(a, b) = ( a
a  b
V a
b
V a 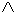
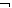 b) и
b) и
f2(a,
b) = (a 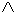 b).
b).
Для схем И – НЕ, ИЛИ
– НЕ функциональные элементы выглядят так:
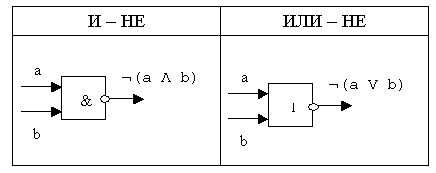
Комбинацию этих элементов используют для построения
триггеров (элементов с двумя устойчивыми состояниями 0 и 1).
На
триггерах, в частности, строятся статическая память, регистры. Так как
триггер используется для запоминания одного бита, то для формирования
1 байта необходимо использовать 8 триггеров.