ФИЗИКА в конспективном изложении. Часть 3

Содержание Назад Далее

 

ОСНОВЫ МОЛЕКУЛЯРНОЙ ФИЗИКИ
И ТЕРМОДИНАМИКИ

22. Молекулярная физика

 

22.2. Молекулярно-кинетическая теория идеального газа

22.2.1. Идеальный газ

Идеальный газ - это физическая модель (1.3) в которой:

а) пренебрегают собственными размерами молекул;

б) пренебрегают силами взаимодействия между молекулами, за исключением процесса их столкновений;

в) в процессе столкновения между собой и со стенками сосуда молекулы ведут себя как абсолютно упругие тела.

22.2.2. Давление

Давлением p, в случае равномерного распределения сил вдоль поверхности, называется величина

        

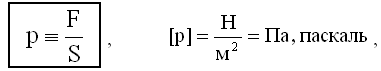
где    F - сумма приложенных перпендикулярно к поверхности сил;

S - площадь поверхности.

Прибор для измерения давления называется манометром.

22.2.3. Абсолютная температура

За единицу абсолютной (термодинамической) температуры T в системе СИ принят кельвин (К). Температура в градусах Цельсия (t, ╟C) связана с T (в К) следующим равенством:

T = t + 273,15K ,

причем 1╟С = 1К.

Прибор для измерения температуры называется термометром.

22.2.4. Уравнение состояния идеального газа - уравнение Клапейрона-Менделеева

Состояние некоторой массы идеального газа определяется тремя параметрами состояния:

p - давлением;

V - объемом;

T - абсолютной  (или термодинамической) температурой.

Связь между этими параметрами называется уравнением состояния.

Для идеального газа уравнение состояния, установленное опытным путем, имеет следующий вид:

 

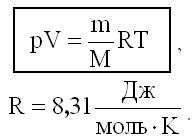
Это уравнение называется уравнением Клапейрона-Менделеева, в нем:

р - давление газа;

V - его объем;

Т - абсолютная температура;

m - масса газа;

M - молярная масса данного газа;

R -  универсальная газовая постоянная.

Уравнение Клапейрона-Менделеева является обощением опытных газовых законов: Боэля-Мариотта, Гей-Люссака, Шарля. Кроме содержания этих газовых законов в уравнении Клапейрона-Менделеева содержится информация о массе газа - m и о его сорте - M.

Проверить на опыте уравнение Клапейрона-Менделеева можно с помощью экспериментальной установки, идеализированная схема которой изображена на приведенном выше рисунке. Газ в этой установке помещен в цилиндр под подвижным поршнем. Температуру газа T измеряют термометром, объем V = Sh. Давление можно найти, поделив силу F', с которой поршень давит на газ, на его площадь S. Поршень находится в равновесии и сила F' уравновешена силой давления газа F = pS.

Опыт показывает, что при значениях T и p, близких к нормальным условиям (T₀ = 273,15К, p₀ = 101325Па ≡ 1 атмосфера), многие газы можно считать идеальными.

22.2.5. Связь давления идеального газа с концентрацией молекул и температурой - еще одна форма уравнения состояния идеального газа

Выразим из уравнения Клапейрона-Менделеева давление

Величина - дает число молей газа.

В самом деле, m - масса всего газа, а M - масса одного моля.

Домножим и поделим правую часть выражения для р на число Авогадро :

здесь N = νN_A - число молекул газа;

   - постоянная Больцмана.

Концентрация молекул

 

с учетом этого получим связь давления идеального газа с его концентрацией и температурой

 

Это еще одна форма опытного уравнения состояния идеального газа.

22.2.5.1. Закон Дальтона

Если имеется смесь нескольких газов разных сортов, то n = n₁ + n₂ + ...

Тогда

               см (22.2.5),

здесь

 - парциальное давление,

т.е. давление газа i-го сорта, которое было бы в сосуде при наличии только молекул этого сорта.

Мы получили закон Дальтона, который утверждает, что давление смеси идеальных газов равно сумме парциальных давлений.

22.2.6. Основное уравнение молекулярно-кинетической теории идеального газа

Пусть газ находится в сосуде слева от стенки, на которой мы выделим площадку S. Направим ось x вправо, перпендикулярно стенке сосуда.

Пусть молекула массой m₀ летит вдоль оси x со скоростью  по направлению к стенке (рис. а). После упругого удара о стенку скорость молекулы изменит свое направление  на противоположное  (рис. б). Причем, модули этих скоростей равны:  v₁ = v₂ = v.

По второму закону Ньютона (4.6) средняя сила <F'_x>, действующая со стороны стенки на одну молекулу равна:

здесь v - модуль средней скорости молекул.

По третьему закону Ньютона (4.7) со стороны молекулы на стенку действует в течение промежутка времени Δt средняя сила:

Давление p (22.2.2) найдем, если среднюю силу <F_x> помножим на
N_x - число ударов молекул о стенку за время Δt, а затем поделим на S:

За время Δt до стенки долетят лишь те молекулы, которые находятся от стенки не дальше, чем на расстоянии vΔt и имеют положительную проекцию скорости v_x (летят к стенке).

В силу хаотичности движения молекул можно принять, что в положительном направлении оси x, к стенке, движется 1/6 часть всех молекул, 1/6 движется против оси x, аналогично - по осям y и z. Выразим число молекул в объеме SvΔt(см. рис.) через их концентрацию n (22.2.5):

Предыдущие рассуждения велись так, как будто бы скорости всех молекул одинаковы. Чтобы учесть различие скоростей молекул надо вместо v² взять <v²> - среднее значение этой величины. Тогда для давления получим:

Полученное выражение и есть основное уравнение молекулярно-кинетической теории идеального газа:

здесь  - средняя кинетическая энергия поступательного движения одной молекулы.

Сибирская государственная геодезическая академия (СГГА), 2006.