ФИЗИКА в конспективном изложении. Часть 3

Содержание Назад Далее

 

ОСНОВЫ МОЛЕКУЛЯРНОЙ ФИЗИКИ
И ТЕРМОДИНАМИКИ

 

23.4.3. Поведение графика распределения Максвелла при изменении температуры и массы

Как видно из изложенного выше, см. (23.4.2.4), (23.4.2.5), (23.4.2.6),

В самом деле:

Из (23.4) и (23.4.2.4) получим:

Отсюда видно, что при увеличении температуры максимум функции F(v) смещается вправо (v_вер~ ) и становится ниже ( F(v_вер)~1/).

При увеличении массы молекул максимум функции F(v) смещается влево (т.к. v_вер~ ) и становится выше (т.к. F(v_вер)~1/).

Напомним, что площадь, ограниченная функцией F(v), остается постоянной и равной единице.

23.4.4. Пространство скоростей

Возьмем декартову систему координат, по осям которой будем откладывать значения компонент скоростей молекул идеального газа  v_x, v_y, v_z, находящегося в равновесном состоянии при температуре T. Скорости каждой молекулы будет соответствовать точка в этом пространстве скоростей. Состояние идеального газа, содержащего N молекул будет изображаться N точками в пространстве скоростей.

При столкновениях молекул положение точек в этом пространстве скоростей будет непрерывно меняться, но в равновесном состоянии плотность точек будет зависеть только от модуля скорости v и числа молекул N. Выделим в пространстве скоростей сферический слой радиусом v и толщиной dv (см. рисунок). Обозначим "объем" этого сферического слоя через . Как известно из геометрии:

здесь 4πv² - площадь поверхности сферы радиуса v;

dv - толщина слоя на этой сфере.

Найденное в (23.4.2.1) число молекул dN_v со скоростями в интервале от v до v+dv равно числу точек в пространстве скоростей, попадающих в "объем" d³v.

23.4.5. Плотность вероятности, отнесенная к "объему" в пространстве скоростей

Перепишем предыдущую формулу в следующем виде:

 

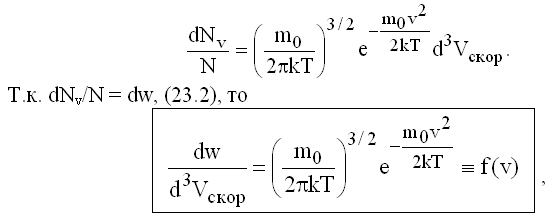
здесь f(v) - плотность вероятности, отнесенная к "объему"  в пространстве скоростей.

Если учесть, что  - кинетическая энергия одной молекулы и обозначить A = (m₀/2πkT)^3/2, то

Эта функция и позволяет найти плотность точек в пространстве скоростей. В самом деле, т.к. dw = dN_v/N, то

дает число точек в единице "объема" пространства скоростей.

23.4.6. Функция распределения по компонентам скоростей

Выделим в пространстве скоростей элемент объема в форме кубика dV'_скор=dv_xdv_ydv_z, расположенного в точке, изображающей молекулу с заданным вектором скорости .

Число молекул, имеющих скорость в пределах равно числу точек в пространстве скоростей, попадающих в выделенный нами элемент "объема" по (23.4.5) оно равно Nf(v) и число точек попадающих в элемент "объема" dv_xdv_ydv_z, будет равно:

Вероятность того, что молекула имеет вектор скорости, конец которого лежит в пределах "объема" d³V_скор=dv_xdv_ydv_z, по (23.2):

Подставим сюда f(v) из (23.4.5),  учтем, что v² = v_x² + v_y² + v_z², тогда:

Здесь мы разбили на три сомножителя выражение (m₀/2πkT)^3/2 и экспоненту. Введем обозначения:

Функции φ(v_x), φ(v_y), φ(v_z) - это плотности вероятностей распределения молекул по компонентам скоростей. Они имеют совершенно одинаковый вид, каждая из них нормирована на единицу, например:

Функции φ четные, график их симметричен относительно начала координат.

23.4.7. Распределение Больцмана

Пусть идеальный газ, имеющий определенную температуру T, находится во внешнем поле. Будем считать, что потенциальная энергия одной молекулы  - известная функция координат.

Концентрация молекул  в заданном месте пространства определяется распределением Больцмана:

 

здесь n₀ - концентрация молекул в том месте, где ε_р = 0.

Между распределением Больцмана и распределением Максвелла есть глубокое сходство.

Вероятность  того, что молекула имеет вектор скорости , конец которого лежит в "объеме" dv_xdv_ydv_z, равна:

  см. (23.4.6), (23.4.5).

Найдем  - вероятность того, что молекула имеет координаты в пределах объема dxdydz, положение которого в пространстве задает радиус-вектор .

Концентрация n по определению:

где dN - число частиц в объеме dV.

С учетом этого, формула распределения Больцмана примет следующий вид:

Поделим правую и левую части на N - полное число частиц, с учетом (23.2) получим:

Обозначим n₀/N = B, тогда получим:

Это выражение для  имеет ту же математическую структуру, что и записанное выше выражение для : некая постоянная умножается на экспоненту, в отрицательном показателе которой стоит отношение энергии отдельно взятой молекулы ε₀ к величине kT, определяющей среднюю энергию теплового движения молекул. Только в случае распределения Максвелла в экспоненте стоит кинетическая энергия одной молекулы ε_к, а у распределения Больцмана - потенциальная энергия одной молекулы - ε_p. И там, и там - элемент объема: в распределении Максвелла - это "объем" в пространстве скоростей dv_xdv_ydv_z, в распределении Больцмана - объем в реальном пространстве dxdydz. Постоянные A и B определяются условием нормировки - полная вероятность w=1.

Лабораторная работа №6-к. Распределение Больцмана.

 

23.4.8. Распределение Максвелла-Больцмана

Перемножив  и dw_z, получим  - вероятность того, что молекула имеет определенный вектор скорости  и находится в определенном месте пространства  (с точностью до dv_xdv_ydv_z и dxdydz)

это и есть распределение Максвелла-Больцмана.

23.4.9. Фактор Больцмана

Сумма кинетической энергии молекулы ε_к и ее потенциальной энергии ε_r есть полная энергия молекулы ε, т.е. ε = ε_к+ε_r.

Записав показатель экспоненты в распределении Максвелла-Больцмана через полную энергию молекулы ε получим фактор Больцмана:

имеющий важное значение в статистической физике. Величине фактора Больцмана пропорциональна вероятность обнаружить систему в состоянии с энергией ε.

Как будет показано во второй половине настоящего пособия (см. 28.5.3.3) энергия микрочастиц квантуется, т.е. имеет определенные значения. С учетом этого фактор Больцмана приобретает следующий вид:

здесь ε_i - изменяющаяся дискретно, скачками энергия макроскопической системы, находящейся в состоянии с номером i.

23.4.10. Барометрическая формула

Применим распределение Больцмана для идеального газа, находящегося в однородном поле тяжести. В этом случае потенциальная энергия одной молекулы:

               см. (5.7.1),

здесь g - ускорение силы тяжести,

h - высота над тем уровнем, где ε_р = 0.

Из (23.4.7) для концентрации молекул n будем иметь

Из (22.2.5) давление газа: p=nkT пропорционально концентрации n.

Следовательно, для зависимости давления p от высоты h имеем:

 

Это и есть барометрическая формула, в ней p₀ - давление в том месте, где h = 0.

Если домножить и поделить показатель степени в экспоненте на число Авогадро N_A, то получим барометрическую формулу в несколько ином виде:

 

здесь M = m₀N_A - масса одного моля газа,

R = kN_A - универсальная газовая постоянная.

Лабораторная работа №71-к. Распределение Максвелла.

Сибирская государственная геодезическая академия (СГГА), 2006.