|
|
| Приложение
1. Эпюр
1
Ортогональное
проецирование. Позиционные
и метрические задачи
(Индивидуальная графическая работа)
|
|
1.
Назначение и основные требования
Индивидуальная
графическая работа по начертательной геометрии (Эпюр 1) предназначена
для домашней самостоятельной работы студентов и является контролем их
знаний по теме "Ортогональное проецирование. Позиционные и метрические
задачи".
Прежде, чем выполнить задание, студент должен ознакомиться с теоретической
частью темы [1,2,3,4,5],
а в аудитории решить типовые задачи, представленные в "Сборнике
задач".
При защите индивидуального задания студент должен объяснить выполненные
построения и ответить на контрольные вопросы по теме.
Индивидуальная графическая работа (Эпюр 1) оформляется в соответствии
с требованиями стандартов ЕСКД [6,7,8,9].
Индивидуальная графическая работа (Эпюр 1) выполняется в карандаше на
листе чертёжной бумаги формата А3
(297×420) мм, в нижнем правом углу которого помещается
основная надпись по форме 1.
Индивидуальная графическая работа (Эпюр 1) состоит из трёх задач. Каждая
задача вычерчивается в системе двух главных плоскостей проекций (горизонтальной
и фронтальной) и выполняется отдельным комплексным чертежом. Чертежи
вычерчиваются в масштабе 1:1
и равномерно размещаются в пределах формата листа.
Все видимые основные линии построений должны быть выполнены сплошными
линиями толщиной S=(0,8-1)
мм, а линии связи - тонкими толщиной S/3
мм; линии невидимых контуров показывают штриховыми линиями
толщиной S/2
мм. Точки на чертеже желательно вычерчивать в виде окружностей
ø1,5-2
мм. Все основные вспомогательные построения должны быть
сохранены.
ЗАДАЧИ
к Эпюру 1
Варианты
индивидуальных заданий к Эпюру 1
| |
| |
Задача
1 |
 |
|
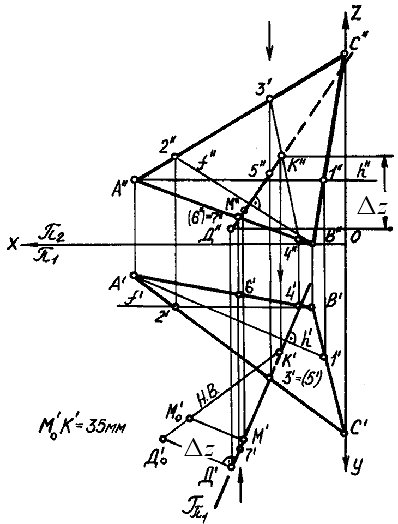
Определить
расстояние от точки D
до плоскости Δ
АВС.
|
Указания
к решению задачи: |
| 1) |
Прежде
всего через
точку D
надо провести прямую, перпендикулярную к плоскости ΔАВС,
для этого:
|
 начертим на листе оси координат x,
y, z и согласно своему варианту возьмём координаты
точек А,
Б, С, D;
по координатам построим Δ
АВС и точку D
в двух проекциях;
построим на эпюре проекции горизонтали h
и фронтали f
и через проекции точек D'
и D"
проведём проекции перпендикуляра.
Горизонтальная
проекция перпендикуляра составит прямой угол с горизонтальной
проекцией горизонтали h',
а фронтальная проекция перпендикуляра составит прямой угол с
фронтальной проекцией фронтали f"
(в соответствии с теоремой о проецировании прямого угла).
|
| 2) |
Затем
надо найти точку пересечения (точку встречи) перпендикуляра
с плоскостью ΔАВС
и определить видимость перпендикуляра относительно плоскости
ΔАВС
в проекциях, для этого:
|
проведём через перпендикуляр вспомогательную проецирующую
плоскость (горизонтально проецирующую или фронтально проецирующую);
построим линию пересечения
(3-4) данной плоскости ΔАВС
и вспомогательной плоскости, (точка
встречи К
определится при пересечении перпендикуляра и построенной прямой
(3-4));
на эпюре через горизонтальную проекцию
перпендикуляра проведём горизонтально проецирующую плоскость
ГП1
и построим линию пересечения
(3-4) плоскости ΔАВС
проецирующей плоскостью ГП1.
Фронтальная
проекция точки встречи К"
лежит на пересечении фронтальной проекции перпендикуляра и
фронтальной проекции линии (3"-4").
Горизонтальная проекция К'
определяется по линии связи.
Видимость
перпендикуляра и плоскости ΔАВС
определяется по конкурирующим точкам. Видимость горизонтальной
проекции А'С'
стороны ΔАВС
и горизонтальной проекции отрезка D'К'
перпендикуляра относительно горизонтальной плоскости проекций
определяется конкуренцией точек 3"
и 5".
Видимость фронтальной проекции А"В"
стороны Δ
АВС и фронтальной проекции отрезка D"K"
определяется конкуренцией точек
6' и 7'.
|
| 3) |
Наконец,
надо определить натуральную величину отрезка от точки D
до точки встречи методом прямоугольного треугольника,
для этого:
|
на горизонтальной проекции перпендикуляра
D'К'
строим прямоугольный треугольник Д'К'Do',
в котором катет D'Do'
равен расстоянию Δ
z=zk-zd,
а гипотенуза Do'К'
будет равна натуральной величине отрезка
DК.
|
| |
| |
| |
Задача
2 |
|
|
Построить
плоскость, параллельную плоскости ΔАВС
и отстоящую от нее на 35
мм.
|
Указания
к решению задачи: |
| 1) |
Прежде
следует построить точку, находящуюся на расстоянии 35
мм от плоскости ΔАВС,
для этого воспользуемся эпюром задачи 1:
|
отложим на гипотенузе Do'К'
отрезок Mo'K',
равный 35
мм и , проведя Mo'M' ||
Do'К', получим горизонтальную проекцию M'
точки, лежащей на расстоянии 35
мм от плоскости ΔАВС;
по линии связи найдём фронтальную проекцию
точки М";
координаты точек
M' и М"
перенесём на эпюр задачи 2.
|
| 2) |
Затем
следует задать плоскость двумя пересекающимися прямыми, проходящими
через точку, находящуюся на расстоянии 35
мм от плоскости ΔАВС:
|
чтобы плоскость была параллельна плоскости ΔАВС,
эти две пересекающиеся прямые должны быть параллельны любым
двум пересекающимся прямым, принадлежащим плоскости ΔАВС;
построение
плоскости, параллельной плоскости ΔАВС
, понятно из рисунка.
|
| |
| |
| |
Задача
3 |
 |
|
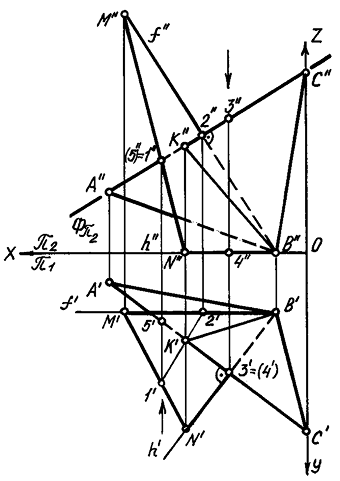
Через
вершину В
ΔАВС
провести плоскость, перпендикулярную стороне AC.
Эту плоскость задать треугольником. Построить линию пересечения
двух треугольников и показать их видимость в проекциях.
|
Указания
к решению задачи: |
| 1) |
Плоскость
перпендикулярна прямой, если две пересекающиеся прямые на плоскости
перпендикулярны этой прямой. Поэтому прежде всего, через точку
В
надо провести две прямые, перпендикулярные стороне AC:
|
в соответствии с теоремой о проецировании прямого угла в качестве
двух прямых, перпендикулярных стороне AC,
надо использовать прямые частного положения - горизонтальную
и фронтальную;
на эпюре горизонтальная проекция горизонтальной
прямой h'
составит прямой угол с горизонтальной проекцией стороны А'C',
а фронтальная проекция фронтальной прямой f"
составит прямой угол с фронтальной проекцией стороны А"C".
|
| 2) |
Далее
следует образовать плоскость в виде треугольника, имеющего общую
точку В
с заданным ΔАВС,
а две другие точки надо взять произвольно на построенных двух
прямых:
|
на построенных прямых h
и f
надо взять произвольно две точки M
и N,
построить их проекции;
образованный Δ
MNB будет перпендикулярен Δ
АВС.
|
| 3) |
Затем
надо построить линию пересечения двух треугольников. Для этого
надо найти две точки, принадлежащие линии пересечения, т.к.
точка В
принадлежит обоим треугольникам, следовательно, она принадлежит
линии пересечения двух треугольников. Чтобы найти вторую точку,
принадлежащую линии пересечения, надо решить задачу на нахождение
точки встречи, например, стороны AC
ΔАВС
с плоскостью второго треугольника:
|
на эпюре для нахождения точки встречи
через фронтальную проекцию А"C"
надо провести вспомогательную фронтально проецирующую плоскость
ФП2;
затем нужно построить линию пересечения (1-2)
плоскости Δ
MNB с этой фронтально проецирующей плоскостью;
горизонтальная проекция точки встречи
К'
стороны АC
с плоскостью Δ
MNB будет находиться на пересечении горизонтальной
проекции А'C'
c горизонтальной проекцией линии (1'-2');
фронтальная
проекция К"
определится по линии связи;
соединив точки B
и К,
получим отрезок BК,
который будет являться искомой линией пересечения.
|
| 4) |
Показать
видимость сторон треугольников в проекциях :
|
видимость сторон треугольников определяется способом конкурирующих
точек;
видимость проекций А'C' и B'N'
относительно горизонтальной плоскости проекций П1
определяется конкуренцией точек 3"
и 4",
а видимость проекций А"C"
и M"N"
относительно фронтальной плоскости проекций П2
определяется конкуренцией точек 1'
и 5'.
|
| |
|
