Энтропия

Первое начало термодинамики ничего не говорит о направлении протекания процесса. О направлении протекания процессов говорит второе начало термодинамики.

Второе начало термодинамики:

Теплота не может переходить от менее нагретого тела к более нагретому телу.

Рассмотрим два резервуара в изолированной системе.

 

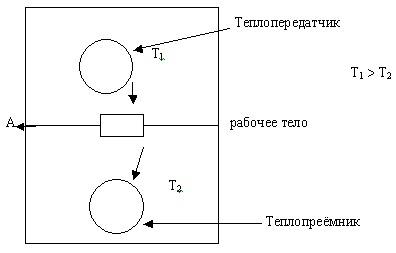
По мере перекачки энергии горячий резервуар охлаждается, а холодный нагревается. Следовательно, разность температур резервуаров уменьшается в течение всего периода времени, когда совершается работа.

Это означает, что количество энергии, которое может быть потрачено на работу (оно зависит от разности температур), должно всё время уменьшаться.

Энергия, которая уже перешла от теплопередатчика к приёмнику и превратилась в работу, называется связанной, или недоступной энергией, так как превратиться в работу она не может.

Для обозначения этой связанной, или недоступной, энергии Клаузиус ввёл следующую термодинамическую функцию, которую назвал энтропией S (превращение).

Энтропия – отношение теплоты к температуре, при которой происходит переход энергии

 

S = Q/T Дж/моль к.

Физический смысл энтропии настолько сложен, что долгое время не был объяснён. Объяснил его Больцман. Он назвал энтропию термодинамической вероятностью существования системы, то - есть данному макросостоянию системы отвечает множество микросостояний.

Под микросостоянием системы понимается скорость и траектория каждой микрочастицы, составляющей систему, а также взаимное положение микрочастиц, число их столкновений и т.д.

Энтропия по Больцману : S = K · lnW,

где

W – вероятность состояния данной системы,

K – постоянная Больцмана.

Энтропия – мера неупорядоченности системы.

Определяется и рассчитывается абсолютная энтропия, приведённая к нормальным условиям.

Положительной энтропией обладают все реальные системы.

C (алмаз) – S⁰_(c) = +2,38 Дж/моль к.

Отсюда вытекает третье начало термодинамики:

Нулевой энтропией обладают идеальные кристаллы при абсолютном нуле.

В реальных условиях в изолированной системе величина связанной, или недоступной, энергии возрастает, то – есть самопроизвольно энтропия может только возрастать

 

.

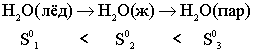Данный процесс происходит с увеличением энтропии: ΔS⁰ > 0, обратный процесс ΔS⁰< 0.

Для самопроизвольных процессов в изолированной системе

ΔS⁰₂₉₈ > 0 – необратимый процесс,

ΔS⁰₂₉₈ = 0 - обратимый процесс.

Поскольку энтропия - функция системы, т.е. зависит от начального и конечного состояний системы, то изменение энтропии химического процесса зависит от вида и состояния исходных веществ и продуктов реакции.

aA + bB = cC +dD;

ΔS⁰_х.р. = (cS⁰_C + dS⁰_D) – (aS⁰_A + bS⁰_B) Дж/к.

Для изолированных систем изменение энтропии позволяет предсказать, будет ли процесс необратимым или обратимым.

Если изменение энтальпии равно нулю, то процесс обратимый.

Эти критерии не могут быть использованы для закрытых систем.

Для закрытых систем вводится новая термодинамическая функция – энергия Гиббса (изобарно – изотермический потенциал).

Рассмотрим закрытую систему, в которой процесс протекает при постоянной температуре.

Согласно второму началу термодинамики разрешены следующие превращения:

• для обратимого процесса: ΔS= Q/T; Q_p =ΔS⁰T; Q_p - ΔS⁰T= 0 ; ΔH⁰ - ΔS⁰T= 0;
  
• для необратимого процесса: ΔS> Q/T; ΔS⁰T> Q; Qp < ΔS⁰T; Qp- ΔS⁰T<0; ΔH⁰-ΔS⁰T<0.

Разница между энтальпией и энтропией, помноженной на температуру, и есть энергия Гиббса

ΔH⁰ -ΔS⁰T = ΔG⁰.

Измеряется и рассчитывается только изменение энергии Гиббса:

ΔG⁰₂₉₈ кДж/моль.

Для простых веществ изменения энергии Гиббса равны нулю. Изменение энергии Гиббса, также как и энтропии, говорит о направлении протекания процесса.

Самопроизвольный необратимый процесс возможен только в том случае, если изменение энергии Гиббса меньше нуля

ΔG < 0.

 

Знак изменения функции			Возможность протекания реакции	Пример реакции
ΔH0	ΔS0	ΔG
+	-	+	Невозможно ни при каких условиях	N2+2O2=2NO2
-	+	-	Возможно при любых условиях	C2H2+7.5O2=6CO2+3H2O
-	-	+ -	Возможно при низких температурах	3H2+N2=2NH3
+	+	+ -	Возможно при высоких температурах	N2O4=2NO2

 

Поскольку ΔG – функция системы, то эта функция также зависит от начального и конечного состояний химической реакции, то - есть от исходных веществ и продуктов реакции.