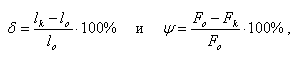Испытание на растяжение – метод, получивший широкое распространение для конструкционных сталей, цветных металлов и их сплавов. При этом используют образцы круглой и плоской формы. По результатам одного опыта испытание на растяжение позволяет установить ряд важных характеристик металла. На рис. 20 представлена диаграмма деформации, фиксирующая зависимость между приложенным напряжением ? и деформацией образца ? вплоть до его разрушения. Сплошной линией обозначена кривая условных напряжений, пунктирной – истинных.

Рис. 20. Типичная кривая растяжения с площадкой текучести для конструкционной стали (не в масштабе)

Сплошная кривая характеризует поведение металла под действием напряжений, определённых как отношение нагрузки к исходной площади образца без учёта его сужения и потому получивших название условных. При испытании на растяжение обычно пользуются диаграммой условных напряжений.

Из рисунка видно, что на начальном участке (до точки А) деформация прямо пропорциональна напряжению. Тангенс угла наклона прямой ОА к оси абсцисс или, другими словами, коэффициент пропорциональности между напряжением ? и относительной деформацией ? вдоль оси нагружения при одноосном нагружении, ?/? получил название модуля упругости материала Е. В специальной литературе можно встретить другое название этой характеристики: модуль растяжения, модуль Юнга – в честь английского учёного Томаса Юнга (1773–1829), изучавшего упругое поведение стержней.

Модуль упругости в большинстве случаев не зависит от структуры металла, т. е. не является структурно чувствительной характеристикой, а определяется силами межатомной связи. Значения модулей упругости для широко распространённых веществ приведены в табл. 1.

Модуль упругости является очень существенной величиной для оценки материалов, используемых в конструкциях. Так, при одних и тех же значениях напряжений, тот материал даст меньшую упругую деформацию, например, провисание балки, у которого больше модуль упругости.

Линейное соотношение между напряжением и деформацией ? = E•? называют законом Гука – в память о работах другого английского ученого Роберта Гука (1635–1703), впервые установившего линейную зависимость между нагрузкой и удлинением. Предельное напряжение в области упругой деформации (точка A на рис. 20), где выполняется линейная зависимость между приложенным напряжением и вызываемой им деформацией, т. е. закон Гука, называется пределом пропорциональности. Его обозначают ?_пц.

Модуль упругости

Материал	Е, ГПа	Материал	Е, ГПа
Железо, сталь 20	210	Цинк	82
Медь листовая	113	Магний	45
Латунь	97	Вольфрам	390
Титан	100	Свинец	17
Алюминий	68	Особо чистое кварцевое стекло	74.5
* ГПа = 100 кгс/мм2

Предельное напряжение, соответствующее нагрузке, при снятии которой тело еще восстанавливает свои первоначальные размеры, называется пределом упругости. Предел упругости может совпадать с пределом пропорциональности или быть несколько выше его (точка B на рис. 20). Во втором случае при напряжениях, близких к пределу упругости, наблюдается отклонение от закона Гука. Предел упругости принято определять как напряжение, вызывающее остаточную деформацию, равную 0,05 % от первоначальной длины образца (?_{0, 05}).

После краткой характеристики модуля упругости, предела пропорциональности и предела упругости необходимо сделать следующее принципиальное замечание. С появлением точных методов измерения было установлено, что чисто упругой деформации, бесследно исчезающей после снятия нагрузки, не существует. Более того, точные измерения показывают, что вся кривая растяжения имеет не плавный, а ступенчатый характер, а каждая ступенька соответствует серии сдвигов, происходящих практически одновременно. Поэтому данные выше определения упругих характеристик являются в известной степени условными.

Дальнейшее увеличение нагрузки приводит к тому, что деформация растет быстрее, чем напряжение. В точке C возникает значительное удлинение без заметного увеличения растягивающей нагрузки. На участке CD материал становится пластичным. Он течёт: на диаграмме «напряжение – удлинение» наблюдается так называемая площадка текучести. Наименьшее напряжение, при котором происходит необратимая пластическая деформация образца без заметного увеличения растягивающей нагрузки, называют пределом текучести. Ярко выраженную площадку текучести имеют, как правило, пластичные металлы и сплавы. Деформация обусловлена интенсивным размножением и перемещением дислокаций. Площадка текучести может быть устранена предварительной слабой деформацией, закалкой
и другими приёмами.

Для материалов, на диаграмме растяжения которых площадка текучести отсутствует, определяют условный предел текучести ?_0.2, который соответствует напряжению, вызывающему остаточное удлинение 0,2 %.

Для того чтобы при снятии нагрузки конструкция (деталь) возвращалась к исходным размерам, относительные деформации должны находиться в области линейного закона упругости. Поэтому в основе инженерных расчётов принимают напряжения, не превышающие предела текучести. На практике нельзя допускать напряжений, приближающихся
к пределу текучести.

В точке D материал начинает упрочняться, проявляя дополнительное сопротивление увеличению нагрузки. В точке E напряжение достигает максимального значения, или предела прочности ?_B, который называют также временным сопротивлением. Дальнейшее вытягивание образца сопровождается уменьшением нагрузки, и в точке F начинается его разрушение.

Под пластичностью понимают способность материала, не разрушаясь под действием внешних сил, изменять форму и размеры. В качестве меры пластичности принимают относительное удлинение (укорочение) и поперечное сужение (уширение) при статическом испытании на растяжение (сжатие), а также ударную вязкость при динамическом испытании. Чаще всего пластичность характеризуют относительным удлинением ? и относительным сужением поперечного сечения ?, выражающимися в процентах по приведенным ниже уравнениям:

где    l_o и l_k – длина образца до и после разрыва;

F_o и F_k – площадь поперечного сечения образца до и после разрушения.

У хрупких материалов относительное удлинение и сужение близки к нулю, у пластичных достигают десятков процентов.

Максимальной пластичностью обладают материалы с ГЦК-решёткой, промежуточной – с ГПУ, наименьшей – с ОЦК. Наибольшая величина пластической деформации, предшествующей разрушению, называется пределом пластичности. Предел пластичности является функцией температуры и условий деформации (например, растяжением, сжатием).

Пластическая деформация учитывается при выборе материала для изготовления изделий в операциях вытяжки, штамповки, гибки и т. д.

Предел прочности ?_B или временное сопротивление разрыву – понятие чисто условное, соответствующее отношению максимальной нагрузки, предшествующей разрушению, к исходному, а не к действительному в момент разрыва сечению образца.

Поскольку обычная кривая растяжения (рис. 20) не учитывает постепенного уменьшения сечения образца, то может создаться неверное впечатление о том, что с увеличением степени деформации напряжения в испытуемом образце уменьшаются. Если же вычисления производить делением действующей в данный момент силы на площадь поперечного сечения в тот же момент, мы получим кривую истинных напряжений, показанную на рис. 20 штриховой линией. Эта кривая, совпадая на начальном участке с обычной кривой, свидетельствует о том, что в действительности в материале напряжения возрастают вплоть до точки разрушения.

Отсюда следует, что для пластичных материалов получаемые в процессе обычных опытов на разрыв значения напряжений и прочности не дают верных представлений об этих характеристиках, поскольку сечение образца в момент разрыва сильно отличается от исходного. Для хрупких же материалов, например, сильно наклёпанных металлов, у которых в момент разрыва сечение мало изменяется, такой метод может дать представление об истинной практической прочности.

Необходимо также сделать замечание, касающееся термина «временное сопротивление». Прочность является функцией времени нахождения под нагрузкой, что не отражается на диаграммах деформации. При кратковременном воздействии один и тот же образец может выдержать гораздо большие нагрузки, чем при длительном. При низких температурах (< 0,3Т_пл) влияние времени менее ощутимо, чем при высоких. Поэтому для низких температур предел прочности можно считать с достаточной точностью характеристикой материала без указания времени испытания. При высоких температурах обязательно указывается время испытания, и термин «временное сопротивление» является более подходящим по смыслу, чем термин «предел прочности».

Определение истинных напряжений имеет особое значение для прочностных расчётов, технологии обработки металлов и анализа протекающих в металле процессов.

Таким образом, при испытании на растяжение деформация образца сначала является макроупругой. При дальнейшем нагружении деформация постепенно переходит в пластическую, происходящую по дислокационному механизму. Накопление дислокаций приводит к упрочнению металла, а при значительной их плотности – к развитию трещин и его разрушению.

Изменяя формы образца и виды нагружения подобным образом определяют характеристики материала при изгибе, сжатии, кручении и других видах механических испытаний.