ЛЕКЦИЯ N 12

§ 3.  Бозоны. Распределение Бозе-Эйнштейна

Бозон - это частица или (квазичастица - как, например, фонон - квант упругих колебаний в твердых телах) с нулевым или целочисленным спином. К бозонам, как уже упоминалось, относятся также фотоны (спин s = 1), составные  частицы,  состоящие  из  четного  числа  фермионов  (например,  атом ⁴₂He), куперовские пары электронов, образование которых приводит к сверхпроводимости.

Распределение Бозе-Эйнштейна дает <n(E_i)> среднее число невзаимодействующих между собой бозонов в состоянии с энергией E_i , где i - набор квантовых чисел, характеризующих квантовое состояние. Формула распределения Бозе-Эйштейна имеет следующий вид:

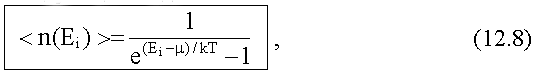
где µ - химический потенциал; T - абсолютная температура; k - постоянная Больцмана.

В отличие от распределения Ферми-Дирака в знаменателе стоит "минус единица". Вследствие этого химический потенциал µ для бозонов не может быть положительным. Иначе при E_i < µ (если бы µ > 0!) показатель экспоненты в знаменателе стал бы отрицательным, экспонента стала бы меньше единицы и некоторые из чисел заполнения n_i стали бы отрицательными, что невозможно.

Если полное число частиц в системе не фиксировано, как, например, для фотонов при тепловом излучении, то химический потенциал µ равен нулю.

При фиксированном числе частиц величину µ определяют из условия нормировки, как и в случае распределения Ферми-Дирака.

Применим распределение Бозе-Эйнштейна для вывода формулы Планка для u(ω, Т) - функции распределения плотности энергии в спектре излучения абсолютно черного тела.

При обычных, не лазерных, интенсивностях фотоны можно считать невзаимодействующими между собой бозонами, поэтому тепловое излучение, находящееся в равновесии со стенками излучающей полости можно рассматривать как идеальный фотонный газ.

Как было отмечено выше, химический потенциал для системы фотонов µ = 0. Энергия фотона 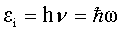, следовательно,  распределение Бозе-Эйнштейна для фотонов имеет следующий вид:

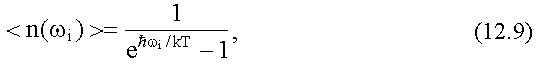
здесь <n(ω_i)> - среднее число фотонов с частотой ω_i. Частота ω_i  задает квантовое состояние фотона.

Пусть ΔE обозначает энергию фотонов, находящихся в объеме ΔV и имеющих частоты, лежащие в интервале Δω.

Тогда

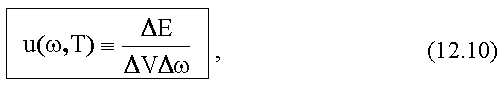
имеет смысл функции распределения плотности энергии в спектре излучения абсолютно черного тела (спектральное распределение).

Пусть ΔZ(ω_i) - число квантовых состояний фотонов в объеме ΔV и интервале частот от ω_i до ω_i + Δω.

Тогда

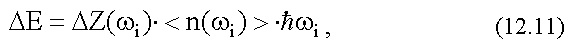
так как произведение 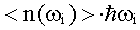  дает среднюю энергию фотонов частоты ω_i, т.е. среднюю энергию в одном квантовом состоянии. Функция <n(ω_i)> известна, поэтому задача состоит в нахождении числа квантовых состояний ΔZ(ω_i).

Подсчет числа квантовых состояний ΔZ делается с использованием формулы (10.5), т.е.:

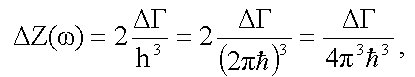
здесь двойка учитывает две возможные поляризации фотонов. Фазовый объем.

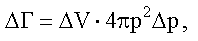
где - объем сферического слоя в пространстве импульсов.

Импульс фотона (см. (5.3)):

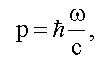
значит

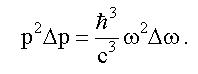
Тогда

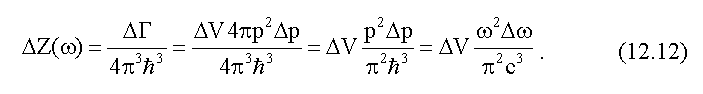
Так как частоты ω_i меняются квазинепрерывно, то мы опустили индекс i, нумерующий квантовые состояния.

Подставляя в формулу (12.11) для ΔE полученное выражение ΔZ(ω) (12.12) и функцию распределения Бозе-Эйнштейна для фотонов (12.9), получим:

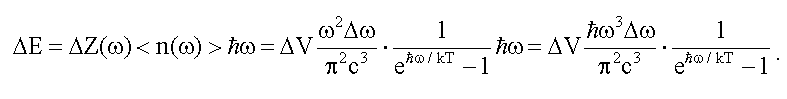
Используя это выражение, получим формулу Планка для функции распределения плотности энергии в спектре излучения абсолютно черного тела:

 

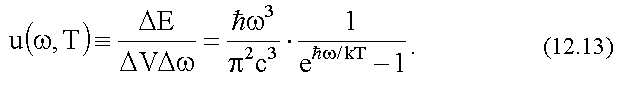
Из нее, как показано в лекции N 2, § 1, следует формула для спектральной плотности энергетической светимости абсолютно черного тела (см. (2.1), (2.2)).

Итоги лекции N 12

1. Квантовая теория электропроводности металлов дает для удельной проводимости σ формулу (12.2):

   

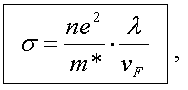
   здесь m* - эффективная масса электрона, которая учитывает влияние сил, действующих на электрон со стороны ионных остовов кристаллической решетки; λ - длина свободного пробега электрона в металле; v_F - средняя скорость электронов вблизи уровня Ферми.

   В этой формуле от температуры зависит только λ, причем, эта зависимость при T ≥ 100K линейна. Следовательно, квантовая теория объясняет наблюдаемую на опыте линейную зависимость удельного сопротивления металлов от температуры.

2. Термоэлектронной эмиссией называется испускание электронов нагретыми телами.

3. Квантовая теория дает следующую формулу для плотности тока насыщения при термоэлектронной эмиссии (формула Ричардсона-Дэшмена, см. (12.7)):

   

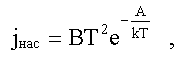
   здесь А - работа выхода электрона из металла, В - константа Ричардсона, для которой в квантовой теории получается формула (12.6):

   

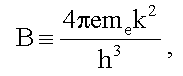
   численное значение константы Ричардсона:

   

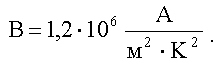
4. Для частиц с нулевым или целым спином - бозонов - справедливо распределение Бозе-Эйнштейна (см. (12.8)):

   

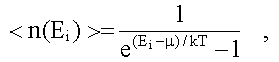
   здесь  <n(E_i)>- среднее число невзаимодействующих между собой бозонов в квантовом состоянии с энергией Е_i; µ - химический потенциал.

5. Распределение Бозе-Эйнштейна позволяет получить u(ω,T) - функцию распределения плотности энергии в спектре излучения абсолютно черного тела (см. (12.13)):