ВОЛНОВАЯ ОПТИКА 21. ВЗАИМОДЕЙСТВИЕ СВЕТА С ВЕЩЕСТВОМ

Содержание Назад Далее

21. ВЗАИМОДЕЙСТВИЕ СВЕТА С ВЕЩЕСТВОМ

При распространении света в веществе возникают следующие явления. Во-первых, изменяется скорость распространения, см. (16.5.2), причем, скорость распространения зависит от длины световой волны. Это явление называется дисперсией.

Во-вторых, часть энергии световой волны теряется. Это явление называется поглощением или абсорбцией света.

Наконец, при распространении света в оптически неоднородной среде возникает рассеяние света на пространственных неоднородностях среды.

 

21.1. Дисперсия света

Дисперсией света называют зависимость показателя преломления n от длины волны (или от частоты), т.е.

n = n(λ).

У прозрачных веществ примерный вид зависимости изображен на следующем рисунке:

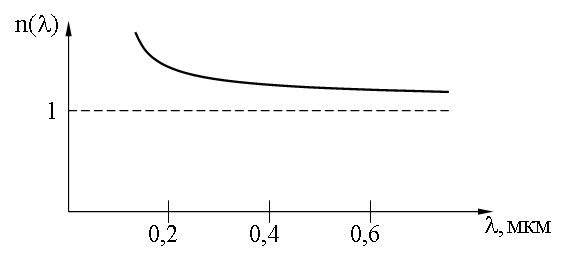
Такая зависимость n(λ), когда n уменьшается с ростом λ называется нормальной дисперсией. При прохождении белого света через призму свет разлагается в дисперсионный (призматический) спектр. Это явление впервые наблюдал И. Ньютон (1672 г.). Схема его опыта изображена на рисунке:

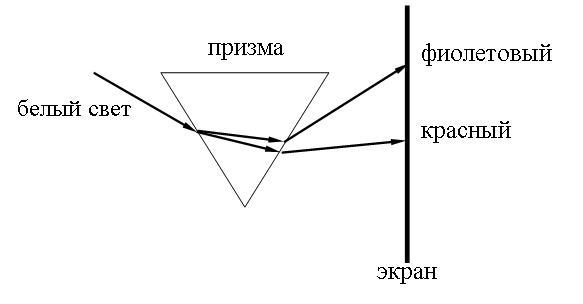
21.1.1. Классическая электронная теория дисперсии

Последовательное описание взаимодействия света с веществом возможно только в рамках квантовой теории. Однако, во многих случаях можно ограничиться описанием в рамках волновой (электромагнитной) теории излучения и классической электронной теории , согласно которой каждую молекулу среды можно рассматривать как систему зарядов, имеющих возможность совершать гармонические колебания - как систему осцилляторов с различными собственными частотами и коэффициентами затухания. Движение этих осцилляторов можно рассматривать на основе законов Ньютона.

21.1.1.1. Связь показателя преломления с дипольным моментом молекулы

Из теории Максвелла следует(см.16.5.2), что

.

Диэлектрическая проницаемость вещества ε показывает, во сколько раз E₀ - напряженность электрического поля в вакууме больше, чем Е - напряженность поля в среде (см. 9.13.3):

.

Как известно (см. 9.13.3), поле в среде уменьшается за счет возникновения встречного поля Е' , вызванного поляризацией среды. Величина Е' связана с поляризованностью диэлектрика Р (вектором поляризации) следующим соотношением (см. 9.13.3):

.

Таким образом, поле в вакууме E₀ больше, чем в среде на величину Е', т.е.:

.

По определению, поляризованность Р - это сумма дипольных моментов единицы объема среды. Если обозначить через N₀ число молекул среды в единице объема, - наведенный полем световой волны дипольный момент молекулы, то

.

Тогда для ε получим:

.

Так как ε = n²(см. 16.5.2), то

.

 

21.1.1.2. Связь дипольного момента молекулы с напряженностью поля световой волны

Как видно из только что полученной связи n² с p зависимость показателя преломления n от частоты волны ω определяется отношением p/E.

Здесь надо сделать две оговорки. Во-первых, поле, действующее на отдельную молекулу (локальное поле), вообще говоря, не совпадает с величиной среднего (макроскопического) поля в среде E. Мы не будем учитывать в элементарной теории дисперсии это различие, таким образом количественные выводы такой теории могут быть применены только к разреженным газам.

Во-вторых, дипольный момент молекулы p, наведенный полем световой волны E, является функцией от времени, т.е. p = p(t). Так как E = E(t) и фаза колебаний p(t) не совпадает, в общем случае, с фазой колебаний E(t), то для нахождения показателя преломления надо усреднить по времени отношение p(t)/E(t).

Тогда формула для n² приобретет следующий вид:

.

21.1.1.2.1. Простейшая модель атома в поле световой волны

Под действием световой волны совершают колебания только внешние электроны атома, их называют оптическими электронами. Будем считать, что у молекулы (атома) - один оптический электрон. Моделью такого атома будет упругий диполь, дипольный момент которого (см. 9.13.1.1):

.

Оптический электрон будет двигаться под действием квазиупругой силы, силы "трения" и внешней силы, действующей со стороны электрического поля световой волны. Если световая волна поляризованная, то все эти силы будут действовать вдоль одной прямой. Направим вдоль этой прямой ось x, начало координат совместим с положительным зарядом, который будем, в первом приближении, считать неподвижным. Таким образом, мы приходим к модели пружинного маятника, который совершает колебания под действием внешней гармонической силы.

21.1.1.2.2. Уравнение движения электрона и его решение

Уравнение движения, описывающее вынужденные колебания маятника с затуханием было получено нами из второго закона Ньютона в разделе 14.5.5.:

.

Здесь у нас x - координата электрона, ω₀ - собственная частота незатухающих колебаний электрона, β - коэффициент затухания, а

.

E_m - амплитуда световой волны;

ω - циклическая частота световой волны;
m_e- масса электрона,
e - элементарный заряд (e = 1,6 10-19 Кл).

Стационарное решение этого уравнения движения (14.5.6.1):

,

где

 

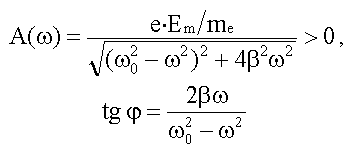
21.1.1.2.3. Проекции дипольного момента и напряженности поля волны на ось x

На следующем рисунке изображен диполь, силы действующие на его полюсы, ось x и вектор электрического поля волны в момент времени t = 0:

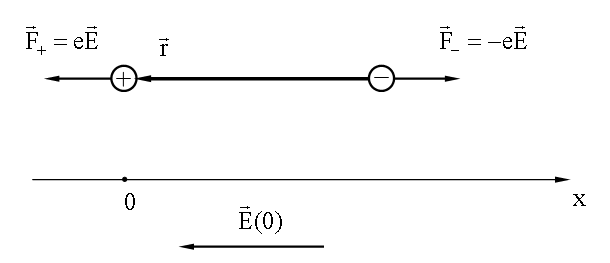
Как видно из рисунка, проекция дипольного момента (21.1.1.2.1) на ось x:

.

Проекция напряженности электрического поля световой волны на ось x:

,

знак минус означает, что в начальный момент времени вектор направлен против оси x. Напомним, что в нашем уравнении движения (21.1.1.2.2) сила, действующая на электрон, при t = 0 имеет положительный знак.

21.1.1.3. Выражение для n²

Подставим в формулу, полученную в (21.1.1.2) для n², выражения p_x(t), N_x(t) с использованием для x(t) решения уравнения движения, записанное в (21.1.1.2.2):

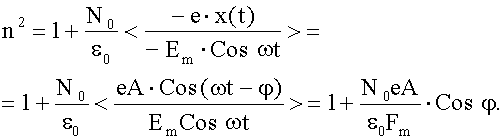
При усреднении по времени дает . Подставляя выражение для амплитуды A-колебаний электрона (из 21.1.1.2.1) получим:

;
.

Сибирская государственная геодезическая академия (СГГА), 2003.