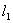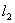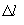Лабораторная работа N 2.
ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ МАЯНИКА ОБЕРБЕКА
ЦЕЛЬ РАБОТЫ: Определить момент инерции маятника Обербека, используя закон сохранения и превращения энергии, и изучить зависимость момента инерции от расположения масс на крестовинах.
ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ
- Маятник Обербека
- Набор грузов.
- Штангенциркуль.
- Секундомер.
ПОДГОТОВКА К РАБОТЕ
По лекциям и списку литературы изучить следующие теоретические вопросы:
- Кинематика вращательного движения
- Момент инерции твердого тела относительно оси вращения. Кинетическая энергия вращения тела.
- Основное уравнение динамики вращательного движения тела.
- Единицы измерения момента инерции. Теорема Штейнера.
СПИСОК ЛИТЕРАТУРЫ
- Савельев И.В. Курс общей физики.
Кн. 1. Механика. — М.: Астрель-Аст, 2002, С. 48-52,154-180 Трофимова Т.Н.
Курс физики. - М.: Высшая школа, 1997,1998, С. 12 -14,
34-40. - Тюшев А.Н. Физика в конспективном изложении. Ч. 1. Механика. Электричество. Магнетизм. - Новосибирск: СГГА, 1999. - С.34 - 42.
ТЕОРИЯ МЕТОДА ИЗМЕРЕНИЙ И ОПИСАНИЕ УСТАНОВКИ
Маятник Обербека (рис. 1) состоит из четырех стержней и двух шкивов различного радиуса, укрепленных на одной горизонтальной оси вращения. По стержням могут перемещаться и закрепляться в нужном положении четыре (по одному на каждом стержне) груза одинаковой массы m0.
На один из шкивов радиуса r1 или R2 наматывается нить, к концу которой крепится платформа с грузом. Пусть m1 - масса платформы, а m2 - масса груза, т.е общая масса: m = m1 + m2.
Если груз m поднять на некоторую высоту h1 и отпустить, то груз придет в движение, а сила натяжения Тн разматывающейся со шкива нити создаст вращающийся момент М. При симметричном расположении грузов на крестовине это будет единственный действующий на систему вращающийся момент.
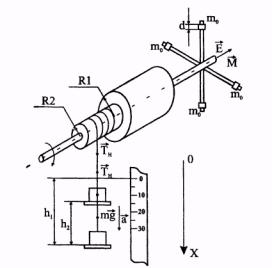
Рис 1.
Пусть в начальный момент времени (t = 0) неподвижная платформа с грузом находится на высоте h1. Полная механическая энергия груза будет определяться потенциальной энергией:
(1)
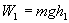
При движении груза потенциальная энергия переходит в кинетическую энергию платформы с грузом и кинетическую энергию вращения маятника В момент времени t1, когда платформа с грузом подходит к нижнему положению, полная энергия системы «маятник Обербека и платформа с грузом» равна:
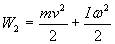
где 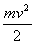 - кинетическая энергия
поступательного движения платформы с грузом;
- кинетическая энергия
поступательного движения платформы с грузом;
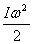 - кинетическая энергия вращающегося
маятника;
- кинетическая энергия вращающегося
маятника;
I - момент инерции маятника относительно оси вращения.
Следует заметить, что в крайнем положении (когда нить полностью размоталась) груз с платформой продолжает двигаться вниз, вызывая деформацию упругой нити. В этом случае кинетическая энергия груза переходит в потенциальную энергию деформации нити. При движении груза вверх потенциальная энергия вновь переходит в кинетическую энергию груза.
При вращении маятника и движении груза действует сила сопротивления воздуха, а в подшипниках на ось вращения действует сила трения. Пусть все эти силы вызывают общий момент силы трения Мтр . Наличие силы трения нарушает закон сохранения механической энергии, так как часть ее переходит во внутреннюю энергию
Работа силы трения при вращении маятника:
(3)
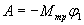
где - 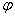 угол поворота махового
колеса при перемещении платформы с грузом на расстояние h1.
угол поворота махового
колеса при перемещении платформы с грузом на расстояние h1.
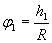
где R - радиус шкива
По закону сохранения общей энергии:
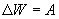
где - 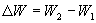 изменение полной энергии
при переходе платформы из верхней точка в нижнюю:
изменение полной энергии
при переходе платформы из верхней точка в нижнюю:
(4)
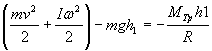
Маятник продолжает вращаться в ту же сторону и поднимает платформу с грузом на высоту h2, причем h2 < h1. При этом система будет обладать энергией:
(5)
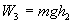
Убыль полной энергии равна работе сил трения при вращении на всем пути движения вниз и вверх:
(6)
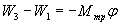
где 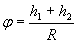 - угол поворота маятника при движении
груза вниз на расстояние h1 и вверх - на h2.
- угол поворота маятника при движении
груза вниз на расстояние h1 и вверх - на h2.
Или, с учетом (5) и (1), выражение (6) запишем:
(7)
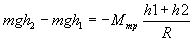
отсюда
(8)
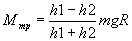
Так как движение маятника с грузом равноускоренное с начальной скоростью, равной нулю, то в низшей точке скорость груза:
(9)
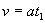
(10)
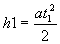
где а - ускорение платформы с грузом,
t1 - время опускания груза. Из уравнений (9) и (10) можно выразить:
(11)
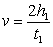
Поскольку нить при движении груза сматывается со шкива без скольжения, линейная
скорость точек, лежащих по поверхности шкива, равна скорости движения груза.
Известно, что угловая скорость вращения связана с линейной скоростью движения
точки по окружности равенством:
(12)
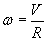
Подставив значение линейной скорости (11) в (12), получим.
(13)
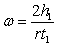
Подставив в уравнение (4) значения Мтр (8), v (11), 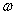 (13),
после преобразований получим расчетную формулу для вычисления момента инерции
маятника Обербека
(13),
после преобразований получим расчетную формулу для вычисления момента инерции
маятника Обербека
(14)
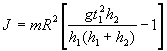
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
- Закрепить грузы на крестовинах на одинаковых расстояниях относительно оси вращения.
- Измерить штангенциркулем радиус шкива, с которого сматывается нить
- Отметить на вертикальной шкале самое низшее положение платформы с грузом-h1.
- Намотать нить на шкив так, чтобы платформа с грузом находилась против нулевого деления шкалы.
- Опустить платформу с грузом, засекая одновременно время.
- Измерить время t1 движения платформы с грузом до полного разматывания нити и высоту h2, на которую поднимется груз.
- Изменить массу 3-5 раз и повторить опыт для каждой массы (пункты 4-6)
- Изменить расстояние расположения грузов на крестовинах
- Повторить опыт (пункты 4-7)
- По формуле (14) вычислить момент инерции маятника
- Вычислить абсолютную погрешность момента инерции I
Результаты измерений и вычислений занести в табл 1
| N п/п |
m |
r |
h1 |
h2 |
t1 |
|
|
|
КОНТРОЛЬНЫЕ ВОПРОСЫ
- Объяснить зависимость момента
инерции маятника от расположения
грузов на крестовине - Каким будет движение маятника при отсутствии трения?
- Вывести расчетную формулу для момента инерции ?
- Действует ли этот закон в данном эксперименте?