ОПРЕДЕЛЕНИЕ СКОРОСТИ ПУЛИ ПРИ ПОМОЩИ БАЛЛИСТИЧЕСКОГО МАЯТНИКА
ЦЕЛЬ РАБОТЫ: Определить скорость пули и работу деформации, используя законы неупругого соударения тел.
ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ
ПОДГОТОВКА К РАБОТЕ
По лекциям и списку литературы изучить следующие вопросы:
СПИСОК ЛИТЕРАТУРЫ
ТЕОРИЯ МЕТОДА ИЗМЕРЕНИЙ И ОПИСАНИЕ УСТАНОВКИ
В данной работе для определения скорости полета пули используется баллистический маятник.
Баллистический маятник представляет собой цилиндр массой М, подвешенный на длинных нитях. Цилиндр маятника заполнен пластилином. К нему прикреплена стрелка для отсчета его смещения по горизонтальной шкале.
В работе рассматриваются абсолютно неупругий удар и многократные неупругие удары пули внутри цилиндра. При абсолютно неупругом ударе пуля двигается острым концом в направлении цилиндра и после удара застревает в пластилине. Если пуля двигается тупым концом к цилиндру, то она испытывает многократные столкновения внутри цилиндра, не вылетая из него.
Если время соударений пули с маятником мало по сравнению с периодом колебания маятника, то маятник не успевает заметно отклониться от исходного положения за время соударений. Это значит, что во время ударов не возникает составляющая силы тяжести, стремящейся вернуть маятник в исходное положение. Поэтому в таком случае действие силы тяжести уравновешивается силой упругости нитей, и систему «пуля - маятник» можно рассматривать как замкнутую и применять к ней закон сохранения импульса.
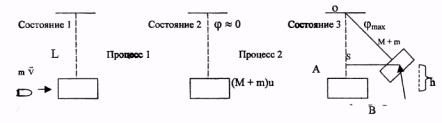
После выстрела из пружинного пистолета пуля массой т, летящая со скоростью v, попадает в цилиндр. Цилиндр маятника, висевший неподвижно, получает вследствие удара пули некоторую скорость и отклоняется от положения равновесия. Законы сохранения импульса и энергии позволяют связать скорость пули v с отклонением маятника и найти скорость пули по величине отклонения. На рис. 1 изображена система «пуля - маятник» в трех важных состояниях:
Состояние 1 - пуля вылетела из пистолета, но еще не долетела до мишени. Мишень неподвижна.
Состояние 2 - пуля попала в мишень, мишень вместе с пулей начали движение со скоростью u, отклонение маятника приблизительно равно нулю.
Состояние 3 - маятник отклонился на максимальный угол и сместился по горизонтали на расстояние S, которое измеряем в работе. При отклонении маятника по горизонтали на расстояние S маятник поднимается на высоту h.
 |
 |
 |
 |
 |
 |
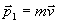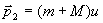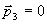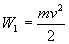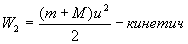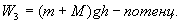В процессе перехода системы «пуля - маятник» из первого состояния во второе (процесс 1) сохраняется горизонтальная составляющая импульса системы. Таким образом, полный импульс системы до попадания пули в маятник:
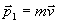
будет равен полному импульсу системы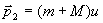
сразу после попадания в маятник:
(1)
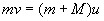
Полная механическая энергия системы в процессе 1 не сохраняется, так как при движении пули в пластилине или же при многократных неупругих ударах действуют неконсервативные силы. Убыль механической энергии равна работе деформации:
(2)
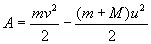
В процессе 2 (перехода из второго состояния в третье) работу совершает лишь консервативная сила тяжести, поэтому к процессу 2 можно применить закон сохранения полной механической энергии:
(3)
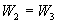
здесь
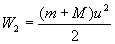
полная механическая энергия системы пуля-маятник» в состоянии 2:
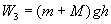- полная механическая энергия
системы «пуля - маятник» -в состоянии 3.
Подставляя значения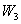 
в (3),
получим:
(4)
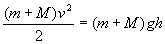
Эта формула дает связь между параметрами второго и третьего состояний. После сокращения на (m + М) и очевидных преобразований имеем:
(5)
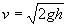
Таким образом, равенства (1) и (3) связывают между собой первое и третье состояние. Исключая из них промежуточный параметр и, получаем:
6)
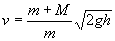
Высоту подъема цилиндра h выразим через горизонтальное смещение S и длину маятника L, которые измеряются в работе (см. состояние 3). В треугольнике ОАВ OA = L-h, OB = L,
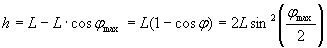
При L >> S можно считать, что угол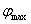 
мал, т.е.
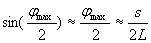
Тогда
(7)
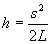
а скорость после удара:
(8)
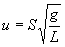
Подставив (8) в (2) и (7) в (6), получим рабочие формулы скорости пули и работы деформации А:
(9)
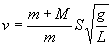
(10)
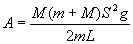
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Отметить по шкале положение стрелки «n0» при неподвижном цилиндре.
1. Сжать пружину пистолета и вложить пулю тупым концом в ствол.
2. Произвести выстрел из пистолета по маятнику. Отсчитать положение стрелки при максимальном отбросе «n». Найти отклонение цилиндра S = n-n0
3. Опыт повторить не менее трех раз. При повторных выстрелах цилиндр необходимо возвратить в начальное положение (т.е. выстрел производить по неподвижному цилиндру). Необходимо ориентировать баллистический маятник горизонтально и так, чтобы пуля попадала в середину маятника.
4. Повторить пункты 1 - 3 с пулей той же массы, вкладывая пулю острым концом в ствол пружинного пистолета. Следить, чтобы пуля после выстрела попадала в середину цилиндра и после многократного столкновения не вылетала из маятника.
5. Вычислить для двух случаев скорость пули до удара и работу деформации А при ударе пули и цилиндра.
6. Вычислить погрешности измерений ΔV и ΔA.
7. Записатьокончательныйрезультат в виде:
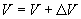
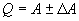
Данные измерений и вычислений занести в табл. 1
Таблица1
| N п/п |
M |
m |
L |
n0 |
n |
S |
v |
ΔVi |
|
A |
|
|
Массы цилиндра и пуль, длина нитей указаны на установке.
КОНТРОЛЬНЫЕ ВОПРОСЫ
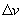и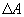 
.
