При выполнении лабораторной работы осуществляются два последовательных этапа:
а) измерения в ходе опытов;
б) вычисление и обработка результатов измерений.
Измерением какой-либо физической величины называется операция, в результате которой мы узнаем, во сколько раз измеряемая величина больше (или меньше) соответствующей величины, принятой за эталон.
Различают два вида измерений: прямое и косвенное.
Прямыми называют такие измерения, при которых измеряемая величина определяется каким-либо прибором. Известно, что непосредственно могут быть измерены лишь немногие физические величины, такие, как длина, масса тела, промежутки времени, температура и др. Остальные величины мы определяем с помощью вычислений, пользуясь функциональными связями между физическими величинами, найденными прямыми измерениями. Таким образом, если физическая величина определяется на основании формулы, то такое измерение называется косвенным.
При оценке измерений следует исходить из того, что все измерения являются приближенными с ограниченной точностью. Приближенные величины можно разделить на три типа:
- Математические приближенные величины:
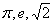, логарифмы чисел
и т.п., приводимые в специальных таблицах. Они могут быть взяты практически
с любой точностью. При вычислениях берут такие их значения, которые превышают
на порядок точность других рассматриваемых величин. - Физические постоянные.Постоянные (плотность, коэффициент расширения, удельное сопротивление и т.п.) получены в результате точных измерений с малой погрешностью, которую необходимо учитывать лишь при очень точном измерении других связанных с ними величин. Фундаментальные, или мировые, постоянные (гравитационная постоянная, число Авогадро, постоянная Больцмана, постоянная Планка, скорость света и др.) определяются с максимально возможной для данного времени точностью измерений. Погрешность измерений мировых постоянных обычно намного меньше погрешности измерений рядовых постоянных, поэтому ею, как правило, пренебрегают.
- Данные обычных лабораторных измерений. Точность их ниже, чем точность величин первого и второго типа, указанных выше. Ошибки, допущенные при измерениях, делятся на систематические, случайные и грубые (просчеты).
- Систематические ошибки могут быть обусловлены методом измерений. Например, определение ускорения свободного падения g из периода колебаний математического маятника по формуле:
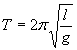
является приближенным, прежде всего, потому, что формула для вычисления приближенная. Более точна формула
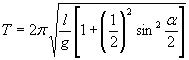
Систематическая ошибка может вноситься измерительными приборами или инструментом (за счет смещения нуля, трения в подвижной системе прибора и т.д.). Кроме того, каждый прибор имеет определенный класс точности показаний (ОД; 0,2; 0,5; 1,0; 1,5; 2,5; 4,0). Это означает, что максимальные расхождения деления его шкалы с истинными значениями, или погрешность измерений, может составить для отдельных измерений соответственно: 0,1; 0,2; ... 4% от наибольшего значения величины, измеряемой по шкале прибора. Величина систематической ошибки одинакова во всех измерениях, проводимых одним и тем же методом с помощью одних и тех же приборов, и не уменьшается с увеличением числа измерений.
Для уменьшения влияния систематических ошибок требуются тщательный анализ метода измерений, проверка показаний приборов по другим, более точным и надежным приборам и соответствующее их исправление, учет постоянно действующих внешних влияний.
Грубые ошибки (просчеты) вызываются неверными отсчетами или неправильными записями показаний приборов, просчетами при вычислениях, являются следствием недостатка внимания и усталости экспериментатора.
Для их выявления нужно анализировать результаты сразу после их измерения и вычисления. Если результат измерения в эксперименте значительно отличается от результатов других измерений, то его следует исключить из рассмотрения и провести повторные измерения. Если при расчетах получен результат, значительно отличающийся от других, то необходимо повторить расчеты.
Случайные ошибки являются неизбежным следствием любых измерений и обусловлены:
а) неточностью отсчетов по шкале приборов и инструментов;
б) не идентичностью условий повторных измерений;
в) беспорядочными изменениями внешних условий (температуры, давления, силового поля и т.д.), которые невозможно контролировать;
г) всеми другими воздействиями на измерения, причины которых нам неизвестны. Величину случайной погрешности можно свести к минимуму путем многократного повторения эксперимента и соответствующей математической обработки полученных результатов.
Случайные ошибки подчиняются определенной закономерности. Функция распределения случайных погрешностей впервые была определена Гауссом, который создал теорию случайных погрешностей, так называемый закон нормального распределения случайных погрешностей.
При обработке результатов измерений при малом их количестве широко используется метод Стьюдента. Следует отметить, что распределение Стьюдента при достаточно большом количестве измерений переходит в нормальное распределение.
Результаты n отдельных измерений некоторой величины х за счет случайных ошибок дают различные значения x1, х2, x3, ... хn. При измерениях одинаковой точности наиболее близким к истинному значению является среднее арифметическое значение всех n-измерений, так как случайные ошибки могут быть разного знака и при сложении частично компенсируют друг друга. Среднее арифметическое n отдельных измерений:
(1)
Cтепень приближения среднего значения х к истинному значению
измеряемой величины можно выразить через так называемый доверительный интервал
с некоторой заданной
надежностью 
. Надежностью
измерения называется вероятность того, что измеренная величина попадает в
указанный доверительный интервал. Надежность или доверительная вероятность
выражается либо в долях единицы, либо в процентах.
Погрешность среднего арифметического n измерений, или средняя квадратичная ошибка, определяется следующим выражением:
(2)
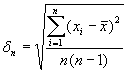
Задача обработки результатов состоит в том, чтобы определить доверительный интервал Δх:
(3)
где 
- коэффициент Стьюдента, численное значение которого для различных 
и n приведено в табл. 1. Таким образом, устанавливается следующий
порядок обработки результатов:
а) находим приближенное среднее арифметическое по формуле (1);
б) вычисляем приближенную погрешность среднего арифметического по формуле (2);
в) исходя из количества измерений и по заданной надежности, из табл. 1 на
ходим коэффициент ;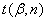
г) находим доверительный интервал по формуле (3);
д) окончательный результат, записываем в виде;
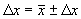
Таблица 1.
Таблица коэффициентов Стьюдента.
