Выполнение арифметических операций над числами в некоторой позиционной системе счисления с основанием X аналогично выполнению операций над числами в десятичной системе счисления, при этом также учитывают, что X единиц младшего разряда составляют одну единицу старшего разряда:

9₁₀ + 1 = 10₁₀, F₁₆ + 1 = 10₁₆ , 7₈ + 1 = 10₈, 1₂ + 1 = 10₂.

При сложении двух однозначных чисел (в сумме не меньших основания) можно второе слагаемое представить суммой двух чисел (одно из которых дополняет первое слагаемое до основания X).

Примеры:

• 7₁₀ + 7₁₀ = 7₁₀ + (3₁₀ + 4₁₀) = (7₁₀ + 3₁₀) + 4₁₀ = 10₁₀ + 4₁₀ = 14₁₀
;

• B₁₆ + C₁₆ = B₁₆ + (5₁₆ + 7₁₆) = (B₁₆ + 5₁₆) + 7₁₆ = 10₁₆ + 7₁₆ = 17₁₆ (так как B₁₆ = 11₁₀, C₁₆ = 12₁₀);

• 3₈ + 9₈ = 3₈ + (5₈ + 4₈) = (3₈ + 5₈) + 4₈ = 10₈ + 4₈ = 14₈;


• 1₂ + 1₂ = 1₂ + (1₂ + 0₂) = (1₂ + 1₂) + 0₂ = (10₂) + 0₂ = 10₂.

Аналогичным образом можно выполнить операцию сложения над многозначными числами, например, как известно, чтобы в десятичной системе счисления найти сумму двух чисел 525 + 768, складывают отдельно соответствующие разряды, при этом полученные 10 единиц младшего разряда преобразуют в единицу старшего разряда (прибавляют к цифре старшего разряда).

Также можно выполнить операции сложения над числами с основанием X.

Например, B25₁₆ + 79C₁₆, 523₈ + 716₈, 1101₂ + 1001₂.

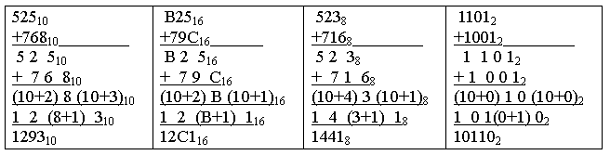
Таким образом,

B25₁₆ + 79C₁₆ = 12C1₁₆, 523₈ + 716₈ = 1441₈, 1101₂ + 1001₂ = 10110₂.

Для проверки правильности выполнения операций сложения можно перевести каждое число в десятичную систему счисления. Попробуйте выполнить эту проверку самостоятельно.

Вычитание чисел с основанием X можно выполнять так же, как и в десятичной системе счисления, при этом учитывают, что:

10₁₀ – 1 = 9₁₀, 10₁₆ – 1 = F₁₆, 10₈ – 1 = 7₈, 10₂ – 1 = 1₂.

Например, как известно, чтобы в десятичной системе счисления найти разность двух чисел 251 – 128, вычитают отдельно соответствующие разряды и, при необходимости, в вычитаемом единицу старшего разряда преобразуют в 10 единиц и добавляют к младшему разряду.

Также можно выполнить операции вычитания над числами с основанием X.

Например, 2C1₁₆ – 134₁₆, 362₈ – 124₈, 1110₂ – 1001₂.

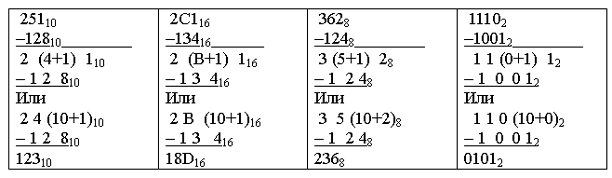
Таким образом,

2C1₁₆ – 134₁₆ = 18D₁₆, 362₈ – 124₈ = 236₈, 1110₂ – 1001₂ = 101₂.

Для проверки правильности выполнения операций вычитания можно перевести каждое число в десятичную систему счисления.

Попробуйте выполнить эту проверку самостоятельно.

Умножение чисел в системе счисления с основанием X можно выполнять так же, как и в десятичной системе счисления, учитывая, что: A_X · 2 = A_X + A_X, A_X · 3 = A_X + A_X + A_X и т. д.

Например:

Таким образом,

24₁₆· 35₁₆ = 774₁₆, 25₈· 23₈ = 617₈, 1001₂· 101₂ = 101101₂.

Для проверки правильности выполнения операций умножения можно перевести каждое число в десятичную систему счисления. Попробуйте выполнить эту проверку самостоятельно.

Деление чисел в системе счисления с основанием X можно выполнять так же, как и в десятичной системе счисления – углом, но для наглядности эту операцию можно представить, например, следующим образом:

642₁₀ : 12₁₀.

Выделяем старшие разряды (десятки), которые можно делить на 12:
64₁₀ : 12₁₀ = 5 единиц старшего разряда (остаток 4 единицы старшего разряда).

Преобразуем остаток (4 единицы старшего разряда) в 40 единиц следующего младшего разряда и добавим 2 единицы младшего разряда (числа 642) и продолжим деление:

42 : 12 = 3 единицы (остаток 6 единиц).

Вновь преобразуем остаток (6 единиц) в 60 единиц следующего младшего разряда (то есть в десятые доли) и продолжим деление:

60 : 12 = 5 десятых (остаток 0).

Так как остаток равен нулю, то деление прекращаем и записываем результат

642₁₀ : 12₁₀ = 53,5₁₀.

Аналогичным образом можно выполнить операцию деления над числами с основанием X, например,

1202₈ : 14₈, 282₁₆ : C₁₆, 1111₂ : 110₂.

Выполним операцию 1202₈ : 14₈. Вначале выделяем старшие разряды (120), которые можно делить на 14₈:

120₈ : 14₈ = 6 единиц старшего разряда (остаток 10₈ единиц старшего разряда).

Преобразуем остаток (10₈ единиц старшего разряда) в 100 единиц следующего младшего разряда и добавим 2 единицы младшего разряда (числа 1202₈) и продолжим деление:

102₈ : 14₈ = 5 единиц (остаток 6 единиц).

Вновь преобразуем остаток (6 единиц) в 60 единиц следующего младшего разряда и продолжим деление:

60₈ : 14₈ = 4 доли (остаток 0).

Так как остаток равен нулю, то деление прекращаем и записываем результат

1202₈ : 14₈ = 65,4₈.

Выполним операцию 282₁₆ : C₁₆.

Вначале выделяем старшие разряды (28), которые можно делить на C₁₆:

28₁₆ : C₁₆ = 3 единицы старшего разряда (остаток 4 единицы старшего разряда).

Преобразуем остаток (4 единицы старшего разряда) в 40 единиц следующего младшего разряда и добавим 2 единицы младшего разряда (числа 282₁₆) и продолжим деление:

42₁₆ : C₁₆ = 5 единиц (остаток 6 единиц).

Вновь преобразуем остаток (6 единиц) в 60 единиц следующего младшего разряда и продолжим деление:

60₁₆ : C₁₆ = 8 долей (остаток 0).

Так как остаток равен нулю, то деление прекращаем и записываем результат 282₁₆ : C₁₆ = 35,8₁₆.

Выполним операцию 1111₂ : 110₂.

Вначале выделяем старшие разряды (111), которые можно делить на 110₂:

111₂ : 110₂ = 1 единица старшего разряда (остаток 1 единица старшего разряда).

Преобразуем остаток (1 единицу старшего разряда) в 10 единиц следующего младшего разряда и добавим 1 единицу младшего разряда (числа 1111₂) и продолжим деление:

11₂ : 110₂ = 0 единиц (остаток 11 единиц).

Вновь преобразуем остаток (11 единиц) в 110 единиц следующего младшего разряда и продолжим деление:

110₂ : 110₂ = 1 доля (остаток 0).

Так как остаток равен нулю, то деление прекращаем и записываем результат

1111 : 110₂ = 10,12.

Таким образом,

282₁₆: C1₁₆ = 35,8₁₆, 1202₈ : 14₈ = 65,4₈, 1111₂ : 110₂ = 10,1₂.

Для проверки правильности выполнения операций деления можно перевести каждое число в десятичную систему счисления. Попробуйте выполнить эту проверку самостоятельно.