Начертательная геометрия

2.3 Плоскость

Основные положения:

горизонталь и фронталь являются главными линиями плоскости (рис. 26);

Рис. 26. Главные линии плоскости

если точка принадлежит плоскости, то она лежит на прямой, принадлежащей данной плоскости;
прямая параллельна плоскости, если она параллельна какой-либо прямой, принадлежащей этой плоскости; на эпюре одноименные проекции данной прямой и прямой, принадлежащей плоскости, параллельны между собой;

если прямая перпендикулярна плоскости, то её горизонтальная проекция перпендикулярна горизонтальной проекции горизонтали плоскости, а фронтальная - перпендикулярна фронтальной проекции фронтали (рис. 27);

Рис. 27. Эпюр прямой, перпендикулярной плоскости

плоскость, перпендикулярная к одной из плоскостей проекций, называется проецирующей; на комплексном чертеже одна из её проекций будет изображаться в виде прямой линии на плоскости проекций, перпендикулярной к проецирующей плоскости; линия пересечения плоскости с плоскостью проекций называется следом плоскости;
плоскость, параллельная одной из плоскостей проекций, называется плоскостью уровня; такая плоскость перпендикулярна одновременно к двум плоскостям проекций; на комплексном чертеже одна из её проекций будет изображаться в виде прямой линии, параллельной оси проекций, а другая проекция на плоскости проекций, параллельной плоскости уровня, будет изображать натуральную величину плоскости;
плоскости параллельны, если проекции двух пересекающихся прямых одной плоскости параллельны проекциям двух пересекающихся прямых другой плоскости;
если плоскость проходит через прямую, перпендикулярную к другой плоскости, то эти плоскости взаимно перпендикулярны;
для построения точки пересечения прямой с плоскостью надо выполнить следующее (рис. 28):

Рис. 28. Решение задачи в пространстве

а) через данную прямую l провести вспомогательную проецирующую плоскость β;

б) построить линию пересечения (1-2) данной плоскости α и вспомогательной β;

в) определить точку K - точку пересечения прямых, данной l и построенной (1-2).

На комплексном чертеже (рис. 29) в качестве проецирующей плоскости выберем фронтально проецирующую плоскость β, фронтальная проекция которой β "П₂ и проходит через фронтальную проекцию прямой l″.

Рис. 29. Нахождение точки встречи

Найдем линию пересечения (1-2) этой проецирующей плоскости с плоскостью треугольника АВC, зная, что стороны АC и BC пересекаются с плоскостью β в точках 1 и 2. По линиям связи определяем горизонтальные проекции точек 1′ и 2′. На пересечении горизонтальных проекций прямой l′ и построенной прямой (1′-2′) находим горизонтальную проекцию точки пересечения прямой l с плоскостью треугольника АВC - K′. По линии связи находим фронтальную проекцию K″. Видимость прямой и плоскости относительно плоскостей проекций определяем методом конкурирующих точек.

Рассматривая пару точек 1 и 3 , конкурирующих относительно фронтальной плоскости проекций П₂, видим, что точка 1 ближе к нам. Точка 1 принадлежит прямой АC, следовательно прямая АC закрывает прямую l относительно плоскости П₂ и её часть 3K будет невидима, а часть K4 - видима. Аналогично, используя конкурирующие точки 4 и 5 , определим видимость прямой и плоскости относительно горизонтальной плоскости проекций П₁.

Для определения линии пересечения двух плоскостей α и β общего положения необходимо (рис. 30):
а) данные плоскости пересечь третьей плоскостью - посредником γ;

б) определить линии пересечения плоскости γ с плоскостями α и β (1-2, 3-4);

в) определить точку пересечения полученных линий - А;

г) для определения второй точки пересечения B обе данные плоскости пересекают еще одной плоскостью – посредником - δ.

Рис. 30. Решение задачи в пространстве

В качестве плоскости - посредника выбирают плоскости уровня или проецирующие.

Плоскости уровня обычно применяют тогда, когда проекции прямых, задающие плоскости на чертеже, не пересекаются.

Для нахождения линии пересечения плоскостей, заданных двумя треугольниками, применяют метод нахождения точки пересечения прямой с плоскостью.

В заданных плоскостях (рис. 31) выделяют две прямые АВ и EF и находят точки пересечения их с другой плоскостью, используя фронтально проецирующие плоскости Ф₁ и Ф₂.

Рис. 31. Построение линии пересечения треугольников

Сначала находят точку пересечения прямой АВ с плоскостью треугольника DEF, т.е. первую точку M искомой линии пересечения плоскостей. Точка M находится на пересечении горизонтальных проекций прямой АВ и линии 1-2.

Затем аналогично находят точку пересечения прямой FE с плоскостью треугольника АВC, т.е. вторую точку N линии пересечения. Точка N находится на пересечении горизонтальных проекций прямой FE и линии 3-4. Точки M и N соединяют прямой, получая искомую линию пересечения треугольников. Видимость пересекающихся плоскостей относительно плоскости П₂ определяют по конкурирующим точкам 1 и 5 , а относительно плоскости П₁ - по конкурирующим точкам 6 и 7 .

ЗАДАЧИ

Задача 23

Построить недостающие проекции прямой l и точек M и N , принадлежащих плоскости Δ АВC.

Задача 24

По данной горизонтальной проекции плоского пятиугольника АВCDE и фронтальной проекции его сторон АВ и АE построить фронтальную проекцию пятиугольника. Координаты:
А(75,40,30), B(50,20,65), C(20,20,?), D(0,55,?), E(35,65,15).

Задача 25

Через точку А провести в плоскости α горизонталь, а через точку B- фронталь.

Задача 26

В плоскости ΔАВC построить точку, удаленную от плоскости проекций П₁ на 20 мм и от плоскости проекций П₂
на 15 мм.

Задача 27

Через прямую a провести горизонтально проецирующую плоскость α (a||c) и фронтально проецирующую плоскость β (a||c).

Задача 28

Определить, как расположена прямая относительно плоскости?

Задача 29

Через (•) А провести прямую, параллельную плоскости α (mk).

Задача 30

Через (•) А провести прямую, перпендикулярную к прямым m и k (m k).

Задача 31

Задать плоскость α, проходящую через (•)M и параллельную плоскости:

а) β (k||l),

б) β (ΔАВC.)

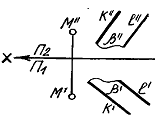
а)

б)

Задача 32

Найти точку встречи прямой m с плоскостью ΔАВC. Определить видимость прямой относительно плоскости.

Задача 33

Через (•) А провести плоскость α, перпендикулярную к прямой a.

Задача 34

Определить проекции расстояния от точки А до прямой a.

Задача 35

Построить проекции расстояния от точки D до плоскости ΔАВC.