ФИЗИКА в конспективном изложении. Часть 3

Содержание Назад Далее

 

ОСНОВЫ МОЛЕКУЛЯРНОЙ ФИЗИКИ И ТЕРМОДИНАМИКИ

25. Элементы физической кинетики

Статистическая физика (23) и термодинамика (24), каждая своим методом, изучает равновесные состояния физических систем и обратимые процессы, происходящие в них.

Физическая кинетика и термодинамика неравновесных процессов, каждая своим методом, изучает процессы в неравновесных системах.

Термодинамика неравновесных процессов дает общую феноменологическую теорию макроскопического описания неравновесных процессов.

В отличие от термодинамики неравновесных процессов физическая кинетика исходит из представлений о молекулярном строении рассматриваемых физических систем и силах взаимодействия между молекулами.

Мы в этом разделе кратко рассмотрим простейшие неравновесные процессы - диффузию, теплопроводность и вязкость, проходящие в идеальных газах. Рассмотрим также явление электропроводности в металлах. Наше рассмотрение будет приближенным, так как мы будем использовать самую простую модель этих явлений. Благодаря простоте используемой модели мы надеемся дать ясное представление о физической сути происходящих явлений. Выяснится и принципиальный недостаток классической модели (в случае с электропроводностью).

25.1. Эффективный диаметр молекул

Как мы знаем из основных положений молекулярно-кинетической теории (22.1.5) молекулы на близких расстояниях отталкиваются друг от друга.

Движение двух молекул, летящих навстречу друг другу, проще проанализировать, если использовать закон сохранения механической энергии (5.8) применительно к этим молекулам. Потенциальная энергия взаимодействия двух молекул W_n(r) изображена на следующем графике. На расстоянии r₀ потенциальная энергия достигает минимума, а силы взаимодействия обращаются в ноль (22.1.9).

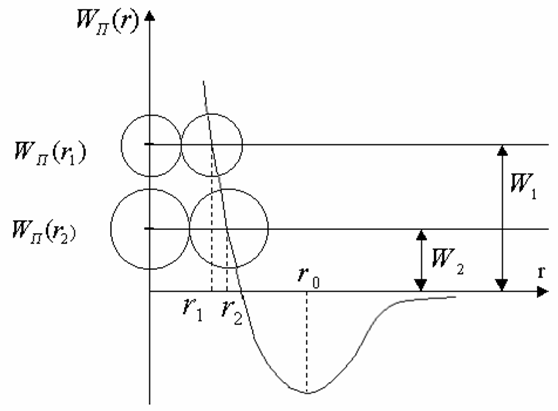
При большом расстоянии между молекулами (r >> r₀) W_n = 0, в этом случае их полная энергия W является суммой их кинетических энергий. При сближении молекул сначала, до точки r₀, действуют силы притяжения, затем - силы отталкивания. За счет работы сил отталкивания кинетическая энергия молекул уменьшается, и при некотором расстоянии молекулы на мгновение останавливаются.

В этот момент времени полная энергия молекул W равна потенциальной энергии их взаимодействия W_n(r) . Ясно, что с увеличением полной энергии минимальное расстояние, на которое могут сблизиться молекулы, уменьшается. Так на приведенном рисунке полная энергия W₁ больше полной энергии W₂. Поэтому расстояние r₁, на которое могут сблизиться  молекулы с энергией W₁, меньше, чем расстояние r₂, на которое сближаются молекулы с энергией W₂.

В случае соударения двух одинаковых шаров минимальное расстояние между центрами шаров равно их диаметру. Поэтому эффективным диаметром молекулы d называют минимальное расстояние, на которое сближаются при соударении центры двух молекул.

Ясно, что эффективный диаметр молекулы зависит от скорости их сближения (кинетической энергии на большом расстоянии), а значит - от температуры (22.2.7).

25.2. Средняя длина свободного пробега

Будем считать молекулы шарами с диаметром d, равным эффективному диаметру (25.1). Будем также считать, что все молекулы движутся в случайных направлениях с одинаковой скоростью, равной средней скорости <v> (23.4.2.5). Тогда средняя длина свободного пробега λ будет связана со средней скоростью молекул <v> простой формулой:

λ = <v>τ,

здесь τ - среднее время свободного пробега, т.е. среднее время, в течение которого молекула движется между двумя последовательными соударениями. Иными словами - за время τ молекула в среднем испытывает одно столкновение.

25.2.1. Формула для τ - среднего времени свободного пробега

Величина τ зависит от числа молекул в единице объема n (концентрации), их эффективного диаметра d и от средней относительной скорости v_отн сталкивающихся молекул.

Средняя относительная скорость движения молекул v_отн больше, чем их средняя скорость <v>. Можно показать, что:

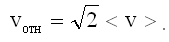
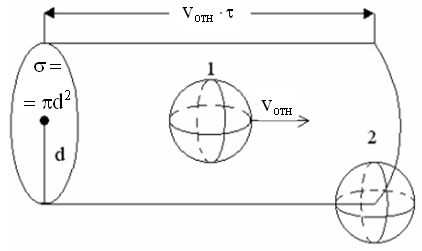
На рисунке проиллюстрирован процесс столкновения двух молекул в системе отсчета, где молекула 2 покоится. Молекула 1 может столкнуться с молекулой 2, если центр молекулы 2 расположен от линии движения молекулы 1 не дальше чем d - эффективный диаметр молекул. Это значит, что в объеме изображенного на рисунке цилиндра в среднем должна находиться одна молекула. Обозначим площадь основания этого цилиндра буквой σ. Величина σ называется полным сечением столкновения двух молекул. Объем будет равен σ·(v_отн·τ). Умножив этот объем на концентрацию n, мы получим число молекул N в объеме изображенного цилиндра, которое, как сказано выше, должно быть равно единице (одно столкновение за время τ!), т.е.

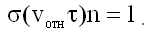
Откуда

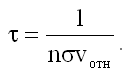
Подставляя сюда , получим:

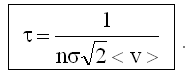
25.2.2. Связь длины свободного пробега λ с концентрацией молекул n и полным сечением столкновения σ

Подставив в формулу для λ из (25.2) величину τ из (25.2.1), получим формулу, связывающую длину свободного пробега с концентрацией молекул и полным сечением столкновения σ:

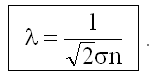
Напомним, что а d - эффективный диаметр молекулы (25.1), он уменьшается с ростом температуры.

25.2.3. Связь λ с давлением p и температурой T

Так как p = nkT  (22.2.5), то из (25.2.2) для λ получим:

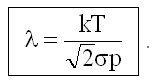
Оценим λ для газа, находящегося при нормальных условиях:
(p = 1 атм ≈10⁵ Па, T = 0╟С = 273 К).

Примем, что эффективный диаметр молекул d ≈ 2·10^-10 м, тогда

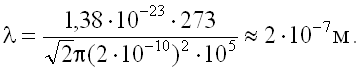
Таким образом λ >> d, т.е. при обычных условиях молекула пролетает относительно большое расстояние прежде, чем столкнется с другой молекулой.

25.3. Диффузия

Диффузией называется самопроизвольное выравнивание концентрации смеси различных веществ, происходящее вследствие теплового движения частиц вещества.

Диффузия происходит в направлении уменьшения концентрации вещества и ведет к равномерному распределению его по занимаемому объему.

25.3.1. Плотность потока молекул j

Плотность потока молекул j - это отношение числа молекул dN, прошедших за время dt через площадку , расположенную перпендикулярно движению молекул, к dt и , т.е.:

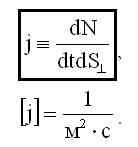
25.3.2. Закон Фика

Опытным путем установлено, что в случае, когда n = n(z):

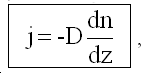
здесь D - коэффициент диффузии, его размерность

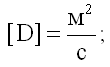
 - градиент концентрации молекул (при n = n(z)).

Приведенная связь плотности потока молекул с градиентом концентрации носит название закона Фика. Здесь записан закон Фика для случая, когда концентрация n зависит только от одной пространственной переменной z.

25.3.3. Самодиффузия в газах

Рассмотрим газ, состоящий из двух почти одинаковых, но отличающихся друг от друга компонент (например, ядра атомов у одной компоненты являются радиоактивными).

Пусть концентрация n₁ первой компоненты зависит от одной координаты, скажем

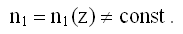
При этом полная концентрация молекул остается неизменной, т.е.

n = n₁ + n₂ = const

n₂ - концентрация второй компоненты. Она, как и n₁, тоже не будет постоянной.

Вследствие теплового движения молекул будет происходить выравнивание их концентраций, т.е. диффузия первой и второй компонент газа. Так как компоненты газа почти одинаковы, то такая диффузия называется самодиффузией.

Изобразим площадку dS, расположенную перпендикулярно оси z, и найдем плотность потока молекул, пересекающих эту площадку.

Будем считать, как и в (22.2.6), что в направлении оси z со средней скоростью <v> движется 1/6 часть всех молекул. Тогда через площадку dS за время dt пройдет dN₊  молекул снизу:

и  dN_-- молекул сверху:

В выражениях для dN₊  и dN_- концентрации n₁ взяты на расстояниях ±λ от площадки dS, т.к. в среднем последнее соударение молекулы испытывали на расстоянии средней длины свободного пробега λ (25.2).

Результирующее число молекул dN, прошедших через площадку dS за время dt, будет:

Стоящее в квадратных скобках приращение величины n₁ на расстоянии 2λ можно заменить ее дифференциалом:

Это можно сделать, если .

С учетом (25.3.1) получим следующее выражение для плотности диффузионного потока молекул:

25.3.4. Коэффициент самодиффузии в газах

Сравнивая полученную в (25.3.3) формулу для плотности диффузионного потока молекул с законом Фика (25.3.2), получим для коэффициента диффузии следующее выражение:

Ввиду упрощенного рассмотрения диффузии, величине численного коэффициента 1/3 нельзя придавать серьезного значения, но зависимость D от <v> и λ даже при приближенном рассмотрении получилась верная.

25.4. Теплопроводность

Теплопроводностью называется перенос теплоты от нагретых частей тела к менее нагретым, приводящий к выравниванию температуры.

При теплопроводности перенос тепловой энергии осуществляется в результате непосредственного столкновения молекул с отличающейся средней энергией теплового движения.

25.4.1. Плотность теплового потока

Плотность теплового потока j_q - это отношение количества теплоты δQ, переданного вследствие теплопроводности за время dt через площадку , расположенную перпендикулярно направлению переноса тепловой энергии к dt и , т.е.:

 

Сибирская государственная геодезическая академия (СГГА), 2006.