Физика в конспективном изложении. Часть III.

	ФИЗИКА в конспективном изложении. Часть 3

Содержание	Назад	Далее

ОСНОВЫ МОЛЕКУЛЯРНОЙ ФИЗИКИ И ТЕРМОДИНАМИКИ

25. Элементы физической кинетики

25.4.2. Закон Фурье

Опытным путем установлено, что

здесь χ- коэффициент теплопроводности, его размерность

dT/dz - градиент температуры.

Приведенная связь плотности теплового потока с градиентом температуры носит название закона Фурье. Здесь написан закон Фурье для случая, когда температура T зависит только от одной координаты - z.

25.4.3. Теплопроводность газов

Пусть температура газа зависит от одной координаты, скажем, z, т.е.: T = T(z) ≠ const.

Изобразим площадку dS, расположенную перпендикулярно оси z, и найдем плотность теплового потока через эту площадку.

Средняя энергия теплового движения молекулы, пересекающей площадку dS снизу:

см. (22.2.9).

Аналогично для молекулы, пересекающей площадку dS сверху:

Температуры и определяющие средние энергии молекул, взяты на расстояниях ±λ от площадки (как и концентрация n₁ в (25.3.3)).

Число молекул, пересекающих площадку снизу вверх и сверху вниз одинаково и, аналогично (25.3.3), дается выражением:

Количество теплоты δQ, переносимое за время dt через площадку ,

Заменим на дифференциал приращение температуры на расстоянии 2λ:

Это можно сделать, если

т.е. при достаточно малом градиенте температуры.

С учетом (25.4.1) получим следующее выражение для плотности теплового потока:

25.4.4. Коэффициент теплопроводности газов

Сравнивая предыдущую формулу с законом Фурье (25.4.2), получим для коэффициента теплопроводности χ следующее выражение:

Величина, стоящая в скобках,

где c_v - удельная теплоемкость (24.3.2) при постоянном объеме (24.3.3.1);

ρ = m / V - плотность газа.

Действительно,

Окончательно выражение для коэффициента теплопроводности χ будет иметь следующий вид:

Коэффициент 1/3 в этом выражении не заслуживает большого доверия ввиду грубости нашей модели, но зависимость χ от параметров, имеющих существенное значение, получилась верная.

25.5. Вязкость или внутреннее трение

Вязкость - это свойство жидкостей и газов оказывать сопротивление перемещению одной их части относительно другой.

Вязкость жидкостей и газов связана с переносом импульса упорядоченного движения p = m₀u между слоями жидкости (или газа), движущимися с различными скоростями u. Обмен молекулами и перенос их импульса происходит за счет теплового движения молекул и приводит к возникновению сил внутреннего трения.

25.5.1. Касательное (тангенциальное) напряжение сил внутреннего трения

Рассмотрим два слоя жидкости или газа, движущихся со скоростями u₁ и u₂, причем u₂ > u₁ (см. рисунок).

В результате обмена молекулами между слоями площадью dS возникают силы dF, действующие вдоль этих слоев. Сила dF, действующая на верхний слой, тормозит его. Равная по величине и противоположная по направлению сила dF' ускоряет нижний слой жидкости.

Величина силы dF, отнесенная к площади dS, называется касательным или тангенциальным напряжением τ.

25.5.2. Закон Ньютона для касательного напряжения сил внутреннего трения

Величина касательного напряжения τ определяется опытным законом Ньютона для сил внутреннего трения:

здесь η - коэффициент вязкости, его размерность ;

du/dz - градиент скорости упорядоченного движения среды.

25.5.3. Вязкость газов

Пусть скорость упорядоченного движения газа u зависит от одной координаты z, т.е. u = u(z) ≠ const.

Изобразим площадку dS, расположенную перпендикулярно оси z, и найдем импульс упорядоченного движения газа, переносимый молекулами за время dt через эту площадку.

Число молекул, пересекающих площадку dS за время dt, равно как и в (25.4.3):

Импульс упорядоченного движения одной молекулы, пересекающей площадку снизу:

Для каждой из молекул, пересекающих площадки dS сверху:

Полный импульс, перенесенный через площадку dS за время dt:

Силу dF получим из второго закона Ньютона (4.6), поделив dp на dt:

Поделив на dS, получим τ - касательное напряжение сил внутреннего трения:

Подставим сюда p₀₁, p₀₂ и dN, тогда

Приращение скорости упорядоченного движения на расстоянии 2λ заменим на дифференциал:

заметим, что nm₀=ρ - плотность газа.

С учетом этого имеем окончательно

25.5.4. Коэффициент вязкости газов

Сравнивая полученное выражение для касательного напряжения τ сил внутреннего трения с законом Ньютона для касательного напряжения (25.5.2), получим для коэффициента вязкости η следующее выражение:

Как и в случаях с коэффициентами диффузии D (25.3.4), теплопроводности χ (25.4.4) численный коэффициент 1/3 не вполне достоверен, но зависимость коэффициента вязкости от параметров газа наша формула дает верно.

25.6. Электропроводность (перенос заряда)

Связь плотности тока (10.2) с напряженностью электрического поля (9.3.3) дается, как известно (10.5), законом Ома в дифференциальной форме:

здесь σ - удельная проводимость проводника.

При наличии электрического поля в проводнике для электрических зарядов возникает неравновесная ситуация, в результате чего происходит перенос электрического заряда - течет электрический ток.

25.6.1. Вывод закона Ома в классической теории электропроводности

Плотность тока связана со средней скоростью упорядоченного движения зарядов , как мы знаем из (10.2.1), следующим соотношением:

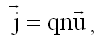
здесь q - заряд одного носителя заряда в проводнике;

n - концентрация носителей.

Для вывода закона Ома в дифференциальной форме нам надо установить связь между и .

В металле носителями заряда являются валентные электроны атомов металла, для них q = -e.

Следом за П. Друде будем считать, что валентные электроны в металле ведут себя подобно молекулам идеального газа. В такой модели электрон будет ускоряться электрическим полем в течении времени свободного пробега τ (25.2, 25.2.1). затем, как считал П. Друде, электрон ударяется об ион кристаллической решетки и полностью теряет скорость упорядоченного движения. После этого процесс повторяется.

Для равноускоренного движения при нулевой начальной скорости имеем следующий график зависимости u(t):

Максимальная скорость u_max будет достигнута при t = τ, т.е.:

При равноускоренном движении средняя скорость равна половине максимальной:

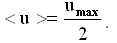
Для ускорения a из (4.6) и (9.3.3) имеем:

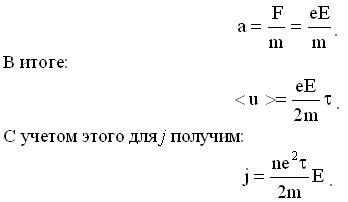
Сравнивая с формулой закона Ома: , видим, что коэффициент при E и есть σ - удельная проводимость проводника. Следовательно:

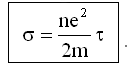
В металлах скорость упорядоченного движения электронов много меньше скорости теплового движения. Так из (23.4.2.5) при Т = 300К для электронов ( m = 9,1 · 10^-31 кг) получим:

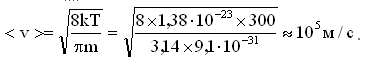
Для u при предельной плотности тока (в медных проводниках j_max = 10⁷ А/м²) при n = 10²⁹ м^-3 имеем:

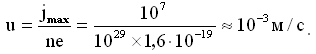
Следовательно, на время свободного пробега τ упорядоченное движение не влияет и можно считать, что:

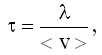
здесь λ - средняя длина свободного пробега электрона, которая определяется столкновениями свободных электронов с ионами металла.

Окончательно для удельной проводимости σ имеем:

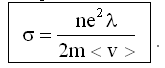
Так как (23.4.2.5), то из изложенной теории следует, что:

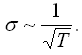
Между тем, опыт показывает, что для металлов:

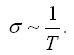
Это противоречие теории эксперименту можно устранить только на основе квантово-механического рассмотрения движения электрона в металле. Основы квантовой физики будут изложены во второй половине настоящего пособия, результаты квантовой теории электропроводности будут разобраны
в (29.4).