Физика в конспективном изложении. Часть III.

	ФИЗИКА в конспективном изложении. Часть 3

Содержание	Назад	Далее

КВАНТОВАЯ МЕХАНИКА

26. Открытие постоянной Планка

26.2.1.2. Спектральная плотность энергетической светимости r_λ

Спектральная плотность энергетической светимости - это отношение энергетической светимости dR, взятой в бесконечно малом интервале длин волн dλ, к величине dλ:

Спектральная плотность энергетической светимости r_λ является функцией длины волны λ и температуры Т.

Другое название r_λ- испускательная способность.

26.2.1.3. Связь R с r_λ

Из (26.2.1.2) получим, что

26.2.1.4. Спектральная плотность энергетической светимости r_ω

Спектральная плотность энергетической светимости r_ω - это отношение энергетической светимости dR, взятой в бесконечно малом интервале частот dω, к величине dω, т.е.:

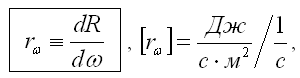
r_ω является функцией частоты ω и температуры Т. Величину r_ω называют, также как и r_λ , испускательной способностью тела.

Величину r_ω чаще используют в теоретических исследованиях, а r_λ - в экспериментальных.

26.2.1.5. Связь R с r_ω

Из (26.2.1.4) получим, что:

26.2.1.6. Связь r_λ и r_ω

Величины λ и ω, как мы знаем (15.1.8), связаны соотношением λ = 2πc / ω(для электромагнитной волны в вакууме v = c). Связь dλ и dω получим дифференцированием этого равенства:

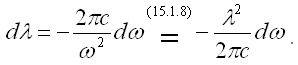
Знак минус указывает на то, что с ростом длины волны λ, круговая частота ω убывает.

Для соответствующих интервалов dλ и dω можно записать:

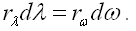
Заменив dλ на его выражения через dω и опуская знак минус, получим:

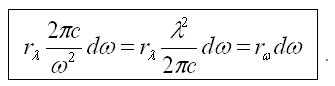
Используя эти выражения можно перейти от r_λ к r_ω и обратно.

26.2.1.7. Поток излучения Ф

Поток излучения Ф - это отношение энергии Е, переносимой электромагнитным излучением через какую-либо поверхность ко времени переноса, значительно превышающему период электромагнитных колебаний. Поток излучения Ф - синоним понятия мощность излучения. Единица измерения потока - ватт.

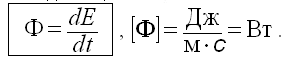
26.2.1.8. Поглощательная способность тела a_w

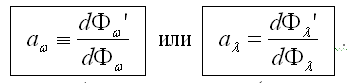
Поглощательная способность тела a_ω - это отношение поглощаемого телом потока излучения dФ_ω' (или dФ_λ') в интервале частот dω (или длин волн dλ) к падающему на него потоку dФ_ω (или dФ_λ) в том же интервале dω (или dλ), т.е.:

Поглощательная способность тела a_ω (как и a_λ) - величины безразмерные (это следует из определения).

26.2.1.9. Абсолютно черное тело

Абсолютно черное тело - это тело, для которого поглощательная способность тождественно равна единице для всех частот или длин волн и для любой температуры, т.е.:

Из определения абсолютно черного тела следует, что оно должно поглощать все падающее на него излучение.

Понятие "абсолютно черное тело" - это модельное понятие (1.3). В природе абсолютно черных тел не существует, но можно создать устройство, являющееся хорошим приближением к абсолютно черному телу - модель абсолютно черного тела.

26.2.1.10. Модель абсолютно черного тела

Модель абсолютно черного тела - это замкнутая полость с маленьким, по сравнению с ее размерами, отверстием. Полость изготавливают из материала, достаточно хорошо поглощающего излучение. Излучение, попавшее в отверстие, прежде чем выйти из отверстия, многократно отражается от внутренней поверхности полости.

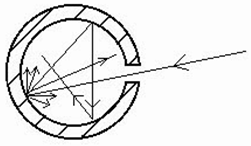
При каждом отражении часть энергии поглощается, в результате из отверстия выходит отраженный поток dФ'', являющийся очень малой частью попавшего в него потока излучения dФ. В результате поглощательная способность отверстия в полости будет близка к единице.

Если внутренние стенки полости поддерживать при температуре Т, то из отверстия будет выходить излучение, свойства которого будут очень близки к свойствам излучения абсолютно черного тела. Внутри полости это излучение будет находиться в термодинамическом равновесии с веществом полости.

26.2.1.11. Спектральное распределение объемной плотности энергии излучения абсолютно черного тела

По определению плотности энергии (9.12.1), объемная плотность энергии w(Т) равновесного излучения в полости - это:

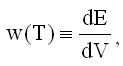
где dЕ - энергия излучения в объеме dV. Спектральное распределение объемной плотности дается функциями u(λ,T) (или u(ω,T)), которые вводятся аналогично спектральной плотности энергетической светимости (24.2.1.2 и 24.2.1.4), т.е.

Здесь dw_λ и dw_ω - объемная плотность энергии в соответствующем интервале длин волн dλ или частот dω.

26.2.2. Закон Кирхгофа

Закон Кирхгофа утверждает, что отношение испускательной способности тела (26.2.1.2, 26.2.1.4) к его поглощательной способности (26.2.1.8) одинаково для всех тел и является универсальной функцией частоты ω (или длины волны λ) и температуры Т, т.е.:

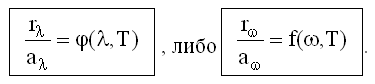
Очевидно, что поглощательная способность a_ω (или a_λ) для разных тел разная, то из закона Кирхгофа следует, что чем сильнее тело поглощает излучение, тем сильнее оно должно это излучение испускать. Так как для абсолютного черного тела a_ω ≡ 1 (или a_λ ≡ 1) (26.2.1.9), то отсюда следует, что в случае абсолютно черного тела f(ω,T) = r_ω и φ(,T) = r_λ.

Иными словами, f(ω,T) либо φ(λ,T), есть не что иное как, спектральная плотность энергетической светимости (или испускательная способность) абсолютно черного тела.

Функция φ(λ,Т) и f(ω,Т) связаны со спектральной плотностью энергии излучения абсолютно черного тела следующими соотношениями:

где c - скорость света в вакууме.

26.2.2.1. Как найти на опыте спектральную плотность энергетической светимости абсолютного черного тела

Схема установки для опытного определения зависимости φ(λ,Т) приведена на следующем рисунке.

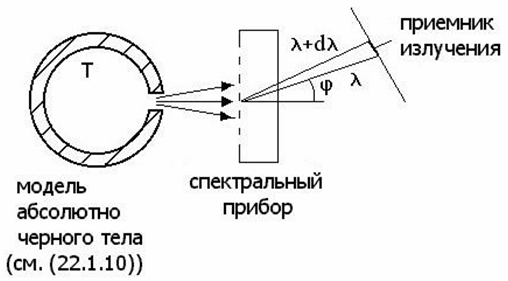
Излучение испускается из отверстия замкнутой полости, нагретой до температуры Т, затем попадает на спектральный прибор (призменный или решеточный монохроматор), который выделяет излучение в интервале частот от λ до λ + dλ. Это излучение попадает на приемник, который позволяет измерить падающую на него мощность излучения. Поделив эту приходящуюся на интервал от λ до λ + dλ мощность на площадь излучателя (площадь отверстия в полости!), мы получим значение функции φ(λ,Т) для данной длины волны λ и температуры Т. Полученные экспериментальные результаты воспроизведены на следующем рисунке.

26.2.3. В чем состояла проблема излучения абсолютно черного тела?

Проблема состояла в том, чтобы теоретически получить зависимость φ(λ,Т) - спектральную плотность энергетической светимости абсолютно черного тела.

Казалось, что ситуация ясна: при заданной температуре Т молекулы вещества излучающей полости (26.2.1.10) имеют максвелловское распределение по скоростям (23.4) и излучают электромагнитные волны в соответствии с законами классической электродинамики (16). Излучение находится в термодинамическом равновесии с веществом (26.2.1), значит для нахождения спектральной плотности энергии излучения u(λ,T) и связанной с ней функции φ(λ,Т) можно использовать законы термодинамики (24) и классической статистики (23).

Однако, все попытки теоретиков получить на основе классической физики закон излучения абсолютно черного тела потерпели неудачу.

Частичный вклад в решение этой проблемы внесли Густав Кирхгоф, Вильгельм Вин, Иозеф Стефан, Людвиг Больцман, Джон Уильям Релей, Джеймс Хонвуд Джинс.

26.2.4. Формула Планка

Проблема излучения абсолютно черного тела была решена Максом Планком. Для этого ему пришлось отказаться от классических представлений и сделать предположение о том, что заряд, совершающий колебания с частотой ν, может получать или отдавать энергию порциями, или квантами.

Величина кванта энергии (26.1.3):

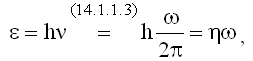
где h - постоянная Планка (26.1.2);

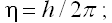
η - частота колебаний электромагнитной волны, излученной колеблющемся зарядом;

ω = 2πν - круговая частота.

26.2.4.1. Формула Планка для u(ω, T) - функции распределения плотности энергии в спектре излучения абсолютно черного тела

На основе представления о квантах энергии М. Планк, используя методы статистической термодинамики (22.1.8), получил выражение для функции u(ω,Т), дающей распределение плотности энергии в спектре излучения абсолютного черного тела:

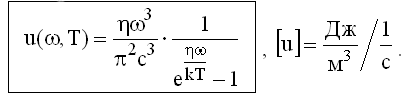
Вывод этой формулы будет дан в (29.6.3).

26.2.4.2. Формула Планка для f(ω,T) - спектральной плотности энергетической светимости в зависимости от циклической частоты w

Помножив u(ω,T) на dw получим u(ω,T)dω - плотность энергии в интервале частот dω, помножив которую на скорость распространения электромагнитной волны "с" получим f(ω,T)dω ≡ dj_ω - плотность потока энергии в интервале частот от ω до ω + dω (в предположении, что все излучение распространяется в одном направлении: dj_ω = cu(ω,T)dω). Учет различных направлений излучения дает численный коэффициент ¼, в результате чего:

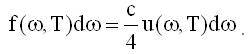
Отсюда получим связь f(ω,T) - спектральной плотности энергетической светимости, с u(ω,T) - спектральным распределением равновесной плотности энергии излучения абсолютно черного тела:

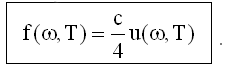
Используя это соотношение и формулу Планка (22.2.4.1) для u(ω,T), получим, что:

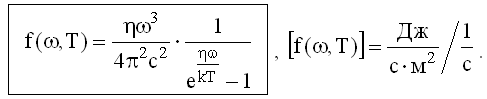
Это и есть формула Планка для спектральной плотности энергетической светимости f(ω,T).

26.2.4.3. Формула Планка для φ(λ,Т)

Как мы знаем из (26.2.2), в случае абсолютно черного тела f(ω,T)=r_λ, а φ(λ,Т)=r_ω.

Связь между r_λ и r_ω была получена в (26.2.1.6), значит:

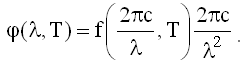
Здесь мы аргумент ω функции f(ω,Т) выразили через длину волны λ. Подставляя сюда формулу Планка для f(ω,Т) из (26.2.4.2), получим формулу Планка для φ(λ,Т) - спектральной плотности энергетической светимости в зависимости от длины волны λ:

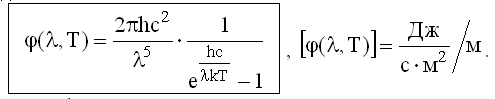
График этой функции хорошо совпадает с экспериментальными графиками φ(λ,Т) для всех длин волн и температур.

Это и означает, что проблема излучения абсолютно черного тела решена.

26.2.4.4. Закон Стефана-Больцмана для энергетической светимости R(Т).

Из (26.2.1.5) для абсолютно черного тела, когда r_ω = f(λ,T), получим энергетическую светимость R(T), интегрируя функцию f(ω,T) во всем интервале частот.

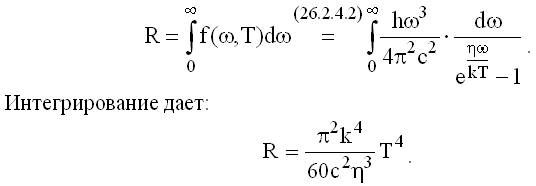
Введем обозначение:

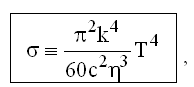
тогда выражение для энергетической светимости R примет следующий вид: R = σT^4.

Это и есть закон Стефана-Больцмана.

М. Стефан на основе анализа опытных данных пришел в 1879 г. к выводу, что энергетическая светимость любого тела пропорциональна четвертой степени температуры.

Л. Больцман в 1884 г. нашел из термодинамических соображений, что такая зависимость энергетической светимости от температуры справедлива лишь для абсолютно черного тела.

Постоянная σ носит название постоянной Стефана-Больцмана. Ее экспериментальное значение:

Вычисления по теоретической формуле дают для σ результат очень хорошо согласующийся с экспериментальным.

Отметим, что графически энергетическая светимость равна площади, ограниченной графиком функции f(ω,Т), это иллюстрирует предыдущий рисунок.

26.2.4.5. Закон смещения Вина

Максимум графика спектральной плотности энергетической светимости φ(λ,Т) при повышении температуры смещается в область более коротких волн. Для нахождения закона, по которому происходит смещение максимума φ(λ,Т) в зависимости от температуры, надо исследовать функцию φ(λ,Т) на максимум. Определив положение этого максимума, мы получим закон его перемещения с изменением температуры.

Как известно из математики, для исследования функции на максимум надо найти ее производную и приравнять к нулю:

Подставив сюда φ(λ,Т) из (26.2.4.2) и взяв производную, получим три корня алгебраического уравнения относительно переменной λ. Два из них (λ = 0 и λ = ∞) соответствуют нулевым минимумам функции φ(λ,Т). Для третьего корня получается выражение:

Введем обозначение:

тогда положение максимума функции φ(λ,Т) будет определятся простой формулой:

Это и есть закон смещения Вина.

Он назван так в честь В. Вина, теоретически получившим в 1894 г. это соотношение. Постоянная в законе смещения Вина имеет следующее численное значение:

26.3. Проблема фотоэффекта

26.3.1. Что такое фотоэффект

Фотоэффект - это испускание электронов веществом под действием электромагнитных волн.

Такой фотоэффект называют внешним. Именно о нем мы будем говорить в этой главе. Есть еще и внутренний фотоэффект. О нем - позже (30.2.5).

26.3.2. Немного из истории фотоэффекта

В 1887 г. немецкий физик Генрих Герц обнаружил, что ультрафиолетовый свет, освещающий отрицательный электрод в разряднике, облегчает прохождение разряда. В 1988-89 гг. русский физик А. Г. Столетов занимается систематическим исследованием фотоэффекта (схема его установки приведена на рисунке). Исследования проводились в атмосфере газа, что сильно усложняло происходившие процессы.

Столетов обнаружил, что:

1)     наибольшее воздействие оказывают ультрафиолетовые лучи;

2)     сила тока возрастает с увеличением интенсивности света, освещающего фотокатод;

3)     испущенные под действием света заряды имеют отрицательный знак.

Дальнейшие исследования фотоэффекта производились в 1900-1904 гг. немецким физиком Ф. Ленардом в наивысшем достигнутом в то время вакууме.

Ленарду удалось установить, что скорость вылетающих из фотокатода электронов не зависит от интенсивности света и прямо пропорционально его частоте. Так родилась проблема фотоэффекта. Объяснить результаты опытов Ленарда на основе электродинамики Максвелла было невозможно!