ФИЗИКА в конспективном изложении. Часть 3

Содержание Назад Далее

 

КВАНТОВАЯ МЕХАНИКА

26.3.3. Опытное исследование фотоэффекта

23.3.3.1. Описание экспериментальной установки

На рисунке изображена установка, позволяющая детально изучать фотоэффект.

Электроды, фотокатод и анод, помещены в баллон, из которого откачан воздух. Свет на фотокатод подается через кварцевое окошко. Кварц, в отличие от стекла, хорошо пропускает ультрафиолетовые лучи. Разность потенциалов (напряжение) между фотокатодом и анодом измеряет вольтметр. Ток в цепи анода измеряется чувствительным микроамперметром. Для регулировки напряжения батарея питания подключена к реостату со средней точкой. Если движок реостата стоит против средней точки, подсоединенной через микроамперметр к аноду, то разность потенциалов между фотокатодом и анодом равна нулю. При смещении движка влево, потенциал анода становится отрицательным относительно катода. Если движок реостата сдвигать вправо от средней точки, то потенциал анода становится положительным.

26.3.3.2. Вольт-амперная характеристика установки по изучению фотоэффекта. Следствия из нее

Вольт-амперная характеристика - это зависимость фототока i от напряжения между катодом и анодом U. При освещении светом, частота n которого достаточна для возникновения фотоэффекта, вольт-амперная характеристика имеет следующий вид:

Из этой характеристики следует, что при некотором положительном напряжении на аноде фототок i достигает насыщения. При этом все электроны, испущенные фотокатодом в единицу времени, попадают за это же время на анод.

При U = 0 часть электронов долетает до анода и создает фототок i₀. При некотором отрицательном напряжении на аноде - U_зад - фототок прекращается. При этом значении напряжения максимальная кинетическая энергия фотоэлектрона у фотокатода (mV²_max)/2 полностью расходуется на совершение работы против сил электрического поля (9.6.2):

В этой формуле m_e - масса электрона; v_max - его максимальная скорость у фотокатода; e - абсолютное значение заряда электрона.

Таким образом, измерив задерживающее напряжение U_зад, можно найти кинетическую энергию (и скорость электрона) сразу после его вылета из фотокатода.

Опыт показал, что

1)    энергия вылетевших из фотокатода электронов (и их скорость) не зависела от интенсивности света! При изменении частоты света ν меняется и U_зад, т.е. максимальная кинетическая энергия электронов, покидающих фотокатод;

2)    максимальная кинетическая энергия электронов, у фотокатода, (mv²_max)/2, прямо пропорциональна частоте ν света, освещающего фотокатод.

26.3.3.3. В чем состояла проблема фотоэффекта?

Проблема, как и в случае с излучением абсолютно черного тела, состояла в том, что теоретические предсказания, сделанные для фотоэффекта на основе классической физики (электродинамики Максвелла), противоречили результатам опытов. Интенсивность света I в классической электродинамике является плотностью потока энергии световой волны (16.5.4). Во-первых, с этой точки зрения, энергия, передаваемая световой волной электрону, должна быть пропорциональна интенсивности света. Опыт (26.3.3.2) не подтверждает это предсказание. Во-вторых, в классической электродинамике нет никаких объяснений прямой пропорциональности кинетической энергии электронов, (mv²_max)/2, частоте света ν.

26.3.4. Уравнение Эйнштейна для фотоэффекта

Согласно предположению Эйнштейна свет состоит из неделимых квантов энергии величиной hν. Это предположение позволило ему очень просто разрешить проблему фотоэффекта. Применим к фотоэффекту закон сохранения энергии, считая свет потоком фотонов с энергией

В металле электрон находится в потенциальной яме. Для того, чтобы удалить электрон из металла, надо совершить работу против сил электростатического притяжения отрицательного электрона к положительному ионному остатку. Эта работа А называется работой выхода электрона из металла. Будем пока считать, что глубина потенциальной ямы равна этой работе А, впоследствии (29.5) мы внесем некоторые уточнения. Для разных металлов величина А разная. Меньше всего величина работы выхода у щелочных металлов, например, для цезия (Cs) А = 1,81 эВ. У цинка, который использовался в опытах Столетова, А = 4,24 эВ. Фотоны поглощаются поодиночке (если интенсивность света не достигает очень больших значений). Энергия фотона hν частично расходуется на работу выхода, оставшаяся часть (mv²_max)/2 уносится электроном, (см. предыдущий рисунок).

Таким образом

Это и есть уравнение Эйнштейна для фотоэффекта. Если в этом уравнении заменить (mv²_max)/2 на  еU_зад  (см. (26.3.3.2)), то уравнение Эйнштейна будет иметь следующий вид:

Из последней формулы видно, что величина задерживающего напряжения U_зад прямо пропорциональна частоте света. Эту зависимость тщательно проверял в специально созданной установке американский физик Р. Милликен. "Я потратил десять лет моей жизни на проверку этого эйнштейновского уравнения 1905 г., - писал Милликен, - и вопреки всем моим ожиданиям я вынужден был в 1915 г. безоговорочно признать, что оно экспериментально подтверждено, несмотря на его несуразность, так как казалось, что оно противоречит всему, что мы знаем об интерференции света.". Последняя часть высказывания Р. Милликена связана с корпускулярно-волновым дуализмом микрочастиц, о котором мы поговорим позднее (27).

26.3.4.1. Красная граница фотоэффекта

Из уравнения Эйнштейна для фотоэффекта (26.3.4) следует, что если энергия фотона hν меньше работы выхода А, то фотоэффект невозможен. Граничная частота определяется равенством:

здесь ν_кр - красная граница фотоэффекта.

Соответствующая частоте ν_кр длина волны также называется красной границей фотоэффекта, т.к. ν = c/λ (15.1.8), то для λ_кр имеем:

Название "красная граница" связано с тем, что длинноволновая часть видимого спектра, для которой максимальна длина волны λ и минимальна энергия фотонов, имеет красный цвет.

26.4. Боровская теория атома водорода

Атом водорода - простейший из всех атомов. Его ядро - элементарная частица протон. Масса протона в 1836 раз больше массы электрона, вследствие этого ядро можно считать неподвижным и рассматривать только движение электрона.

Заряд протона равен e, он положительный и равен по абсолютной величине заряду электрона, поэтому между ядром и электроном действует кулоновская сила притяжения (9.2.2).

здесь e = 1,6·10^-19 Кл - элементарный заряд.

По второму закону Ньютона (4.6):

При равномерном движении по окружности радиуса r нормальное ускорение электрона (3.10.1):

После подстановки этого выражения во второй закон Ньютона получим уравнение движения электрона:

Из этого уравнения не следует никаких ограничений на r - радиус орбиты электрона. Применим условие стационарности состояния атома (26.1.6):

С помощью этого условия исключим из уравнения скорость v.
В результате для радиусов стационарных орбит r_n получим:

Радиус первой орбиты (n = 1). называется первым боровским радиусом, его обозначают r₀. Численное значение первого боровского радиуса:

Полная энергия E атома водорода в нашей модели равна сумме кинетической энергии (m_ev²_max)/2 и отрицательной потенциальной энергии взаимодействия электрона с ядром: (-e²)/(4πε₀r), т.е.

Из уравнения движения электрона заменим mv²/2 на e²/(8πε₀r), тогда полная энергия атома водорода

Подставив сюда выражение для r_n, получим E_n - энергию стационарного состояния атома водорода, зависящую от главного квантового числа n:

Состояние атома водорода при главном квантовом числе n = 1 называется основным состоянием. Численное значение энергии основного состояния атома водорода

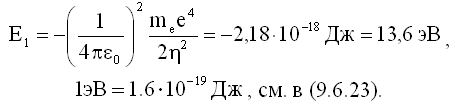
С учетом значения E₁ энергия стационарного состояния  имеет простой вид:

26.4.1. Спектр излучения атома водорода в теории Бора

Изобразим в масштабе энергетические уровни атома водорода E_n в зависимости от главного квантового числа n.

Согласно второму постулату Бора (26.1.6) энергия излученного фотона, νω, равна разности энергий стационарных состояний, между которыми происходит квантовый переход:

 , в случае излучения n > m.

Подставляя сюда выражения для E_n и E_m, (24.4) для частоты ν, получим:

здесь  - постоянная Ридберга, она так названа в честь шведского физика И. Ридберга.

Так как λ = c/ν, то для длины волны λ получим следующее выражение:

Здесь R'= R/c = 1,097·10⁷ 1/м - тоже называют постоянной Ридберга.

26.4.1.1. Спектральные серии атома водорода

Из теории Бора следует, что спектр атома водорода имеет линейчатый характер, причем, наблюдаемые линии объединены в спектральные серии. Задается серия номером m уровня, на который происходит квантовый переход. Первые серии названы именами ученых-физиков:

Спектры атома водорода были изучены экспериментально до создания Бором своей теории. Хорошее совпадение экспериментальных данных с выводами теории Бора для спектров атома водорода говорит в пользу этой теории.

Однако, попытки применить теорию Бора к более сложным атомам потерпели неудачу. В настоящее время теория атома Бора представляет исторический интерес как промежуточный этап к созданию более верной теории. Такая теория теперь существует - это квантовая механика.

Сибирская государственная геодезическая академия (СГГА), 2006.