Физика в конспективном изложении. Часть III.

	ФИЗИКА в конспективном изложении. Часть 3

Содержание	Назад	Далее

КВАНТОВАЯ МЕХАНИКА

27. Корпускулярно-волновой дуализм микрообъектов

Корпускулярно-волновой дуализм заключается в том, что всем микрообъектам (фотонам, электронам, протонам, нейтронам и т.д.) присущи одновременно и корпускулярные и волновые свойства. В одних условиях микрообъекты проявляют себя как частицы, обладающие определенной энергией Е и импульсом а в других обнаруживают свою волновую природу (в явлениях интерференции и дифракции.)

Впервые корпускулярно-волновой дуализм был установлен для света. Затем (1923 г.) французский физик Л. де Бройль высказал гипотезу о всеобщем характере корпускулярно-волнового дуализма (27.2).

27.1. Свойства фотонов

Фотон - это элементарная частица, квант электромагнитного излучения.

27.1.1. Скорость, масса, энергия и импульс фотона

1.     Скорость фотона всегда постоянна и равна скорости света в вакууме.

2.     Масса фотона

3.     Энергия фотона

4.     Импульс фотона , здесь k = ω/c - волновое число; - волновой вектор (15.2.4.1).

Выражения для импульса фотона следует из релятивистского инварианта (8.7.3.3) с учетом того, что масса фотона m_γ = 0. В самом деле, из (8.7.3.3):

27.1.2. Неделимость фотона

Это свойство фотона означает, что фотон частоты ω всегда регистрируется как частица, несущая энергию ε = νω. Нельзя получить фотоны той же самой частоты w, но с энергией e' = e/2! Рассмотрим мысленный опыт с полупрозрачным зеркалом, разделяющим пучок света интенсивностью I на две части, интенсивностью I/2 каждая. Схема этого мысленного опыта изображена на следующем рисунке.

Предположим, что сначала интенсивность света I велика. Тогда по величине фототока i фотоэлементов 1 и 2 можно судить об интенсивностях пучков I₁ и I₂ (26.3.2). Такой опыт можно проделать реально и убедиться в том, что наше полупрозрачное зеркало действительно делит интенсивный пучок пополам. Разумеется надо подобрать фотоэлемент с работой выхода A < ηω, это условие необходимо для наблюдения фотоэффекта (26.3.4.1).

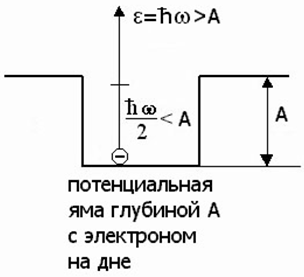
Теперь изменим условие опыта. Пусть интенсивность пучка, идущего от источника света, так мала, что фотоны проходят через нашу установку поодиночке. Пусть соотношение между работой выхода и энергией фотона удовлетворяет еще одному условию: Вместе с предыдущим условием мы имеем:

Как видно на изображенной энергетической схеме фотоэффекта, целый фотон с энергией e вызовет фотоэффект и фотоэлемент сработает ( A < ηω ), половина же фотона не сможет заставить сработать фотоэлемент (). Логически при прохождении одиночных фотонов возможны два варианта.

Первый вариант: каждый фотон делится пополам, так что после полупрозрачного зеркала энергия разделенных фотонов ε' = ε/2. Тогда фотоэлементы 1 и 2 перестают срабатывать. Но, если в этом случае убрать полупрозрачное зеркало, то целые фотоны с энергией ε = ηω > A попадут на фотоэлемент 1 и он будет срабатывать.

Второй вариант: фотон не делится зеркалом пополам, а либо целиком попадает на фотоэлемент 1, либо, целиком же, попадает на фотоэлемент 2, заставляя их срабатывать попеременно.

Реальные опыты с фотонами показывают, что в действительности осуществляется второй вариант: фотон неделим!

27.1.3. Интерференция одиночных фотонов

Дополним нашу установку по "расщеплению" фотонов (27.1.3) еще одним элементом: зеркалом, отражающим второй пучок так, чтобы он встретился с первым. В месте встречи поставим экран наблюдения, вдоль которого расположим достаточно маленькие фотоэлементы, но их размер Δх должен быть больше, чем длина волны света λ.

При большой интенсивности пучка I мы получим на экране наблюдения интерференционную картину от двух источников (18.1.2.4) с чередованием максимумов и минимумов интенсивности. Ее можно наблюдать непосредственно, а можно зафиксировать с помощью нашей системы фотоэлементов, скажем, в памяти компьютера.

Что произойдет, если интенсивность пучка опять сделать такой же малой, как и во второй части опыта по "расщеплению" фотонов (27.1.2), так, чтобы фотоны проходили нашу установку поодиночке?

Получим мы в этом случае интерференционную картину или нет?

Как мы знаем (18), интерференционная картина возникает от наложения двух (или больше) когерентных волн света (электромагнитных волн). Если фотон совершенно неделим (27.1.2), то при прохождении одиночных фотонов накладываться друг на друга нечему. И в этом случае интерференционная картина не должна сформироваться, сколько бы времени мы не накапливали информацию о срабатывании наших фотоэлементов в памяти компьютера (вспомните заключительную часть высказывания Милликена (26.3.4)).

Но опыт показывает, что с течением времени на экране наблюдения формируется интерференционная картина с тем же самым расположением максимумов и минимумов, как и при большой интенсивности света.

Что же делится в нашей установке пополам и накладывается друг на друга? Делится электромагнитная волна, связанная с фотоном! В зависимости от разности хода две волны усиливают или ослабляют друг друга (18.2.4). Фотоны, как показывает опыт, чаще попадают в те места, где интенсивность волны больше. Это и приведет с течением времени к формированию одиночными фотонами интерференционной картины.

27.1.4. Вероятностная интерпретация плотности энергии и интенсивности электромагнитной волны

Результаты мысленных экспериментов, рассмотренных в (27.1.3) и (27.1.4), позволяют сформулировать некоторые выводы.

1. Распространение фотонов в пространстве в некотором смысле правильно описывается уравнениями Максвелла (16) для электромагнитной волны. Электромагнитная волна, падающая на полупрозрачное зеркало, действительно "расщепляется" на две волны, которые могут интерферировать друг с другом.

2. Величины (16.3) и I ~ E² (16.5.4) в случае малой интенсивности волны (малых значений напряженности электрического поля E и индукции магнитного поля B = μ₀H) не могут быть истолкованы как плотность энергии и плотность потока энергии (интенсивность света). Величина w (также как и I) может быть сделана сколь угодно малой, а энергия, передаваемая фотоном фотоэлементу, всегда конечна и равна ην!

3. Правильная интерпретация величин, пропорциональных E² и Н², состоит в том, что они определяют вероятность обнаружения фотона в некоторой области пространства.

Таким образом энергию переносит фотон, а электромагнитная волна дает только вероятность обнаружения этого фотона. Плотность энергии w одиночного фотона равна произведению энергии фотона на вероятность его нахождения в данной области пространства.

При очень большом числе фотонов (больших интенсивностях света) величина w дает среднюю плотность энергии, создаваемую этими фотонами (см. также (16.5.1)).

27.2. Гипотеза де Бройля. Волновые свойства электронов

Согласно гипотезе де Бройля любой движущийся частице с энергией E и импульсом соответствует волна с частотой ν = E/h, длиной волны λ = h/p и волновым вектором . Так же как в случае с фотоном, с соответствующей волной связаны частицы, обладающие энергией E = hν и импульсом

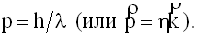
С фотонами связаны электромагнитные волны (16.1). Волны, для частиц с m ≠ 0, о существовании которых догадался Л. де Бройль, носят название волн де Бройля. Длина волны де Бройля:

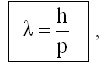
здесь p - импульс частицы.

Сопоставим свойства фотона и электрона, известные Л. де Бройлю во время публикации своих работ (1923-24 гг.)

27.2.1. Почему мы не наблюдаем волновых свойств у макроскопических тел?

Волновые свойства - это интерференция и дифракция. Для наблюдения интерференции и дифракции волн необходимо экспериментальное устройство, создающее разность хода Δ (18.1.23) порядка длины волны λ.

Найдем длину волны де Бройля для тела массой m = 1 г = 10^-3 кг и движущегося со скоростью v = 1 м/с.

Так как v << c, то импульс тела можно найти по классической формуле p = mv (4.5). Тогда:

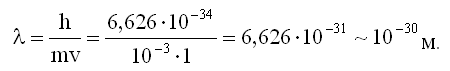
Мы видим, что длина волны де Бройля для макроскопических тел чрезвычайно мала. Для сравнения, размеры атомов и межатомных растояний в твердых телах порядка ангстрема, м (22.1.2). Следовательно, мы не сможем создать устройство, обеспечивающее разность хода Δ ~ 10^-30 м, эта величина меньше межатомных расстояний в 10²⁰=100 000 000 000 000 000 000 раз!

27.2.2. Оценка длины волны де Бройля для электрона

Пусть наш электрон ускоряется разностью потенциалов U = 100 в. При такой разности потенциалов можно пользоваться ньютоновскими формулами для энергии и импульса. Выразим кинетическую энергию через импульс электрона p=mv; mv²/2=p²/2m. Затем работу электрического поля eU (9.6.2) приравняем к полученной электроном кинетической энергии (5.5; 5.8):

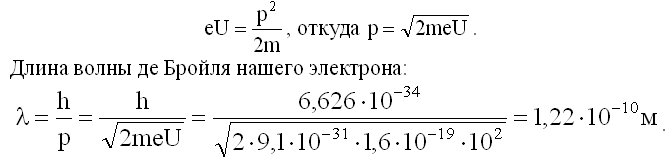
Полученная величина имеет порядок межатомных расстояний в кристалле, значит отражение "электронных волн" от поверхностных слоев атомов кристалла можно использовать для обнаружения волновых свойств электронов.

27.2.3. Опыт Дэвиссона и Джермера

Американские физики Дэвиссон и Джермер обнаружили в 1927 г. волновые свойства электронов в эксперименте по отражению электронов от поверхности монокристалла никеля.

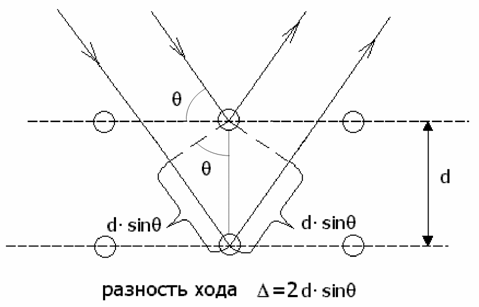
Волны де Бройля электронов частично отражались от поверхности монокристалла никеля, частично - от второго слоя атомов, тем самым между отраженными волнами создавалась известная разность хода Δ = 2d·sinΘ (см. рисунок). Условие максимума первого порядка интерференции двух волн имеет, как известно (18.1.2.3), следующий вид: Δ= λ.

При Δ = 2d·sinΘ получим условие максимума для волн, отраженных от двух поверхностных слоев кристалла .

Постоянная решетки кристалла никеля d была известна и для определенного угла Θ можно было рассчитать длину волны λ, при которой должен был наблюдаться максимум. Длину волны де Бройля электронов в опыте Дэвиссона и Джермера можно очень просто изменять, изменяя ускоряющую разность потенциалов U (27.2.2). Опыт показал, что максимум отраженного электронного пучка наблюдался при значениях длин волн де Бройля электронов очень близких к расчетным.

Позднее волновые свойства были обнаружены у нейтронов, атомных и молекулярных пучков. Во всех случаях эксперименты подтверждали связь между длиной волны де Бройля и импульсом частицы.

27.2.4. Опыт Бибермана, Сушкина, Фабриканта по интерференции одиночных электронов

В опытах Дэвиссона и Джермера интенсивность электронных пучков была велика. Возникает вопрос, появится ли дифракционная картина в случае, если электроны проходят через экспериментальную установку, например, кристалл, представляющий собой дифракционную решетку, поодиночке (аналогично одиночным фототонам в (27.1.3)). Опыт с одиночными электронами выполнили в 1949 г. советские физики Л. М. Биберман, Н. Г. Сушкин и В. А. Фабрикант. Они наблюдали дифракционную картину электронного пучка от мелкокристаллического тела. Разумеется, один электрон не даст сразу интерференционной картины, он будет просто зафиксирован целиком в определенном месте пространства. Но с течением времени, как показал опыт, формируется такая же дифракционная картина, как и при большой интенсивности пучка. Следовательно, волновые свойства нельзя объяснить взаимодействием различных электронов в интенсивном пучке, они присущи каждому одиночному электрону.

27.2.5. Мысленный эксперимент по дифракции электронов на двух щелях

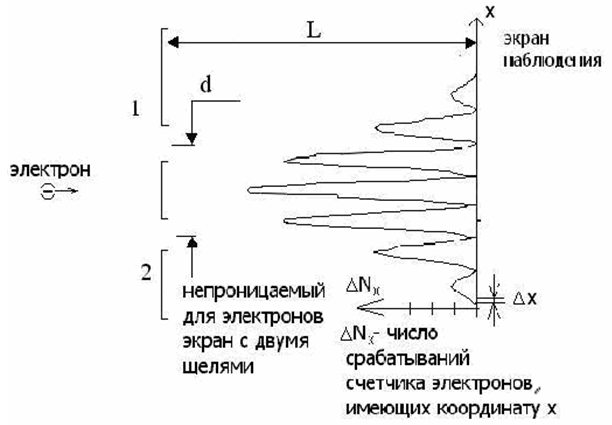
Мы рассмотрим идеализацию действительного опыта - мысленный эксперимент по дифракции электронов на двух щелях. Схема этого мысленного эксперимента такая же как и у опыта Юнга (18.2.1) по интерференции света.

Электронный пучок направляется на непрозрачный экран с двумя щелями, расположенными на расстоянии d друг от друга. Электроны фиксируются маленькими счетчиками, размером в Δx, расположенными вдоль экрана наблюдения.

При интенсивном пучке электронов графиком зависимости числа срабатываний счетчиков от координаты x будет интерференционная кривая: чередование максимумов и минимумов (точнее, ступенчатая функция - гистограмма, но при малых Δx ее ступенчатость будет мала).

Что будет происходить в этой установке, если электроны будут проходить ее поодиночке? Как показывает опыт (27.2.4) с течением времени сформируется точно такая же интерференционная картина как и с интенсивным пучком электронов. Как можно объяснить появление этой интерференционной картины? Электрон неделим, он всегда регистрируется целиком. Значит дебройлевская волна каждого электрона проходит одновременно через оба отверстия, затем волны, идущие от отверстий 1 и 2, интерферируют друг с другом. Электроны чаще попадают в те места экрана, где интенсивность результирующей волны больше. Здесь ситуация аналогична той, что была разобрана нами в случае интерференции одиночных фотонов (27.1.3).