ФИЗИКА в конспективном изложении. Часть 3

Содержание Назад Далее

 

КВАНТОВАЯ МЕХАНИКА

27. Корпускулярно-волновой дуализм микрообъектов

27.2.6. Волновая функция и волна де Бройля

Дальнейшее развитие физики показало, что волна де Бройля - частный случай более общего фундаментального понятия квантовой физики - волновой функции, которую обозначают греческой буквой Ψ.

В общем случае волновая функция - это комплексная функция координат и времени. Подробнее с волновой функцией мы познакомимся при изучении дифференциального уравнения - уравнения Шредингера (28), решением которого является волновая функция.

Волновая функция свободно движущейся частицы с точно заданным импульсом p и является волной де Бройля. В частном случае движения вдоль оси х она имеет вид плоской волны:

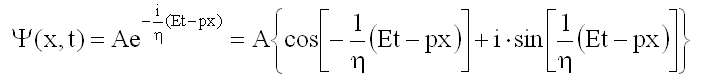
здесь А - нормировочная постоянная;

E - энергия частицы;

p - ее импульс;

e = 2,73.. - основание натуральных логарифмов;  - мнимая единица.

27.2.7. Вероятностный смысл волновой функции. Условие нормировки

В 1926 г. Макс Борн дал вероятностную интерпретацию волновой функции Ψ, согласно которой квадрат модуля волновой функции  определяет вероятность dw того, что микрообъект будет обнаружен в пределах объема dV, т.е.

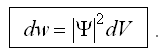
Здесь  - это комплексно-сопряженная функция, которая отличается от Ψ тем, что мнимую единицу i заменяют на -i. Напомним, что . Произведение i на (-i) дает единицу, в самом деле, , таким образом вероятность dw будет определяться, как и требуется, положительным числом.

На функцию Ψ накладывается условие нормировки, которое следует из того, что полная вероятность w обнаружить частицу в любом месте доступного ей пространства должна быть равна единице, т.е.:

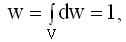
Подставляя сюда dw, получим условие нормировки для волновой функции Ψ:

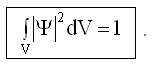
27.3. Соотношения неопределенностей

Математически соотношение неопределенностей имеет вид неравенства:

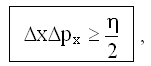
где Δх - неопределенность координаты микрочастицы;

Δp_x - неопределенность соответствующей компоненты импульса.

Для Δy Δp_y и ΔzΔp_z справедливы аналогичные соотношения.

Соотношения неопределенностей были установлены в 1927 г. немецким физиком Вернером Гейзенбергом.

27.3.1. Связь соотношения неопределенностей с корпускулярно-волновым дуализмом

Соотношения неопределенностей являются следствием корпускулярно-волнового дуализма квантовых объектов.

Задолго до создания квантовой механики в оптике было известно соотношение между длиной цуга световой волны Δx и неопределенностью волнового числа этого цуга Δk (19.4.4.4).

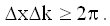
С учетом соотношения де Бройля (27.2)

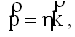
получим 

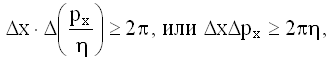
что по порядку величины совпадают со сформулированным выше соотношением неопределенностей.

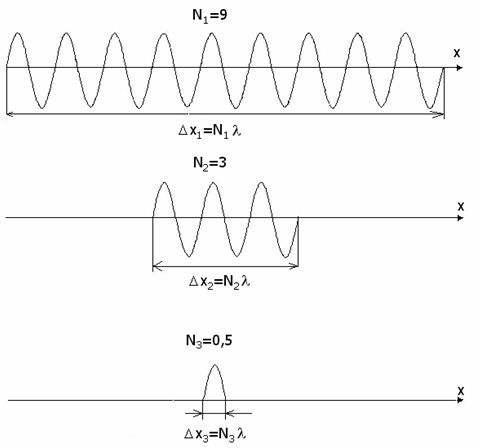
Для того, чтобы пояснить физический смысл соотношения неопределенностей, рассмотрим три различные волновые функции (27.2.6), изображенные на рисунках. (т.к. волновая функция является комплексной, то будем считать, что изображены вещественные части волновых функций). Наши волновые функции представляют собой цуги гармонических волн разной протяженности, распространяющиеся вдоль оси x.

В соответствии с вероятностным смыслом волновой функции (27.2.7) микрообъект можно обнаружить только там, где волновая функция отличается от нуля. Это значит, что неопределенность, с которой наши волновые функции задают координату х микрообъекта, совпадает с пространственной протяженностью соответствующих волновых функций. Из рисунка видно, что неопределенности координаты х для наших частиц удовлетворяют неравенствам: Δx₁ > Δx₂ > Δx₃.

Для неопределенностей импульса Δp_x - ситуация обратная. Так как p=h/λ (27.2), то ясно, что Δp_x связан с Δλ. Продифференцировав формулу, связывающую p с λ, получим:

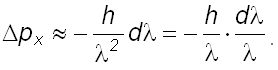
Заменяя дифференциалы приращениями, а h/λ через p_x (27.2) и опуская минус, получим:

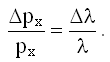
Т.е. относительная неопределенность импульса Δp_x/p_x равна относительной неопределенности длины волны Δλ/λ.

Величина Δλ/λ меньше всего для первой волновой функции, а самая большая - для третьей. Грубой мерой для Δλ/λ может служить величина 1/N, где N - число полных волн, из которых состоит цуг, т.е.:

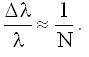
Учитывая связь с Δp_x/p_x, получим:

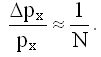
Из рисунков видно, что тогда:

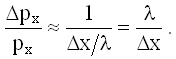
Наконец, заменив в этом выражении λ на h/p_x, получим после простых преобразований:

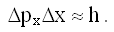
Мы рассматривали волновые функции, представляющие собой отрезки синусоид. Для волн любой формы полученное нами соотношение принимает форму неравенства:

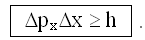
Отметим, что в приведенном в (27.3) соотношении неопределенностей , равенство достигается в случае, если волновые функции представляют из себя гауссовы волновые пакеты.

Лабораторная работа №73-к. Изучение корпускулярно-волнового дуализма микрочастиц.