ФИЗИКА в конспективном изложении. Часть 3

Содержание Назад Далее

 

КВАНТОВАЯ МЕХАНИКА

28. Уравнение Шредингера. Элементы квантовой механики

Волновое уравнение, позволяющее найти волновую функцию частицы, которая движется в заданном силовом поле, имеет следующий вид:

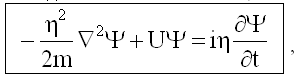
здесь η = 1,05·10^-34 Дж·с - постоянная Планка;

m - масса частицы;

U - ее потенциальная энергия во внешнем поле, которая, вообще говоря, может зависеть и от времени t,  - мнимая единица, через обозначен оператор Лапласа. Оператор - это совокупность действий, которые надо провести над функцией. В декартовой системе координат оператор Лапласа имеет вид:

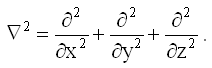
Волновое уравнение для функции Ψ получено в 1926 г. австрийским физиком Эрвином Шредингером и носит его имя - уравнение Шредингера.

В квантовой механике уравнение Шредингера играет такую же фундаментальную роль, как и уравнения движения Ньютона в классической механике.

28.1. Уравнение Шредингера для стационарных состояний

В случае, если внешнее поле, в котором движется частица, не зависит от времени, то:

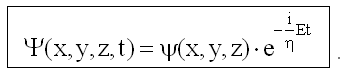
Здесь E - полная энергия частицы, которая в стационарном состоянии сохраняется. Волновая функция Ψ распадается на произведение двух сомножителей. Первый сомножитель ψ(x, y, z) - координатная волновая функция. Второй сомножитель, дает временную зависимость волновой функции Ψ. Эта зависимость универсальна, т.е. не зависит от конкретного вида функции U(x, y, z), задающей потенциальную энергию.

Подставим в уравнение Шредингера (28) волновую функцию После дифференцирования по t и сокращения на экспоненту, получим дифференциальное уравнение для координатной волновой функции ψ(x, y, z):

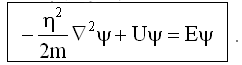
Это уравнение называют уравнением Шредингера для стационарных состояний.

Отметим, что квадраты модулей полной Ψ и координатной ψ волновых функций совпадают. Действительно:

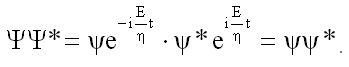
28.2. Уравнение Шредингера для систем взаимодействующих частиц

Для системы N взаимодействующих частиц волновая функция является функцией 3N координат и времени t, т.е.

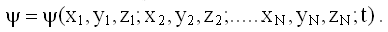
Оператор Лапласа, деленный на массу заменяется на сумму соответствующих выражений для каждой частицы, т.е.

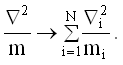
В качестве U записывается потенциальная энергия взаимодействия частиц, т.е.

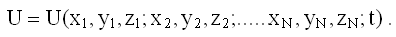
Решение получающегося уравнения представляет большие математические трудности, которые возрастают с ростом числа частиц N. В дальнейшем мы будем рассматривать только стационарное уравнение Шредингера для одной частицы (28.1), причем ограничимся простейшими потенциальными полями.

28.3. Понятия об операторах физических величин

Уравнение Шредингера для стационарных состояний (28.1) можно записать в следующем, операторном виде:

здесь  - гамильтониан частицы, или оператор Гамильтона. Оператор Гамильтона  получается из функции Гамильтона, которая есть сумма кинетической энергии частицы, выраженной через импульс, и ее потенциальной энергии, т.е.

Если в этом выражении импульс частицы p заменить на оператор импульса то из функции Гамильтона получим оператор Гамильтона . Оператор импульса частицы в квантовой механике выглядят следующим образом:

следовательно гамильтониан  для одной частицы будет иметь следующий вид:

Легко убедиться, что после подстановки полученного выражения для  в уравнение Шредингера в операторном виде мы получим уравнение Шредингера в виде (28.1).

28.4. Решение уравнения Шредингера для свободной частицы

Для свободной частицы потенциальная энергия U ≡ 0. Уравнение Шредингера (28.1) в этом случае выглядит следующим образом:

Для частицы, движущейся вдоль оси х, волновая функция ψ = ψ(х) и уравнение еще упрощается:

Решением этого уравнения будет экспоненциальная функция:

проверить это легко прямой подстановкой. При этом для энергии E получаем, как и следовало ожидать,

здесь p_x = mv - импульс частицы.

Мы видим, что у свободной частицы энергия E и импульс p_x могут принимать любые значения, т.е. не квантуются.

Полную волновую функцию ψ(x, t) получим, домножив ψ(x) на временной множитель (см. (28.1)):

Это есть ничто иное, как уравнение волны де Бройля (27.2.6).

28.5. Частица в бесконечно глубокой одномерной потенциальной яме

28.5.1. Потенциальная энергия

В случае бесконечно глубокой одномерной потенциальной ямы шириной а потенциальная энергия:

28.5.2. Следствия для ψ(х) из вида потенциальной энергии

Изобразим график U(x). Если частица находится в яме, то ее координата х может изменяться от нуля до a. За пределы ямы частица выйти не может, т.к. там потенциальная энергия бесконечно велика (стенки ямы бесконечно высоки). Значит вероятность обнаружить частицу в любом месте за пределами ямы равна нулю (dw = 0).

В одномерном случае из (27.2.7) получим:

Откуда следует, что за пределами ямы волновая функция ψ тождественно обращается в ноль.

28.5.2.1. Граничные условия

Из условия непрерывности волновой функции следует, что внутри ямы она должна так зависеть от координаты х, чтобы обращаться в ноль на границах ямы. Значит граничные условия на волновую функцию ψ будут иметь следующий вид:

28.5.3. Вид уравнения Шредингера внутри ямы

Внутри ямы U ≡ 0 и уравнение Шредингера будет иметь такой же вид, как и в (28.4), т.е.

или

Так как , то для коэффициента при ψ имеем:

Откуда энергия частицы:

Здесь k = p / η - волновое число.

В результате уравнение Шредингера примет вид хорошо известного нам дифференциального уравнения (14.2.6):

28.5.3.1. Решение уравнения Шредингера внутри ямы

Решением этого уравнения, как известно (14.2.7), являются гармонические функции (синус или косинус) и мнимая экспонента (28.4). Здесь нам удобнее взять функцию синус с нулевой начальной фазой. Тогда ψ(x) - волновая функция частицы, будет иметь следующий вид:

Постоянная С будет найдена позднее (28.5.3.4) из условия нормировки (27.2.7).

28.5.3.2. Квантование волнового числа как следствие граничных условий

Т.к. sin 0 = 0, то граничное условие на левой границе (ψ(0) = 0) автоматически выполняется. Потребуем выполнения граничного условия на правой границе:

Это граничное условие будет выполнено, если

Значение целого числа n = 0 хотя и удовлетворяет граничному условию, но оно тождественно обращает волновую функцию в ноль (отсутствие частицы в яме!) и поэтому не годится.

Отрицательные значения n не приводят к появлению новых состояний: при изменении знака n меняется знак ψ, тогда как вероятность  не меняется.

В результате мы получили, что вследствие граничных условий волновое число k может принимать лишь дискретные значения:

где квантовое число n принимает любые положительные целые значения, начиная с 1. С аналогичной ситуацией мы уже встречались при рассмотрении колебаний струны, закрепленной с двух концов (15.5.3).

28.5.3.3. Квантование энергии

С волновым числом k связана энергия частицы E (28.5.3). Следовательно, квантование волнового числа приводит к квантованию энергии частицы в потенциальной яме:

Подставляя сюда k_n из (28.5.3.2), получим формулу для стационарных состояний энергии частицы в одномерной бесконечно глубокой потенциальной яме шириной a:

Схема энергетических уровней частицы в яме выглядит следующим образом:

Расстояния между соседними уровнями:

Оценим ΔE_n для молекулы (m ~ 10^-26 кг), находящейся в сосуде размером a ~ 0,lм.

Расстояния между уровнями в этом случае столь малы, что их дискретность совершенно несущественна. Ситуация меняется, если аналогичную оценку сделать для электрона (m_e = 9,1·10^-31 кг), локализованного в области порядка атомных размеров (a ~ 10^-10 м).

В этом случае:

и дискретность уровней будет определять поведение частицы.

28.5.3.4. Нормировка волновых функций

Условие нормировки (27.2.7) для нашей волновой функции (28.5.3.1) имеет следующий вид:

Интеграл равен a/2, значит

Подставляя константу C в волновую функцию (28.5.3.1) и учитывая условия квантования для волнового числа k, получим нормированные волновые функции для частицы в бесконечно глубокой одномерной потенциальной яме:

Каждая из этих волновых функций задает квантовое состояние частицы с квантовым числом n.

28.5.3.5. Плотность вероятности обнаружения частицы

В соответствии с вероятностным смыслом волновой функции (27.2.7) вероятность dw_n обнаружить нашу частицу в интервале от x до x+dx, если она находится в квантовом состоянии ψ_n, дается следующим выражением:

Плотность вероятности

На следующем рисунке приведены графики волновых функций первых двух квантовых состояний и соответствующие графики плотности вероятности :

Из графика плотности вероятности для состояния с n = 2 видно, что точно посередине ямы частица не может быть обнаружена, т.к. там ψ₂² = 0. По классическим же представлениям частица должна была двигаться равномерно внутри ямы, отражаясь от ее стенок. Ясно, что при этом все положения частицы в яме равновероятные.

28.6. Частица в бесконечно глубокой трехмерной потенциальной яме

Рассмотрим частицу, находящуюся в кубе со стороной L. Потенциальная энергия U частицы внутри куба равна нулю, а вне куба U = ∞, так что покинуть переделы куба частица не может.

Задача о частице в такой трехмерной яме не намного сложнее, чем задача о частице в одномерной яме (28.5).

Уравнение Шредингера для частицы внутри трехмерной ямы будет иметь вид:

Введя как и в (28.5.3) волновое число

получим

Нетрудно убедиться прямой подстановкой, что решением этого уравнения будет функция

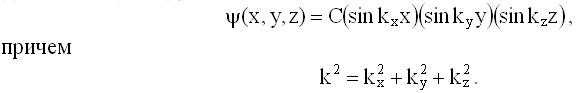
Здесь k_x, k_y, k_z - компоненты волнового вектора . Граничные условия аналогичны (28.5.2.1), они требуют обращения в нуль волновой функции на всех границах потенциальной ямы, т.е. на плоскостях

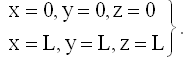
При x = 0, y = 0, z = 0 граничные условия выполняются автоматически. Из граничных условиях при x = L, y = L, z = L следует аналогично (28.5.3.2), что компоненты волнового вектора квантуются:

Отсюда следует квантование энергии частицы, т.к.

Подставляя k_x, k_y, k_z, получим значение энергии частицы в квантовом состоянии, заданном набором квантовых чисел (n_x, n_y, n_z).

28.6.1. Вырождение уровней энергии

Отметим, что одному и тому же значению энергии E в трехмерной яме соответствуют, вообще говоря, несколько разных комбинаций квантовых чисел n_x, n_y, n_z. Например, три комбинации

1)     n_x = 2, n_y = 1, n_z = 1;

2)     n_x = 1, n_y = 2, n_z = 1;

3)     n_x = 1, n_y = 1, n_z = 2;

дают одно и то же значение энергии E, но эти комбинации соответствуют различным волновым функциям, т.е. различным квантовым состояниям. Уровень энергии, отвечающий различным квантовым состояниям, называется вырожденным. Квантовые состояния с одинаковой энергией также называются вырожденными. В приведенном примере вырождение трехкратное. Уровень с минимальной энергией не вырожден. Ему соответствует единственная комбинация квантовых чисел:

n_x = 1, n_y = 1, n_z = 1.

Сибирская государственная геодезическая академия (СГГА), 2006.