ФИЗИКА в конспективном изложении. Часть 3

Содержание Назад Далее

 

КВАНТОВАЯ МЕХАНИКА

28. Уравнение Шредингера. Элементы квантовой механики

28.7. Атом водорода

28.7.1. Уравнение Шредингера для атома водорода

В (26.4) мы разобрали боровскую теорию атома водорода, основанную на постулатах Бора и условии стационарных состояний атома (26.1.6).

Уравнение Шредингера, примененное к атому водорода, позволяет получить результаты боровской теории атома водорода без привлечения постулатов Бора и условия квантования. Квантование энергии возникает как естественное условие, появляющееся при решении уравнения Шредингера, в некотором смысле аналогичное причине квантования энергии для частицы в потенциальной яме (28.5.3.2). Применить стационарное уравнение Шредингера (28.1) к атому водорода это значит:

а) подставить в это уравнение выражение для потенциальной энергии взаимодействия электрона с ядром

б) в качестве m подставить m_e - массу электрона (если пренебречь, как и в (26.4), движением ядра).

После этого получим уравнение Шредингера для атома водорода:

Так как потенциальная энергия зависит только от r, решение уравнения удобно искать в сферической системе координат: r, θ, φ.

Волновая функция в этом случае будет функцией от r, θ и φ, т.е.

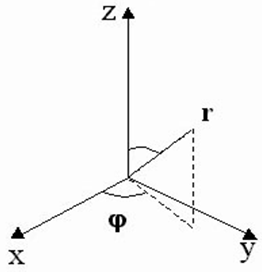
Оператор Лапласа  необходимо записать в сферических координатах, т.е. выразить через производные по r, θ и φ. Мы не будем этого делать, поскольку получение решения уравнения Шредингера для атома водорода не входит в программу курса общей физики. Приведем лишь результаты.

 

28.7.2. Квантование энергии

Оказывается, что решение уравнения Шредингера для атома водорода существует при следующих условиях:

а) при любых положительных значениях полной энергии (E > 0). Это так называемые несвязанные состояния электрона, когда он пролетает мимо ядра и уходит от него на бесконечность;

б) при дискретных отрицательных значениях энергии

Эта формула совпадает с полученной Бором формулой для энергии стационарных состояний атома водорода (26.4). Целое число n называют главным квантовым числом.

28.7.3. Квантовые числа

Волновые функции электрона ψ_nlm(r, θ, φ) определяются тремя целочисленными параметрами: n, l, m_e. Эти целые числа называются квантовыми числами:

n - главное квантовое число, оно, как мы знаем (28.7.2), определяет значение энергии E_n, n=1,2,3...

l - азимутальное (орбитальное) квантовое число, оно определяет L - модуль момента импульса электрона.

При заданном n азимутальное квантовое число может принимать следующие значения:

l = 0, 1, ... (n - 1), всего n значений.

Следовательно, из уравнения Шредингера вытекает, что момент импульса электрона в атоме водорода квантуется и может принимать n значений. Так при n = 1 азимутальное квантовое число может принимать единственное значение l = 0. При n = 2 возможны значения l = 0,1.

m_l - это магнитное квантовое число.

Из уравнения Шредингера так же следует, что проекция момента импульса L на выбранное направление в пространстве, скажем, ось z, также квантуется. Величина этой проекции, L_z, связана с квантовым числом m_l.

L_z - проекция  момента импульса электрона на ось z, может принимать следующие значения:

При заданном l магнитное квантовое число m_l может принимать следующие значения:

всего 2l+1 значений.

Значит, при заданной главным квантовым числом n энергии E_n возможны n значений азимутального квантового числа (от l = 0 до n - 1) и 2l+1 значений магнитного квантового числа m_l. Таким образом, при заданном n число различных волновых функций ψ_nlm, отвечающих заданной энергии E_n, будет равно

и уровень энергии E_n будет вырожден (28.6.1) с кратностью n².

28.7.4. Спектроскопические обозначения момента импульса

В атомной физике применяют заимствованные из спектроскопии условные обозначения состояний электрона с различными значениями момента импульса:

l = 0 -      s-состояние;

l = 1 -      p-состояние;

l = 2 -      d-состояние;

l = 3 -      f-состояние;

затем идут g, h и дальше в алфавитном порядке.

Значение главного квантового числа n указывают перед буквой, являющейся условным обозначением азимутального квантового числа l.

Например, 1s-состояние - это состояние с главным квантовым числом n = 1 и азимутальным квантовым числом l = 0 (на это указывает буква s).

28.7.5. Спектры атома водорода в теории Шредингера

Появление в шредингеровской теории атома водорода, в отличие от теории Бора (26.4), квантования момента импульса L и его проекции L_z (28.7.3) объясняет некоторые особенности спектров излучения и поглощения атома водорода, которые не могли быть объяснены теорией Бора. Для пояснения этих особенностей изобразим схему уровней атома водорода, на которой учтено вырождение уровней по азимутальному квантовому числу l.

28.7.5.1. Схема уровней атома водорода с учетом вырождения по l. Правило отбора

На приведенной схеме по вертикали отложена полная энергия E_n электрона в атоме водорода (как и в (26.4.1)), выраженная в электронвольтах и значения главного квантового числа n. По горизонтали отложены дискретные значения азимутального квантового числа l (28.7.3), вместе с их спектроскопическими обозначениями (28.7.4).

Линии, соединяющие энергетические уровни, обозначают разрешенные правилом отбора переходы электрона с одного энергетического уровня на другой. При этом или испускаются или поглощаются фотоны соответствующих энергий ε = E_n - E_m.

Правило отбора связано с тем, что фотон обладает собственным моментом импульса. При излучении света фотон уносит момент импульса из атома, а при поглощении - приносит. Поэтому, вследствие закона сохранения момента импульса, момент импульса атома в процессах излучения и поглощения фотонов изменяется. Оказывается, с наибольшей интенсивностью идут такие переходы, в которых выполняется следующее правило отбора: Δl = ±l

Это правило отбора справедливо для так называемых дипольных переходов. Оно запрещает, например, дипольный переход электрона из состояния 2s в состояние 1s, разрешенный законом сохранения энергии. Поэтому электрон может сравнительно долго находиться в состоянии 1s, если он туда попадает. Такое состояние называется метастабильным.

28.7.6. Волновая функция основного состояния атома водорода

Для основного состояния атома водорода квантовые числа n, l, m_l имеют следующие значения:

n = 1, l = 0, m_l = 0.

Это состояние обозначает 1s (28.7.4). Уравнение Шредингера имеет для 1s состояния решение ψ_nml = ψ₁₀₀₁ которое зависит только от расстояния r между ядром и электроном:

Здесь  - первый боровский радиус (см. (20.4)).

28.7.6.1. Вероятность обнаружить электрон 1s состояния

В соответствии с вероятностным смыслом волновой функции (27.2.7) вероятность dw обнаружить электрон в объеме dV:

Отметим, что dw зависит от выбранной нами формы элементарного объема dV.

Если взять dV в форме прямоугольного параллелепипеда, т.е.  и обозначить через dw_ соответствующую вероятность, то

В этом случае плотность вероятности обнаружить электрон в объеме параллелепипеда dV = dx, dy, dz будет равна

Плотность вероятности имеет максимальное значение (1/π₀³) при r = 0, график этой функции изображен на рисунке.

Так как волновая функция 1s состояния зависит только от r, то обычно элемент объема dV берут в виде сферического слоя радиуса r и толщиной dr. Как известно из геометрии, объем такого сферического слоя dV = 4πr²dr. Обозначим через dw₀ соответствующую вероятность, тогда

Эта функция равна нулю при r = 0 и r → ∞. При r = r₀ она имеет максимум, положение которого соответствует первой боровской орбите.

28.7.7. Дальнейшее развитие представлений о спектрах атома водорода

Так как стационарные значения энергии атома водорода в теории Бора и в теории Шредингера совпадают, то в первом приближении из теории Шредингера следуют такие же спектры излучения и поглощения, как и в теории Бора (26.4.1.1). Однако, шредингеровская теория атома водорода позволяет учесть влияние на энергетические уровни взаимодействия орбитального и спинового (28.8) моментов импульса электрона (тонкая структура спектра). Кроме того шредингеровская теория позволяет учесть влияние на спектры магнитного поля (эффект Зеемана) и электрического поля (эффект Штарка). Учет взаимодействия спиновых магнитных моментов ядра и электрона приводит к сверхтонкому расщеплению уровня 1s атома водорода на два подуровня. Переход электрона между этими подуровнями приводит к излучению (или поглощению) радиоволн с длиной волны λ = 21 см. Такое излучение испускается межзвездным водородом в галактиках. Изучая это излучение с помощью радиотелескопов, астрономы получают много полезной информации.

 

28.8. Спин электрона

Как уже упоминалось (28.7.6), спектральные линии атома водорода обнаруживают тонкую структуру. Тонкая структура присуща спектрам всех атомов. Для объяснения причин возникновения тонкой структуры американские физики Гаудсмит и Уленбек выдвинули в 1925 г. гипотезу о том, что электрон обладает собственным моментом импульса - спином L_s, не связанным с движением электрона в пространстве. Модуль собственного момента импульса определяется спиновым квантовым числом s:

Для электрона s  = 1/2.

Проекция спина на ось z, L_sz, квантуется

здесь m_s - магнитное спиновое квантовое число. Для электрона

28.8.1. Квантовое состояние электрона в атоме

Квантовое состояние электрона в любом атоме задается четырьмя квантовыми числами:

главным n (n = 1, 2, 3...);

азимутальным l  (l = 0, 1, 2, ... n-1);

магнитным m_l (m_l = -l,... -1, 0, 1 ... +l);

спиновым m_s (m_s = +1/2, -1/2).

О физическом смысле первых трех квантовых чисел сказано в (28.7.3), о последнем, m_s, - в (28.8).

Энергия состояния зависит главным образом от квантовых чисел n и l. Есть слабая зависимость энергии от m_l и m_s, т.к. эти квантовые числа определяют взаимодействие между орбитальным и спиновым магнитными моментами электрона. Это взаимодействие приводит к появлению тонкой структуры спектров.

28.8.2. Принцип Паули. Фермионы и бозоны

Принцип Паули утверждает, что в квантовой системе две тождественные частицы с полуцелым спином не могут находиться в одном и том же квантовом состоянии, т.е.

Этот принцип был сформулирован в 1925 г. швейцарским физиком В. Паули для электронов в атоме, а затем распространен на любые частицы с полуцелым спином - фермионы. К фермионам относятся электрон, протон, нейтрон.

Частицы с целым спином носят название бозонов. К бозонам относятся фотон (спин s = 1), мезон, составные частицы из четного числа фермионов, например, α-частица - ядро атома ⁴₂He. Бозоны могут находиться в одинаковом квантовом состоянии в неограниченном количестве.

28.8.2.1. Физические основы периодической системы элементов Д. И. Менделеева

Принцип Паули, примененный к атому, утверждает, что в любом атоме не может быть двух электронов с одинаковым набором квантовых чисел n, l, m_l, m_s (28.8.1). Исходя из этого принципа, можно понять построение периодической системы элементов Д. И. Менделеева. Химические свойства атомов определяются внешними (валентными) электронами. Заполнение электронами квантовых состояний в атоме при учете принципа Паули приводит к периодически изменяющемуся с ростом зарядового числа z характеру заполнения квантовых состояний валентными электронами. Этим и объясняется периодическое повторение химических свойств элементов. Поясним сказанное на примере первых одинадцати элементов периодической системы элементов Менделеева.

У водорода (H) один электрон, зарядовое число z = 1, т.е. заряд ядра равен элементарному заряду +e. Состояния атома водорода были нами разобраны в (26.4) и в (28.7). В основном состоянии атома водорода квантовое число n = 1, l = 0, m_l = 0. Квантовое число m_s может быть как +1/2, так и -1/2. Говорят, что электронная конфигурация основного состояния атома водорода 1s (28.7.4). Энергия связи 1s электрона равна 13,6 эВ.

У атома гелия (He) зарядовое число z = 2 и два электрона. Наборы квантовых чисел электронов отличаются квантовым числом m_s; у одного из электронов m_s=+1/2, у другого m_s=-1/2 (при n = 1, l = m_l = 0). Электронная конфигурация гелия 1s². Это означает, что в 1s состоянии находятся два электрона с противоположными спинами. Электроны, имеющие одинаковое главное квантовое число n, образуют оболочку. В гелии оболочка с n = 1 заполняется полностью, поэтому гелий химически инертен. Энергия ионизации гелия равна 24,6 эВ.

Литий (Li) имеет зарядовое число z = 3 и, соответственно, три электрона. Электронная конфигурация лития 1s²2s, это значит, что третий электрон находится на второй оболочке, т.к. опуститься на первую ему запрещает принцип Паули. Энергия связи этого электрона невелика (5,4 эВ) и литий химически активен.

Бериллий (Be). У него четыре электрона заполняют 1s и 2s состояния, находясь в них с противоположными спинами. Электронная конфигурация бериллия 1s²2s².

От бора (B) до неона (Ne) происходит последовательное заполнение 2p состояний (n = 2, l = 1, m_l = -1, 0 +1, m_s = ╠1/2 - всего 6 состояний).

У неона электронная конфигурация 1s²2s²2p⁶, здесь завершено заполнение оболочки с n = 2, поэтому неон, как и гелий, химически инертен.

Натрий (Na). У него одиннадцать электронов, одиннадцатый начинает новую оболочку, попадая в 3s состояние. Энергия связи этого электрона невелика (5,1 эВ) и натрий, как и литий, химически очень активен.

На этом мы остановимся. Принцип заполнения электронами состояний в первом приближении понятен из разобранных примеров. В заключении приведем схему заполнения электронами квантовых состояний первых одиннадцати атомов.

На этой схеме стрелочками обозначены направления проекций спинов электронов на ось z. Стрелка вверх соответствует значению спинового квантового числа  m_s=+1/2, стрелка вниз означает, что m_s=-1/2.

28.9. Молекула

Молекула состоит из атомов, связанных друг с другом за счет валентных электронов (22.1.2). Квантовая механика позволяет выяснить физическую природу этой химической связи.

Молекула представляет собой связанную систему ядер и электронов, между которыми действуют электростатические силы. Кроме электростатических сил в квантово-механическом рассмотрении молекулы необходимо учитывать принцип Паули (28.8.3), который приводит к существованию дополнительного обменного взаимодействия.

Различают два типа связи в молекулах: ковалентную и полярную.

28.9.1. Ковалентная связь

Ковалентная (гомеополярная) связь осуществляется за счет обобществления электронов, принадлежащих двум атомам.

Простейшей молекулой с ковалентной связью является молекула водорода. В 1927 г. немецкие физики Гайтлер и Лондон решили уравнение Шредингера для системы, состоящей из двух протонов (ядра атома водорода) и двух электронов. Оказалось, что энергия E молекулы водорода по разному зависит от расстояния r между ядрами для случаев параллельной и антипараллельной ориентации спинов электронов. График этой зависимости приведен на рисунке, из которого видно, что связанное состояние с E < 0 возможно лишь при антипараллельной ориентации спинов.

За начало отсчета энергии молекулы E на графике принята энергия двух изолированных атомов. При r = r₀ график с антипараллельными спинами имеет минимум, определяющий равновесное положение ядер в молекуле водорода. Электроны большую часть времени проводят между ядрами, таким образом, положительные ядра притягиваются к отрицательному "электронному облаку".

 

28.9.2. Ионная связь

Ионная (гетерополярная) связь обусловлена переходом валентных электронов с одного атома на другой с образованием положительных и отрицательных ионов с электростатическим притяжением между ними.

Характерный пример ионной связи - NaCl (поваренная соль). Такого типа связь будет и у NaF, на схеме заполнения электронных состояний, приведенной в (28.8.2.1) видно, что у фтора (F) не заполнено одно квантовое состояние 2p, а у натрия (Na) один валентный электрон находится в состоянии 3s, где он сравнительно слабо связан со своим атомом. Этот 3s электрон натрия и переходит в 2p состояние атома фтора. Таким образом, атом Na становится положительным ионом, а атом F - отрицательным, поэтому они и притягиваются друг к другу.

28.9.3. Понятие об энергетических уровнях молекул

Энергия изолированной молекулы может быть приближенно представлена в следующем виде: E ≈ E_эл + E_кол + E_вр,

здесь E_эл - электронная энергия, она обусловлена электронной конфигурацией в молекуле;

E_кол - энергия колебания ядер относительно центра масс атома;

E_вр - энергия вращения ядер относительно центра масс атома.

Порядки величин E_эл, E_кол и E_вр следующие:

Каждая из составляющих энергии E_эл, E_кол и E_вр квантуется. Ввиду большого различия в их величинах изобразить энергетическую схему уровней молекулы в масштабе не представляется возможным. На рисунке изображены два электронных уровня E_эл1 и E_эл2 и система колебательных и вращательных уровней.

28.9.3.1. Объяснение температурной зависимости теплоемкостей газов

В (24.3.3.4) обсуждались графики экспериментальных зависимостей теплоемкости C_V для двух газов: одноатомного аргона (Ar) и двухатомного водорода (H₂). Ход графика для аргона соответствовал предсказаниям классической теории теплоемкости: у одноатомного газа три степени свободы (i = 3), соответственно  во всем диапазоне температур. Двухатомный водород имеет i = 7 (3 поступательные, 2 вращательные, 2 колебательные степени свободы, см. (22.2.9)), классическая теория дает для него значение C_V = (7/2)R. Однако, как показывает опыт (24.3.3.4), водород ведет себя как газ с переменным числом степеней свободы. Они как бы "вымораживаются": при низких температурах i = 3, затем при T > 100K число степеней свободы плавно(!) увеличивается и достигает 5 при T ≈ 400K. Затем до T ≈ 800K число степеней свободы остается постоянным, а дальше опять плавно растет до значения i = 7.

Такое поведение теплоемкости становится понятным если учесть квантование вращательного и колебательного движений молекулы. Поступательное движение не квантуется и его вклад в теплоемкость (i = 3) присутствует всегда. При низких температурах, когда средняя энергия теплового движения молекулы (ε ~ kT) меньше, чем квант энергии вращательного движения (см. схему уровней в (28.9.3)), тепловое движение не способно возбудить вращение молекулы и она ведет себя как частица без внутренней структуры с числом степеней свободы i = 3. Затем, с ростом T, у наиболее энергичных молекул начинают возбуждаться вращательные степени свободы, этим объясняется плавный рост теплоемкости, соответствующий появлению нецелых значений числа i. Колебательные степени свободы возбуждаются при более высоких температурах, т.к. расстояние между колебательными уровнями значительно больше, чем расстояние между вращательными.

Сибирская государственная геодезическая академия (СГГА), 2006.