ФИЗИКА в конспективном изложении. Часть 3

Содержание Назад Далее

 

КВАНТОВАЯ МЕХАНИКА

29. Квантовая теория свободных электронов в металле

Валентные электроны в металле могут довольно свободно перемещаться в пределах объема металлического образца. Потенциальная энергия электрона в пределах образца металла приблизительно постоянна, но для выхода электрона из металла надо совершить работу против сил электростатического притяжения отрицательного электрона к ионному остатку.

Таким образом, валентные электроны металла находятся в потенциальной яме. Глубина этой ямы - работа выхода электронов из металла A - составляет несколько электронвольт. При низких температурах, когда тепловое движение не способно удалить электрон из металла, потенциальную яму можно считать бесконечно глубокой. Мы начнем рассмотрение поведения свободных (валентных) электронов в металле с самой простой модели: модели одномерной бесконечно глубокой потенциальной ямы (28.5) при T = 0. Затем обобщим результаты на случай более реалистичной модели бесконечно глубокой трехмерной ямы (28.6). После чего рассмотрим поведение свободных электронов в металле (электронный газ) при T > 0, для чего нам потребуются элементы квантовой статистики Ферми-Дирака.

29.1. Электронный газ в модели одномерной бесконечно глубокой ямы

Поведение одной частицы в бесконечно глубокой одномерной яме было разобрано в (28.5). Теперь мы хотим разместить в этой яме N свободных электронов. При этом взаимодействием между электронами мы пренебрегаем, но обязательно должны учесть принцип Паули (28.8.2). В нашем случае квантовыми числами, задающими состояние электрона, будут n (28.5.3.2) и спиновое квантовое число m_s, которое для электрона может принимать два значения, m_s = ±1/2 (28.2). Принцип Паули утверждает, что в одномерной яме не может быть двух электронов с одинаковыми квантовыми числами n и m_s. Так как m_s принимает два значения, то на каждом энергетическом уровне в одномерной яме сможет разместиться не больше двух электронов.

На рисунке изображена одномерная, бесконечно глубокая потенциальная яма, в которой размещены шесть электронов (N = 6) при T = 0. Первые три энергетических уровня заняты, все остальные, начиная с четвертого (n = 4), свободны.

 

29.1.1. Энергия Ферми для одномерной ямы

Ферми Э. (1901-1954) - итальянский физик.

Энергия Ферми E_F(0) - это энергия электронов на высшем, еще заполненном уровне при T = 0. На нашем рисунке (29.1) энергия Ферми при N = 6 равна энергии третьего энергетического уровня. В реальных ситуациях число электронов N имеет порядок числа Авогадро (22.1.4), т.е. N ~ N_A. Выражение для энергии Ферми при T = 0, E_F(0), получим, приравняв квантовое число n в формуле для энергии стационарных состояний частицы в одномерной бесконечно глубокой потенциальной яме (28.5.3.3) половине числа частиц, т.е. n = N/2 (т.к. на каждом уровне - два электрона). Тогда получим:

Как мы видим, энергия Ферми при T = 0, E_F(0) зависит от числа занятых электронами состояний. В одномерной яме число занятых состояний N (одно состояние - один электрон) (!) равно удвоенному значению квантового числа n. В других ситуациях подсчет числа состояний, доступных микрочастицам, более сложен. Так в трехмерной яме уровни энергии вырожденны (28.6.1) и уже нельзя считать, что на каждом энергетическом уровне могут находиться по два электрона (но по-прежнему в одном состоянии ? 1 электрон, т.к. обязательно соблюдается принцип Паули (28.8.2)).

29.2. Фазовое пространство. Подсчет числа состояний

Для задания состояния рассматриваемой системы частиц в классической физике вводят фазовое пространство, объединяющее координаты и импульсы всех частиц системы.

29.2.1. Фазовое пространство и фазовая ячейка в одномерном случае

Для одной частицы, совершающей одномерное движение (частица в одномерной яме), фазовое пространство представляет из себя две взаимно-перпендикулярные оси, по которым откладывается координата x и соответствующий ей импульс p. В квантовой механике появляются ограничения на возможные значения импульса, связанные с квантованием волнового числа k (28.5.3.2). Для частицы в яме шириной a

Так как по соотношению де Бройля (27.2)

то импульсы тоже квантуются:

Здесь

Как отмечалось в (28.5.3.2) положительные и отрицательные числа n соответствуют одному и тому же стационарному состоянию, но в фазовом пространстве положения точек, имеющих разные по знаку импульсы, будут разными. Объемом нашего двухмерного пространства ΔГ называют произведение ΔpΔx, т.е.

здесь Δp - интересующий нас интервал изменения импульса, а Δx - интервал изменения координаты.

Найдем Г_эл - элементарный объем, занимаемый в фазовом пространстве одним квантовым состоянием частицы, находящейся в одномерной бесконечно глубокой яме (спиновое квантовое число здесь не учитывается). Из рисунка видно, что для одного квантового состояния

Двойка появляется из-за того, что одному состоянию соответствуют два значения импульса, отличающиеся знаком.

Очевидно, что Δx = a, то

Таким образом, одно квантовое состояние частицы, находящейся в одномерной бесконечно глубокой потенциальной яме, занимает в фазовом пространстве одну элементарную ячейку размером h.

29.2.1.1. Подсчет числа квантовых состояний Z в одномерном случае (без учета спина)

Для подсчета числа квантовых состояний Z в фазовом объеме ΔГ очевидно необходимо поделить фазовый объем ΔГ на объем элементарной ячейки h, т.е.

Здесь мы пока отвлекаемся от наличия у частицы спина.

29.2.2. Подсчет числа квантовых состояний в трехмерном случае

В трехмерном случае фазовое пространство для одной частицы - это шестимерное пространство, по осям которого откладываются три координаты x, y, z и три компоненты импульса p_x, p_y, p_z частицы. Объем фазового пространства кубической формы , здесь ΔV - обычный пространственный объем области, в которой находится частица. Объем элементарной фазовой ячейки в трехмерном случае можно найти из соображений, аналогичных тем, что были изложены в (29.2.1) для одномерного случая. В результате получим, что

Для числа состояний Z в трехмерном случае имеем:

Здесь, как и в одномерном случае (29.2.1.1), мы пока отвлекаемся от наличия у частицы спина.

Для электронов с учетом спина число квантовых состояний будет в два раза больше, т.е.

29.3. Электронный газ в модели бесконечно глубокой трехмерной потенциальной ямы

29.3.1. Энергия Ферми в трехмерной яме

Как и в одномерном случае (29.1.1) энергия Ферми E_F(0) - это энергия электронов на высшем еще заполненном уровне при T = 0. При T = 0 в соответствии с принципом Паули (28.8.2) каждое квантовое состояние с E < E_F(0) будет занято одним из общего числа N электронов.  Значит, для нахождения E_F(0), нам надо найти зависимость числа состояний Z от энергии E, затем приравнять число состояний с энергией числу частиц и выразить из этого равенства E_F(0). Реализуем последовательно эту программу.

29.3.1.1. Число состояний Z в фазовом объеме ΔГ

В соответствии с (29.2.2)

здесь двойка учитывает две возможные ориентации спина.

29.3.1.2. Фазовый объем ΔГ состояний с импульсом p < p_F(0)

Так как полная энергия E электронов внутри потенциальной ямы равна кинетической, то

Значит состояния с - это состояния, у которых модуль импульса электронов лежит в пределах от нуля до В подпространстве импульсов этим состояниям соответствует сфера радиусом p_F(0). Умножив "объем" этой сферы  на объем ямы V получим интересующий нас объем фазового пространстве ΔГ, т.е.

29.3.1.3. Число состояний Z(E)

Из (29.3.1.1) и (29.3.1.2) получим число состояний Z(p) с учетом спина:

29.3.1.4. Плотность состояний g(E)

В дальнейшем нам потребуется выражение для числа состояний на единичный энергетический интервал - плотность состояний g(E).

Очевидно, что

Подставив Z(E) из (29.3.1.3), получим

29.3.1.5. Энергия Ферми E_F(0) для электронного газа в трехмерной яме

Приравняв Z(E_F) (29.3.1.3) числу электронов в яме N, получим

Выразим отсюда E_F(0):

здесь  - концентрация электронов.

Выразив h через η = h/2π, получим окончательную формулу для E_F(0) - энергии Ферми для электронного газа в трехмерной потенциальной яме:

29.3.1.6. Температура Ферми T_F

Температура Ферми T_F - это отношение энергии Ферми E_F(0) к постоянной Больцмана k, т.е.

29.3.1.7. Оценка E_F(0) и T_F

Концентрация свободных электронов в металле порядка 10²⁸÷10²⁹ м^-3. Для n = 5·10²⁸ м^-3 получим:

Для T_F из (29.3.1.6) получим:

29.3.2. Электронный газ при T > 0. Распределение Ферми-Дирака

На приведенных выше рисунках изображена одномерная потенциальная яма, заполненная электронным газом; на рис. а) при T = 0, на рис. б)  при T > 0. Слева от потенциальной ямы изображены графики зависимости среднего по времени числа электронов в одном квантовом состоянии - <n(E)> - от энергии электронов E. Энергия E отложена по вертикальной оси, проходящей вдоль левой границы ямы, сама функция <n(E)> отложена по горизонтальной оси, направленной влево.

При T = 0K электроны занимают все доступные им состояния с наинизшей энергией. В соответствии с принципом Паули (28.8.2) в каждом квантовом состоянии может находиться не более одного фермиона, поэтому все нижние квантовые состояния до энергии E_F(0) (см. (29.1)) заняты. Таким образом, график функции <n(E)> представляет из себя ступеньку:

<n(E)> = 1 при E < E_F(0) и <n(E)> = 0 при E > E_F(0).

При нагревании металла часть электронов, энергия которых была близка к энергии Ферми, переходят в состояния с большей энергией, частично освобождая квантовые состояния с энергией E < E_F(0): ступенька графика <n(E)> размывается.

29.3.2.1. Распределение Ферми-Дирака для <n(E)>

Аналитическую зависимость среднего числа ферминов в одном квантовом состоянии от их энергии и температуры получили итальянский физик Э. Ферми и английский физик П. Дирак.

Она имеет следующий вид:

и называется распределением Ферми-Дирака. Параметр E_F, входящий в распределение Ферми-Дирака, называется уровнем Ферми. В статистической физике этот параметр называется химическим потенциалом, его обозначают буквой μ, таким образом μ ≡ E_F.

29.3.2.2. Функция распределения Ферми-Дирака f(E)

Среднее число электронов в одном квантовом состоянии <n(E)> изменяется от нуля до единицы, в этих же пределах изменяется вероятность f(E_i) заполнения данных квантовых состояний.

Таким образом

С учетом того, что , функцию распределения Ферми-Дирака можно записать в таком виде:

29.3.2.3. Условие нормировки функции распределения Ферми-Дирака

Значение уровня Ферми E_F (или химического потенциала μ) определяют из условия нормировки  функции f(E_i): полное число электронов, находящихся во всех квантовых состояниях должно быть равно числу N свободных электронов в рассматриваемом объеме V.

Среднее число электронов в одном квантовом состоянии дается функцией Ферми-Дирака f(E_i). Так как расстояния между соседними уровнями при макроскопических объемах образца малы, то можно считать, что энергия меняется непрерывным образом, т.е. f(E_i) →f(E).

Число квантовых состояний, приходящихся на интервал энергий dE получим, умножив плотность состояний g(E) (29.3.1.4) на dE. Число электронов dN, имеющих энергию в интервале от E до E+dE, получим, умножив f(E) на g(E)dE, т.е.

Наконец, проинтегрировав dN, получим N - полное число электронов в образце:

Это и есть условие нормировки функции распределения Ферми-Дирака.

29.3.2.4. Зависимость E_F от T

Значение E_F (или химический потенциал) можно найти, подставив в условие нормировки f(E) из (29.3.2.2) и g(E) из (29.3.1.4). Однако аналитическое выражение для получающегося интеграла отсутствует. При не очень высоких температурах, таких, что kT << E_F, для уровня Ферми получается приближенное выражение

Здесь E_F(0) определяется формулой, полученной в (29.3.1.5).

29.3.2.5. Анализ функции f(E)

Выпишем функцию распределения Ферми-Дирака в следующем виде:

Нетрудно убедиться, что при E = E_F функция f(E) = 1/2.

Поведение функции f(E) (и электронного газа в металле) зависит от соотношения между температурой металла T и температурой Ферми (29.3.2.3).

При T << T_F (т.е. kT << E_F) электронный газ называют вырожденным и график функции f(E) незначительно отличается от ступени. В самом деле, показатель экспоненты (E - E_F)/kT будет велик по модулю всюду, за исключением интервала энергий, в котором При этом, если E < E_F, то (E - E_F)/kT будет величиной отрицательной и большой по модулю, значит экспонента будет близка к нулю, а f(E)≈1. В случае, если E > E_F, показатель экспоненты будет большой положительной величиной и f(E)≈0.

 Запишем результаты анализа в следующем виде:

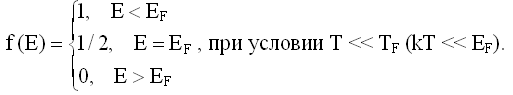
Из оценок, сделанных в (29.3.1.7), T_F ≈ 60000K, значит вплоть до T_пл - температуры плавления металлов, электронный газ вырожден (самый тугоплавкий металл, вольфрам, имеет T_пл ≈ 3693K).

При T >> T_F электронный газ называется невырожденным. В этом случае график функции f(E) идет полого спадая и уже совсем не похож на ступеньку.

29.3.2.6. Графики распределения Ферми-Дирака

На следующем рисунке приведены графики функции f(E) (29.3.2.2) для различных температур.

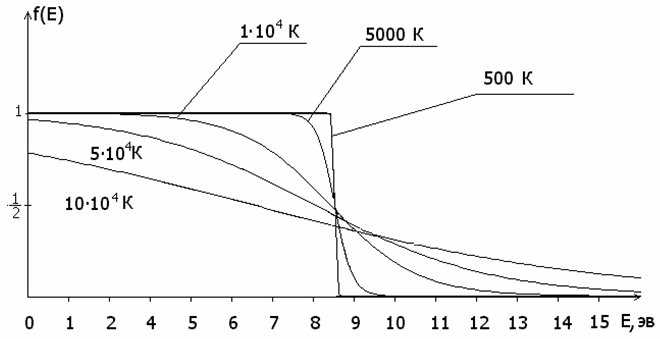
29.3.2.7. "Хвост" функции f(E)

При больших значениях энергии электронов, таких, что E - E_F >> kT, единицей в знаменателе функции f(E) (29.3.2.5) можно пренебречь, тогда для "хвоста" функции f(E) справедлива следующая формула:

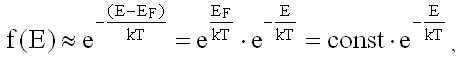
что совпадает с распределением Максвелла-Больцмана (23.4.8).

 

29.4. Результаты квантовой теории электропроводности металла

В (25.6.1) в рамках классической теории электропроводности была получена формула для σ - удельной проводимости:

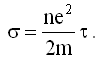
В (25.6.2) было получено, что время свободного пробега

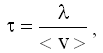
где λ - длина свободного пробега электрона проводимости в металле;
<v> - средняя скорость теплового движения электронов, для которой из распределения Максвелла следует, что В результате из классической теории электропроводности следует, что тогда как опыт дает   (см. (25.6.3)).

Квантовая теория электропроводности дает для σ следующую формулу:

В этой формуле m* - эффективная масса электрона, которая учитывает влияние сил, действующих на электрон со стороны ионных остовов кристаллической решетки. Время свободного пробега τ в квантовой теории определяется как отношение длины свободного пробега λ к v_F - скорости электрона, имеющего энергию вблизи уровня Ферми:

Только те электроны, что находятся вблизи уровня Ферми, участвуют в переносе заряда, остальные - не возмущаются внешним полем. Скорость v_F с большой точностью можно считать независящей от температуры, таким образом температурная зависимость проводимости σ определяется зависимостью от температуры длины свободного пробега λ. Зависимость λ(T) обусловлена, в основном, тепловыми колебаниями атомов кристалла и при не очень низких температурах эта зависимость линейна, т.е. Это и приводит к линейной зависимости удельного сопротивления от температуры, т.е.:

Сибирская государственная геодезическая академия (СГГА), 2006.