ФИЗИКА в конспективном изложении. Часть 3

Содержание Назад Далее

 

КВАНТОВАЯ МЕХАНИКА

29. Квантовая теория свободных электронов в металле

29.5. Термоэлектронная эмиссия

 

Термоэлектронной эмиссией называется испускание электронов нагретыми телами.

 

29.5.1. Работа выхода

Глубина потенциальной ямы U_0, в которой находятся электроны в металлах, порядка 10 эВ (например в цезии U₀ ≈ 3,5 эВ, в бериллии U₀ ≈ 18 эВ). Энергия Ферми, разумеется, меньше, чем U₀ (для цезия E_F = 1,58 эВ, для бериллия E_F = 14,14 эВ).

Наименьшая работа, необходимая для удаления электрона из металла, равна:

Эта работа А называется работой выхода электрона из металла. При T > 0K работу выхода также определяют как разницу между глубиной потенциальной ямы U₀ и уровнем Ферми. Так как уровень Ферми E_F зависит от температуры (29.3.2.4), то величина работы А также немного зависит от температуры.

29.5.2. Электронное облако

При T > 0 имеется некоторое количество электронов, энергия которых достаточна для выхода из металла. Покинуть металл могут те электроны, энергия которых E > U₀ (см. рисунок). Число их пропорционально площади, ограниченной хвостом правого графика и осью энергий:

Около поверхности нагретого металла возникает электронное облако. Это облако и металл находятся в динамическом равновесии: потоки электронов из металла в облако и из облака в металл одинаковы.

29.5.3. Ток насыщения

Пусть поверхность нагретого металла лежит в плоскости x, y, а ось z направлена перпендикулярно поверхности, как изображено на следующем рисунке. Расположим параллельно катоду еще одну металлическую пластину и подадим на нее положительный потенциал.

Возникающее электрическое поле будет создавать направленное движение электронов от катода к аноду - потечет электрический ток. При увеличении положительного потенциала анода электрический ток сначала растет, затем достигает максимального значения. Это значение называется током насыщения. При этом все электроны, покидающие катод за время Δt, увлекаются электрическим полем и достигают за это же время анода.

29.5.4. Формула Ричардсона-Дэшмена для плотности тока насыщения

Плотностью тока, как известно (10.2), называется отношение силы тока к площади поперечного сечения проводника.

При движении носителей заряда со средней скоростью упорядоченного движения <v> плотность тока j связана с концентрацией электронов n и величиной <v> следующим образом (10.2.1):

здесь e - элементарный заряд.

При термоэлектронной эмиссии электроны, покидающие металл, имеют разные скорости. Вклад в плотность тока электронов, вылетающих из катода по направлению к аноду и имеющих компоненту скорости вдоль оси z в интервале от v_z до v_z + dv_z , дается выражением:

Здесь dn_vz = dn_pz - концентрация электронов, имеющих скорость v_z и соответствующий ей импульс p_z = mv_z в указанном выше интервале.

Плотность тока насыщения получим, проинтегрировав dj по p_z от нуля до бесконечности:

Для dn_pz получается следующее выражение:

Здесь 2/h³ возникает при подсчете числа состояний в фазовом объеме dVdp_xdp_ydp_z. Интегрирование по p_x и p_y исключает из рассмотрения движение электронов параллельно поверхности катода. "Хвост" функции распределения Ферми-Дирака (29.3.2.7) должен быть выражен через компоненты импульса электрона в соответствии с равенством:

Здесь учтем, что U₀ - E_F = A (29.5.1). Интегрирование дает следующий результат:

Введя обозначение:

получим формулу Ричардсона-Дэшмена для плотности тока насыщения:

Постоянная В называется константой Ричардсона.

Численное значение константы Ричардсона:

Измеряя на опыте зависимость тока насыщения от температуры, можно экспериментально определить работу выхода электрона А и материал, из которого изготовили катод.

29.6 Бозоны

Бозон - это частица или (квазичастица - как, например, фонон - квант упругих колебаний в твердых телах) с нулевым или целочисленным спином. К бозонам, как уже упоминалось (28.8.2), относятся также фотоны (спин s = 1), составные частицы, состоящие из четного числа фермионов (например, для атома ⁴₂He), куперовские пары электронов, образование которых приводит к сверхпроводимости.

29.6.1. Распределение Бозе-Эйнштейна

Распределение Бозе-Эйнштейна дает <n(E_i)> среднее число невзаимодействующих между собой бозонов в состоянии с энергией E_i, где i - набор квантовых чисел, характеризующих квантовое состояние. Формула распределения Бозе-Эйштейна имеет следующий вид:

где μ - химический потенциал;

T - абсолютная температура (22.2.3);

k - постоянная Больцмана (22.2.5).

В отличие от распределения Ферми-Дирака (29.3.2.1, 29.3.2.2) в знаменателе стоит минус единица. Вследствие этого химический потенциал μ для бозонов не может быть положительным. Иначе при E_i < μ (если бы μ> 0!) показатель экспоненты в знаменателе стал бы отрицательным, экспонента стала бы меньше единицы и некоторые из чисел заполнения n_i стали бы отрицательными, что невозможно.

Если полное число частиц в системе не фиксировано, как, например, для фотонов при тепловом излучении (26.2), то химический потенциал μ равен нулю.

При фиксированном числе частиц величину μ определяют из условия нормировки, как и в случае распределения Ферми-Дирака (29.3.2.3).

29.6.2. Фотонный газ

При обычных, не лазерных, интенсивностях фотоны можно считать невзаимодействующими между собой бозонами, поэтому тепловое излучение, находящееся в равновесии со стенками излучающей полости можно рассматривать как идеальный фотонный газ.

Как было отмечено выше, химический потенциал для системы фотонов μ = 0. Энергия фотона  (26.1.3, 26.1.4), следовательно распределение Бозе-Эйнштейна для фотонов имеет следующий вид:

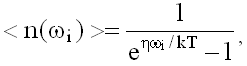
здесь <n(ω_i)> - среднее число фотонов с частотой ω_i. Частота ω_i  задает квантовое состояние фотона.

29.6.3. Вывод формулы Планка для u(ω, Т) - функции распределения плотности энергии в спектре излучения абсолютно черного тела

Пусть ΔE обозначает энергию фотонов, находящихся в объеме ΔV и имеющих частоты, лежащие в интервале Δω.

Тогда

имеет смысл функции распределения плотности энергии в спектре излучения абсолютно черного тела (спектральное распределение).

Пусть Z(ω_i) - число квантовых состояний фотонов в объеме ΔV и интервале частот от ω_i до ω_i + Δω.

Тогда

так как произведение  дает среднюю энергию фотонов частоты ω_i, т.е. среднюю энергию в одном квантовом состоянии. Функция известна (29.6.2), поэтому задача состоит в нахождении числа квантовых состояний Z(ω_i).

Подсчет числа квантовых состояний Z делается аналогично (29.2.2) и (29.3), т.е.:

здесь двойка учитывает две возможные поляризации фотонов. Фазовый объем.

где 4πp²Δp - объем сферического слоя в пространстве импульсов.

Импульс фотона

значит

Тогда

Так как частоты ω_i меняются квазинепрерывно, то мы опустили индекс i, нумерующий квантовые состояния.

Подставляя в формулу для ΔE полученное выражение Z(ω) и функцию распределения Бозе-Эйнштейна для фотонов (29.6.2), получим:

Используя это выражение, получим формулу Планка для функции распределения плотности энергии в спектре излучения абсолютно черного тела:

Из нее, как показано в (26.2.4.2) и (26.2.4.3), следует формула для спектральной плотности энергетической светимости абсолютно черного тела.

Сибирская государственная геодезическая академия (СГГА), 2006.