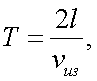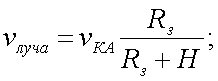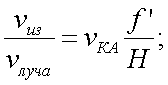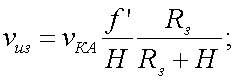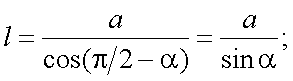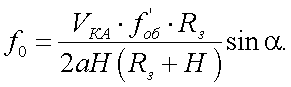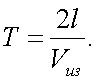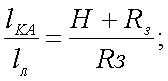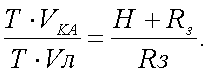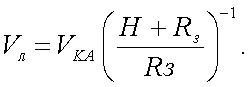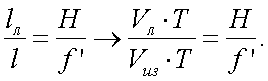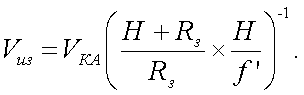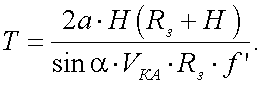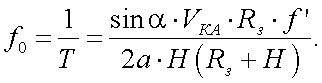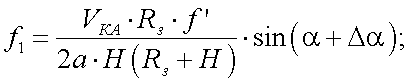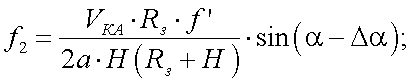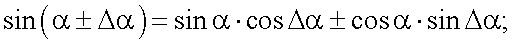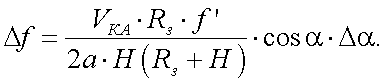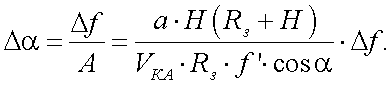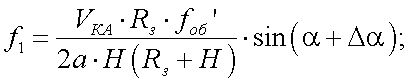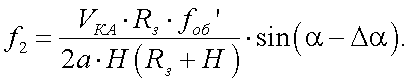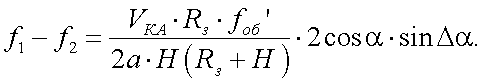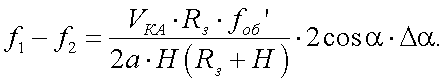Этот способ основан на модуляции лучистого потока, создающего изображение поверхности Земли. Принцип действия устройства, реализующего указанный способ, заключается в следующем. В состав прибора входят два оптико-электронных датчика. В фокальной плоскости каждого из них устанавливается частотный растр в виде чередующихся прозрачных и непрозрачных полос одинаковой ширины. Лучистый поток с выхода растров поступает на фотоэлектрические приемники излучения (рис. 20.1).
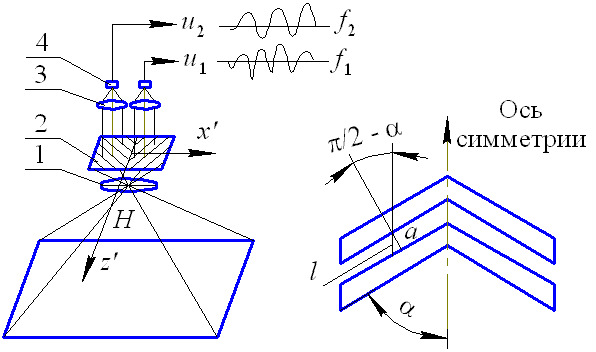
Рис. 20.1. Функциональная схема ОЭП курсовой ориентации, основанной на использовании частотных растров
Частота модуляции потока излучения может быть определена, исходя из параметров растров. Если ось симметрии частотных растров совпадает с вектором относительной скорости, то частота модуляции обоих растров одинакова и равна:
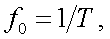 |
(20.1) |
где T – период перемещения изображения в плоскости решетки. Период T связан с длиной l изображения в пределах одной щели растра соотношением:
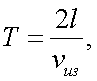 |
(20.2) |
где vиз – скорость перемещения изображения.
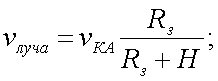
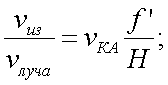
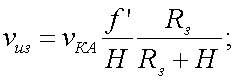 |
(20.3) |
где vКА – относительная скорость КА;
Rз – радиус Земли;
Н – высота полета КА;
f ' – фокусное расстояние объектива прибора.
Если угол наклона щелей растра к оси симметрии α, то l будет
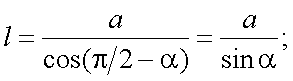 |
(20.4) |
где а – ширина щели.
С учетом (20.2), (20.3), (20.4) из (20.1) имеем:
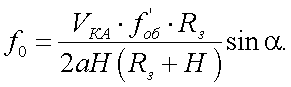 |
(20.5) |
Если ось КА отклонилась от вектора Vотн. на угол Δα, то из-за изменения l будут отличаться и частоты в левом и правом каналах от f0 и могут быть определены из выражений, приведенных ниже (рис. 20.2).
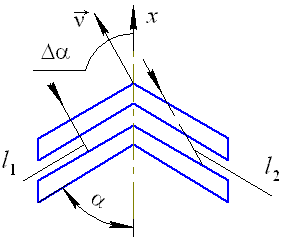
Рис. 20.2. К выводу угла рассогласования Δα в функции разности частот Δf
Рассмотрим подробно вывод функциональной связи угла рассогласования Δα с разностной частотой Δf. Для этого рассмотрим рис. 20.3, где помимо обозначений, приведенных выше, приняты следующие обозначения:
З – поверхность Земли;
lka – путь, пройденный космическим аппаратом в космосе за период времени Т;
lл – путь визирного луча оптико-электронного датчика на поверхности Земли при движении КА.
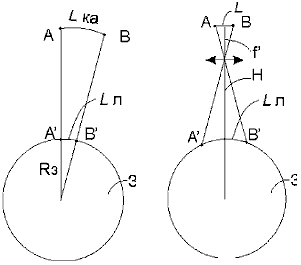
Рис. 20.3. К выводу соотношения (20.12)
Если принять во внимание, что пространственный период растра равен 2l, то справедлива формула:
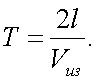 |
(20.6) |
На основании геометрии рис. 20.3, а имеем
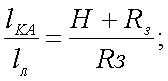 |
(20.7) |
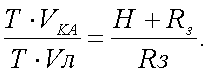 |
(20.8) |
Тогда, с использованием выражения (20.8), имеем:
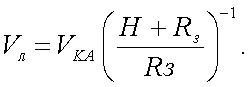 |
(20.9) |
Из геометрии рис. 20.3,б можно записать
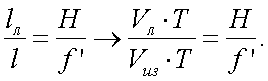 |
(20.10) |
Далее, воспользовавшись формулами (20.9) и (20.10), имеем:
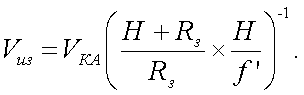 |
(20.11) |
На основании топологии растра, длина отрезка l равна
 |
(20.12) |
Подставив формулу (20.12) в выражение (20.6) и принимая во внимание формулу (20.11), получаем соотношение для периода Т перемещения изображения в плоскости частотного растра
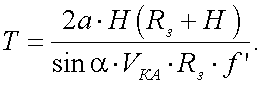 |
(20.13) |
В свою очередь, электрическая частота f0 равна:
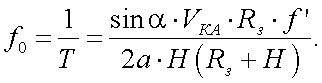 |
(20.14) |
В формулах (20.13) и (20.14) угол α – это угол наклона щелей растра к его оси симметрии.
Если продольная ось КА отклонилась на угол Δα от вектора относительной скорости, то из-за изменения длины пути l частоты в левом и правом каналах будут отличаться от f0 и могут определяться из выражений:
 |
(20.15) |
при этом
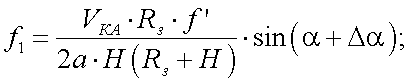 |
(20.16) |
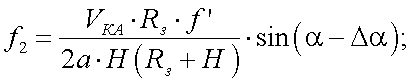 |
(20.17) |
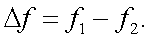
Воспользуемся тригонометрическим соотношением:
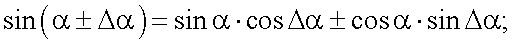

Тогда разностная частота принимает вид:
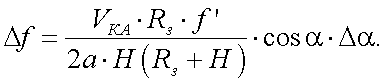 |
(20.18) |
Так как все параметры эксперимента в формуле (20.18) известны, то справедливы соотношения:
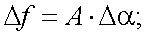 |
(20.19) |
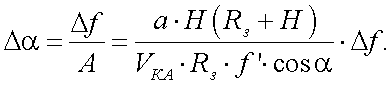
Определим значения частот f1 и f2:
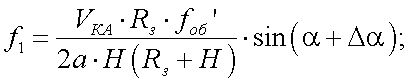
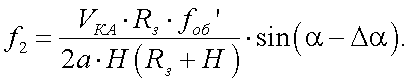
Тогда разностная частота имеет вид:
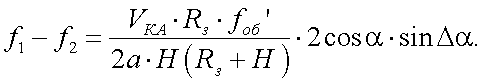
При sinΔα ≈ Δα имеем:
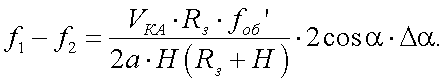 |
(20.20) |