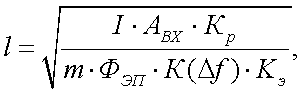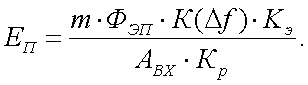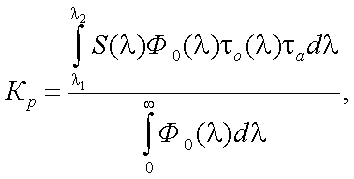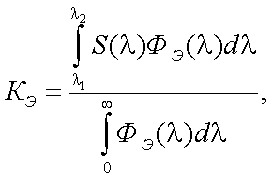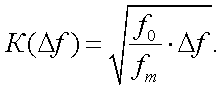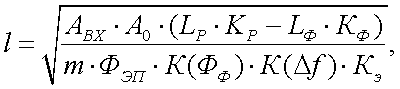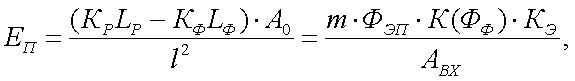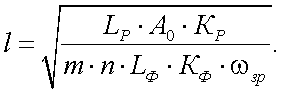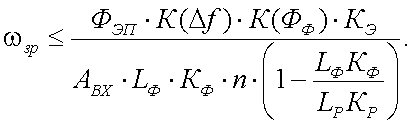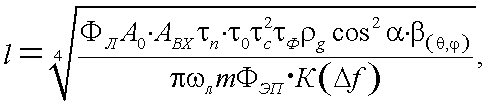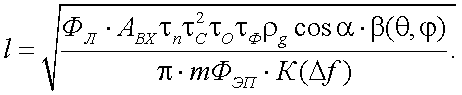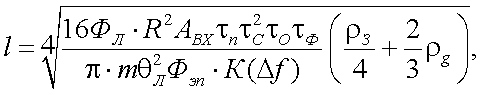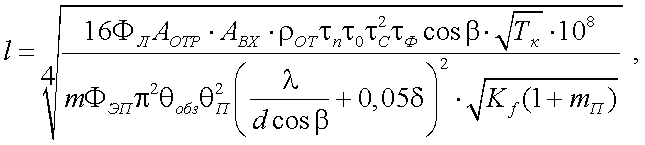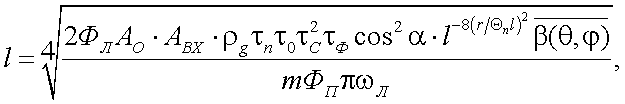43.1. Дальность действия пассивных ОЭП обнаружения, наведения и самонаведения
Наиболее простые соотношения для расчета дальности действия и пороговой чувствительности пассивных ОЭП обнаружения и самонаведения получены в работе [13]. Так, для случая работы прибора при отсутствии фона, в этой работе приводятся следующие выражения для дальности l и пороговой освещенности ЕП на входном зрачке прибора:
 |
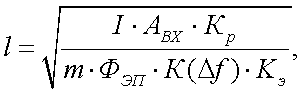(43.1) |
 |
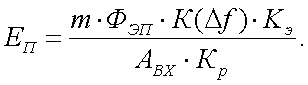(43.2) |
Здесь приняты следующие обозначения:
I – интегральная сила излучения объекта в направлении прибора;
КР – коэффициент использования приемником излучения объекта с учетом ослабления средой (атмосферой) и деталями оптической системы;
КЭ – коэффициент использования приемником излучения эталонного источника;
m – отношение «сигнал/шум»;
ФЭП – пороговый поток приемника по излучению эталонного источника на единицу полосы частот;
AВХ – площадь входного зрачка объектива ОЭП;
К(∆f) – коэффициент, учитывающий изменение частоты модуляции и ширины полосы усилителя с эталонными условиями измерения.
При использовании выражений (43.1) и (43.2) следует принять во внимание, что параметры КP, КЭ рассчитываются по формулам:
 |
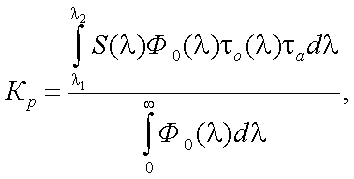(43.3) |
 |
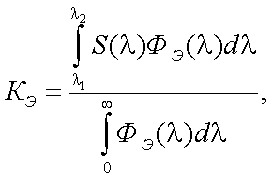(43.4) |
где S(λ) – относительная спектральная чувствительность приемника излучения;
λ1, λ2 – длина волн левой и правой границы спектральной чувствительности приемника излучения;
ФO(λ) – спектральный поток излучения объекта;
ФЭ(λ) – спектральный поток излучения эталонного источника;
To(λ), τa(λ) – спектральный коэффициент пропускания соответственно оптической системы ОЭП и слоя атмосферы между объектом наблюдения и прибором.
Коэффициент К(∆f ) равняется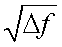 
в случае, когда ширина полосы частот усилителя мала по сравнению с частотой модуляции fM. В тех случаях, когда fM отличается от эталонной частоты модуляции f0 потока излучения, то указанный коэффициент берут в виде [13]:
 |
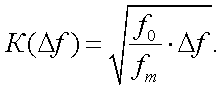(43.5) |
В случае наблюдения объекта на равномерно излучающем фоне, то в работе [13] получены следующие выражения для дальности l и пороговой освещенности Еn
 |
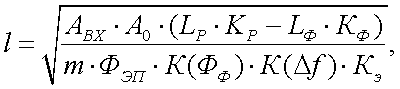(43.6) |
 |
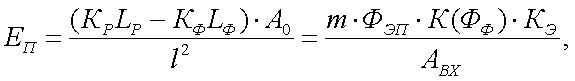(43.7) |
где Lp, LФ – интегральная яркость излучения соответственно объекта и фона;
КФ – коэффициент использования приемником излучения фона;
К(ФФ) – коэффициент, характеризующий ухудшение чувствительности приемника излучения при засветке фоном;
А0 – площадь проекции объекта на направление наблюдения.
Интересной ситуацией является наблюдение объекта на неравномерно излучающем фоне. В работе [13], для этого случая, получено следующее выражение для дальности действия l:
 |
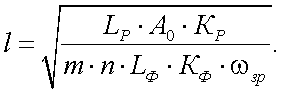(43.8) |
Здесь:
n – глубина модуляции потока излучения от фона;
ω3P – телесный угол зрения оптической системы ОЭП.
Из этой формулы видно, что дальность действия ОЭП при их работе на неравномерном фоне в отличие от дальности при работе на равномерном фоне не зависит от площади входного зрачка АВХ.
При необходимости обеспечения максимальной дальности действия, ограничиваемой только параметрами приемника излучения, величину переменной составляющей излучения фона стремятся уменьшить до такой степени, чтобы она стала меньше порогового потока прибора. Как видно из формулы (43.6), этого можно добиться только уменьшением размеров мгновенного поля зрения (если фон заполняет все поле зрения). Предельно допустимую величину мгновенного поля зрения можно найти при совместном решении зависимостей (43.6) и (43.8), причем формула (43.6) определяет максимальную дальность действия, а (43.8) – минимальную.
Возведя в квадрат правые части указанных зависимостей и приравнивая их, предельно допустимую величину мгновенного поля зрения находим в виде:
 |
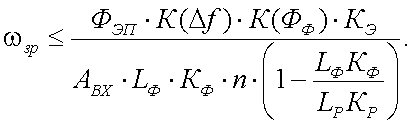(43.9) |
43.2. Дальность действия активных ОЭП лазерной локации при равномерном распределении энергии в сечении пучка лазера
Приемлемые для теории и практики соотношения для расчета дальности действия активных ОЭП с лазерами получены в работе [13]. Так, применительно к активным ОЭП с лазерами, для которых имеет место равномерное распределение энергии в сечении пучка лазера, получено следующее выражение для дальности действия l:
 |
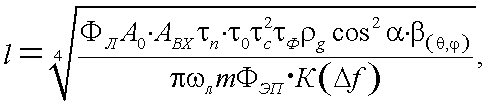(43.10) |
где: ФЛ – мощность лазера;
ωЛ – телесный угол расходимости лазерного излучения на выходе передающей части активного ОЭП;
τn, τ0 – коэффициент пропускания, соответственно, передающей и приемной части прибора;
τc, τФ – коэффициенты пропускания, соответственно, слоя атмосферы между объектом и прибором и фильтра;
ρg – диффузный коэффициент отражения поверхности лоцируемого объекта.
β11(Θ, φ) = β(Θ, φ) – приведенный коэффициент габаритной яркости поверхности объекта. Значение этого коэффициента для различных форм объектов приведены в работах [8, 9, 17, 20];
α – угол между нормалью к поверхности объекта и оптической осью приемной части прибора (в работе [13] при выводе выражения (43.10) считалось, что оптические оси передающей и приемной части прибора совпадают);
А0 – площадь поверхности объекта, которая полностью освещается лучами лазера передающей части прибора.
В тех случаях, когда угол ωЛне превышает угловых размеров объекта, то отраженное излучение от объекта будет поступать на приемник излучения не со всей поверхности объекта, а только с его облучаемой части. Для этого случая, дальность действия l принимает другой вид [13]:
 |
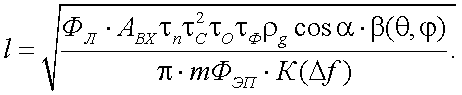(43.11) |
Если поверхность объекта не является плоской, а, например, сферической, то в этой же работе [13], для случая, когда ωЛ превышает угловые размеры лоцируемого объекта и его покрытие имеет зеркальную и диффузионную составляющие отражения, получена следующая формула для дальности действия l:
 |
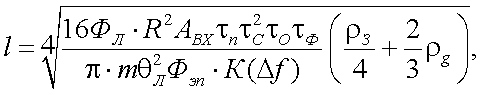(43.12) |
здесь ρЗ – коэффициент зеркального отражения материала покрытия объекта;
ΘЛ – плоский угол расходимости лазерного пучка передающей части прибора;
R – радиус сферы.
Иногда с целью увеличения дальности действия приборов на объектах устанавливают специальные уголковые отражатели (катафоты). При их использовании дальность действия рассчитывается по формуле [13]:
 |
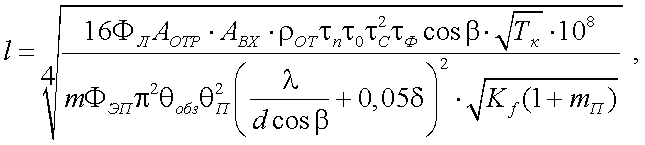(43.13) |
здесь λ – длина волн лазера;
d – линейный размер входной грани одного уголкового отражателя;
АОТР – площадь отражающей поверхности всего блока уголковых отражателей;
ρОТ – коэффициент отражения катафота;
δ – расходимость отраженного пучка из-за неточности изготовления отражателя;
Кf – коэффициент, учитывающий форму зондирующего импульса;
Тк – длительность зондирующего импульса;
mП – коэффициент перекрытия пространства при обзоре.
По формуле (43.13) можно рассчитать дальность действия оптико-электронного локатора по объекту, снабженному блоком угловых отражателей. Величины, входящие в эту формулу, подставляют в следующих размерностях:
ФЛ – Вт; АОТР и АВХ – м2; ФЭП – Вт /Гц1/2;
K(Δf) – Гц1/2; ΘП – рад; λ – мкм; d – см;
δ – угловые секунды; ρот, τn, τc, τo, τф, m – безразмерные.
43.3. Дальность действия активных ОЭП с гауссовым распределением энергии в сечении пучка лазера
Помимо работы [13], вопросы энергетического расчета ОЭП с лазерами рассмотрены в работе [16]. Так, когда в сечении пучка лазера передающей части активного оптико-электронного прибора (АОЭП) имеется гауссово распределение энергии, то в этой работе получено следующее выражение для дальности действия АОЭП:
 |
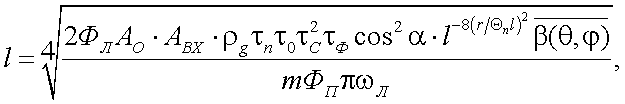(43.14) |
здесь ФП – пороговый поток приемника излучения;
r – расстояние между центром объекта и оптической осью передающей части приборов в пространстве предметов.
Значения коэффициента габаритной яркости
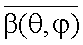для объектов в виде диффузных диска, сферы и цилиндра приведены в работе [20]. Для анализа влияния формы поверхности объекта и состояния поляризации как освещающего объект излучения, так и отраженного (излучаемого) его поверхностью, в работе [24] дана методика уточненного энергетического расчета активных и пассивных ОЭП, в том числе, и оптико-электронных координаторов.
