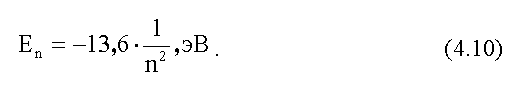ЛЕКЦИЯ N 4

Боровская теория атома водорода
Спектр излучения атома водорода в теории Бора

 

§ 1. Боровская теория атома водорода

Атом водорода - простейший из всех атомов. Его ядро - элементарная частица протон. Масса протона в 1836 раз больше массы электрона, вследствие этого ядро в первом приближении можно считать неподвижным и рассматривать только движение электрона (см. рис. 4.1).

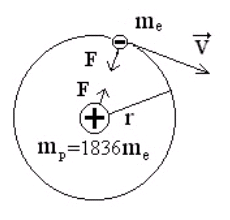
Рис. 4.1.

Заряд протона равен e, он положительный и равен по абсолютной величине заряду электрона, поэтому между ядром и электроном действует кулоновская сила притяжения.

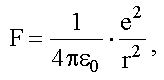
здесь e = 1,6·10^-19 Кл - элементарный заряд.

По второму закону Ньютона (см. Ч. 1, (4.4)):

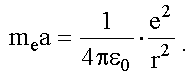
При равномерном движении по окружности радиуса r нормальное ускорение электрона:

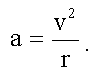
После подстановки этого выражения во второй закон Ньютона получим уравнение движения электрона:

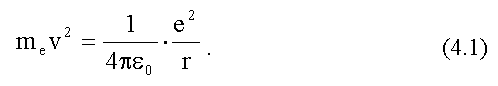
Из этого уравнения не следует никаких ограничений на r - радиус орбиты электрона. Так появилась проблема размера атома:  классическая механика позволяла     атому    иметь    любой     размер, опыт же показывал, что величина R ~ 10^-10 м.

 Кроме этой проблемы здесь существовала упомянутая в лекции N 1 (см. конец §1) проблема стабильности атома: в классической теории ускоренно движущийся электрон должен непрерывно излучать энергию, в результате чего электрон в атоме очень скоро, за время ~10^-8 с упадет на ядро.

Проблемы эти были разрешены Н. Бором на основе двух сформулированных им постулатов, дополненных условием стационарности состояния атома. Вот эти постулаты.

Первый постулат Бора:

Существуют стационарные состояния атома, находясь в которых он не излучает электромагнитных волн.

Стационарные состояния соответствуют дискретному ряду дозволенных значений полной энергии E_n (n = 1,2,3,...) (в квантовой физике мы будем обозначать полную энергию буквой Е, потенциальную - буквой U). Изменение энергии связано с квантовым (скачкообразным) переходом атома из одного стационарного состояния в другое.

Условие стационарности состояния атома - квантование момента импульса электрона L.

При движении электрона по круговой орбите радиуса r_n (n = 1,2,3,...)  его момент импульса  L_n = m_evr_n должен быть кратен постоянной Планка, деленной на 2π, т.е.

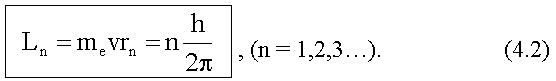
Здесь m_e - масса электрона; v - его скорость. Число n называют главным квантовым числом.

Так как 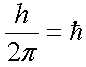 , то с учетом этого обозначения условие квантования орбит будет иметь следующий вид:

 

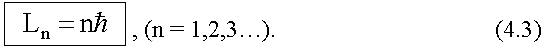
Второй постулат Бора:

Излучение испускается или поглощается в виде квантов энергии 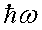при переходе электрона из одного стационарного состояния в другое. Энергия кванта (фотона) равна разности энергий стационарных состояний атома, между которыми происходит переход:

Здесь   E_n - энергия   стационарного   состояния   атома  до перехода электрона;

         E_m - энергия  стационарного  состояния  после  квантового  перехода  электрона. При E_n > E_m фотон с энергией 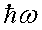 излучается, при E_n < E_m атом поглощает фотон .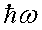

Как мы видим, постоянная Планка появляется у Бора дважды: первый раз она определяет стационарные состояния, второй - частоту излучения (или поглощения) при переходе атома из одного стационарного состояния в другое.

Применим условие стационарности состояния атома (4.2.). С помощью этого условия исключим из уравнения (4.1) скорость v. В результате для радиусов стационарных орбит r_n получим:

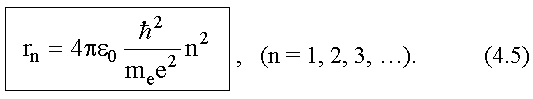
Радиус первой орбиты (n = 1)  называется первым боровским радиусом, его обозначают r₀. Численное значение первого боровского радиуса:

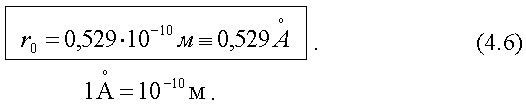
Полная энергия E атома водорода в нашей модели равна сумме кинетической энергии (m_ev²_max)/2 и отрицательной потенциальной энергии взаимодействия электрона с ядром: (-e²)/(4πε₀r), т.е.

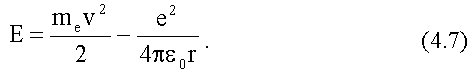
Из уравнения движения электрона (4.1) заменим в (4.7) mv²/2  на e²/(8πε₀r), тогда полная энергия атома водорода

 

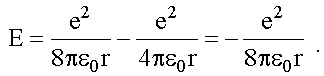
Подставив сюда выражение для r_n из (4.5), получим E_n - энергию стационарного состояния атома водорода, зависящую от главного квантового числа n:

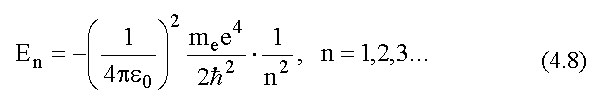
Состояние атома водорода при главном квантовом числе n = 1 называется основным состоянием. Численное значение энергии основного состояния атома водорода:

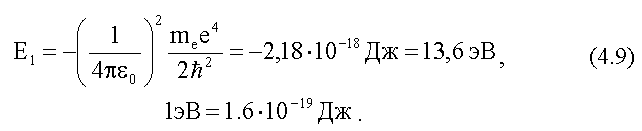
С учетом значения E₁ энергия стационарного состояния E_n  имеет простой вид: