
 Следующая страница !
Следующая страница !
Предыдущая страница ! |
Содержание |  Следующая страница ! Следующая страница !
|
3.1. Материальная точка, система материальных
точек, абсолютно твердое тело - простейшие физические модели
3.1.1. Материальная точка
Материальная точка - это одна из простейших физических моделей
(1.3).
 |  |
 |
 |  |
| реальный мир | исследователь | модельный мир |
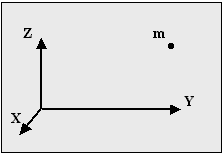
Тело из реального мира (см. рис.) иногда можно без ущерба для решаемой задачи заменить точкой в модельном мире, сохранив из всех многообразных свойств этого тела лишь два: положение в пространстве и массу. Эти две характеристики легко описать языком физики (1.4). Массу задают числом. Положение - координатами в выбранной системе координат (3.4.1).
Традиционное определение материальной точки: это тело,
размерами которого можно пренебречь при описании его движения. Здесь вместе
присутствуют понятия, описывающие и реальный мир, и модельный мир.
3.1.2. Система материальных точек
Если решается задача о движении нескольких материальных тел и каждое из них можно в
условии данной задачи заменить материальной точкой, то моделью этой системы
(1.3) будет система материальных точек.
Пример:
 |  |
 |
 |  |
| реальный мир | исследователь | модельный мир |
3.1.3. Абсолютно твердое тело
Существуют такие задачи, в которых размерами тела нельзя
пренебречь, но, в то же время, можно не учитывать изменение со временем размеров, формы тела.
При решении таких задач используют модель - абсолютно твердое тело, т.е. реальное тело
заменяют таким, у которого размеры и форма не меняются.
 |  |
 |
 |  |
| реальный мир | исследователь | модельный мир |
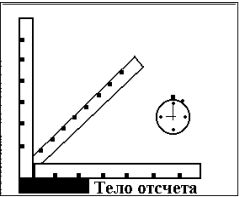
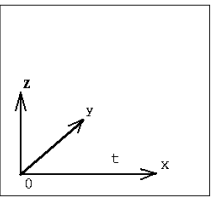
В реальном трехмерном мире система отсчета - это набор масштабных стержней (или линеек) и часы, расположенные в разных местах этих линеек. В модельном мире система отсчета превращается в трехмерную систему координат, положение которой связано с положением тела отсчета. В каждой точке пространства существует возможность определить время любого происшедшего в этой точке события.
3.4. Положение материальной точки в пространстве 3.4.1. Координаты точки
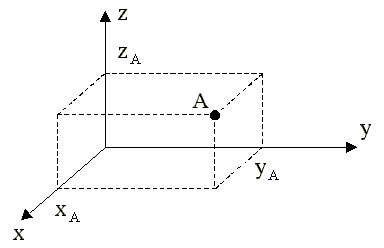
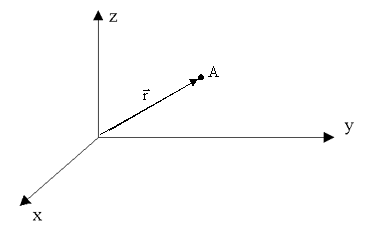
Первый способ задать положение материальной точки - это задать ее
координаты. Например, три числа xА, yА,
zА задают положение точки A в
декартовой системе координат. 3.4.2.1. Компоненты радиус-вектора На плоскости:
- x, y, z - компоненты радиуса - вектора. Очевидно, они же являются
координатами материальной точки.
3.4.2.2. Модуль радиус-вектора
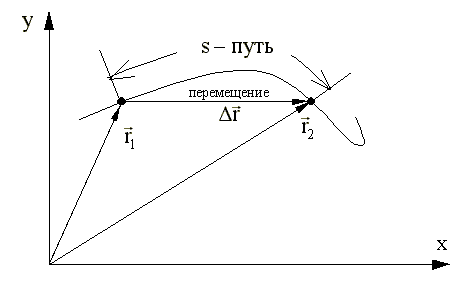
3.6. Путь - длина отрезка траектории
(3.5) .
3.7. Перемещение - вектор, проведенный из начального положения
(3.4.1), (3.4.2) материальной
точки (3.1.1) в ее конечное положение.
Так как
3.4.2. Радиус-вектор r - это вектор, проведенный из начала координат
(3.3)
в какую-либо точку пространства.
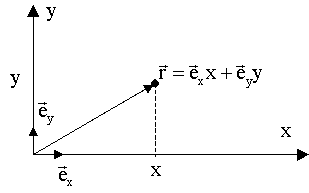
В трехмерном пространстве:
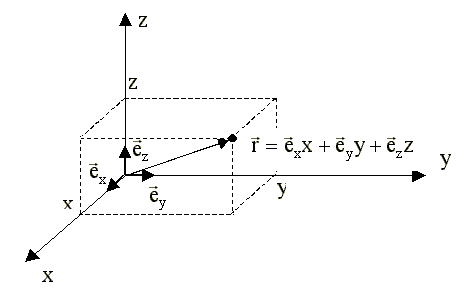
- 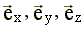 - единичные векторы или орты,
направленные по осям x, y, z соответственно;
- единичные векторы или орты,
направленные по осям x, y, z соответственно;
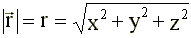 - по теореме Пифагора.
- по теореме Пифагора.
3.5. Траектория - это линия, описываемая материальной точкой
при ее движении.
3.8. Скорость - это производная радиуса - вектора
по времени.
 либо, применяя другое обозначение производной
по времени,
либо, применяя другое обозначение производной
по времени, 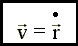
3.8.1. Скорость направлена по касательной к
траектории
 , то направление вектора
, то направление вектора
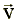 совпадает с предельным направлением вектора
совпадает с предельным направлением вектора
 . На рис. а), б), в) показаны этапы предельного перехода для
плоского движения (для простоты иллюстрации):
. На рис. а), б), в) показаны этапы предельного перехода для
плоского движения (для простоты иллюстрации):
| а) |

 к
к
 ,
,  по направлению приближается к касательной.
по направлению приближается к касательной.
| б) |

Как известно из геометрии, касательная есть предельное положение секущей.
| в) |

3.8.2. Компоненты скорости
На следующем рисунке изображен вектор скорости
Так как С другой стороны: откуда
т.е.
компоненты скорости равны производным соответствующих координат по времени.
3.8.3. Модуль скорости - производная пути по
времени.
3.9. Вычисление пройденного пути
Для равномерного движения 3.10. Ускорение - это производная
скорости по времени.
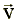 материальной точки M, движущейся по плоскости x, y:
материальной точки M, движущейся по плоскости x, y:

vx, vy - компоненты скорости, т.е. проекции вектора
на координатные оси.
 .
.
 ,
,
 , так же и
, так же и  ,
,
 .
. .
.
 ,
,
 - весь путь,
- весь путь,  - весь отрезок
времени,
- весь отрезок
времени,  - const.
- const.

 .
.
В пределе:
 ,
, или
или


Ускорение - это скорость изменения скорости.
Предыдущая страница ! |
Содержание |  Следующая страница ! Следующая страница !
|