КОЛЕБАНИЯ 14. ФИЗИКА КОЛЕБАНИЙ

14.1. Понятие о колебательных процессах

Колебаниями называются движения или процессы, обладающие той или иной повторяемостью во времени.

Примеры колебаний:

1. колебание величины заряда на обкладках конденсатора в колебательном контуре;

2. колебание грузика, закрепленного на пружине;

3. колебание маятника.

   14.1.1. Гармонические колебания

Гармонические колебания - это такие колебания, при которых колеблющаяся величина x изменяется со временем по закону синуса, либо косинуса:

,

или

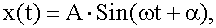
где A - амплитуда;
     ω - круговая частота;
     α - начальная фаза;
( ωt + α ) - фаза.

14.1.1.1. Фаза колебания

Фаза колебания - это аргумент гармонической функции: ( ωt + α ). Начальная фаза α - это значение фазы в начальный момент времени, т.е. при t = 0.

14.1.1.2. Амплитуда колебания

Амплитуда колебания A - это наибольшее значение колеблющейся величины.

14.1.1.3. Круговая или циклическая частота ω

При изменении аргумента косинуса, либо синуса на 2π эти функции возвращаются к прежнему значению. Найдем промежуток времени T, в течение которого фаза гармонической функции изменяется на 2π .

ω(t + T) + α = ωt + α + 2π,

или

ωT = 2π. .

Время T одного полного колебания называется периодом колебания. Частотой ν называют величину, обратную периоду

.

Единица измерения частоты - герц (Гц), 1 Гц = 1 с^-1.

Так как

,

то

.

Круговая, или циклическая частоты ω в 2π раз больше частоты колебаний ν. Круговая частота - это скорость изменения фазы со временем. Действительно:

.

14.1.1.4. График гармонического колебания

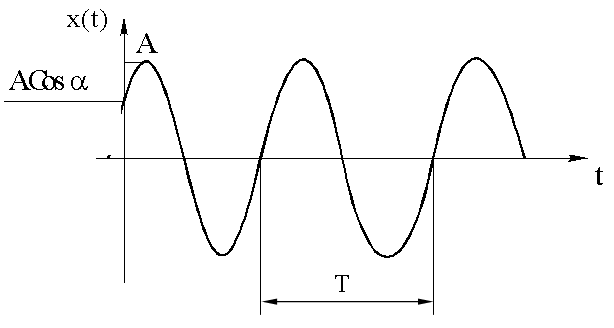
14.2 Дифференциальное уравнение гармонических колебаний

14.2.1 Колеблющиеся системы

Рассмотрим колебания в трех системах:

а) колебания заряда в колебательном контуре L,C;

б) колебания грузика, прикрепленного к пружине;

в) колебание физического маятника - любого тела, совершающего колебания вокруг горизонтальной оси, не проходящей через его центр тяжести.

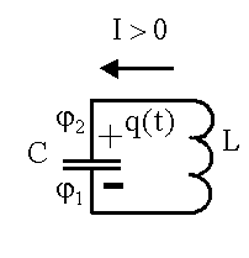
14.2.2 Колеблющиеся величины
q - заряд	x - координата грузика	φ - угол отклонения
14.2.3. Уравнения движения
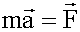
Закон Ома (10.7)	Второй закон Ньютона (4.6)	Уравнение динамики вращательного движения (7.3)
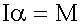
14.2.4. Применим закон движения, т.е. учтем особенности наших систем:
Используя другое обозначение производной получим после несложных преобразований:

Мы получили дифференциальные уравнения, описывающие движения наших систем. В первых двух случаях уравнения одинаковы по форме, в третьем случае второй член уравнения содержит не φ, а Sin φ . Если рассматривать только малые отклонения маятника от положения равновесия, то тогда, при φ << 1, Sin φ ≈ φ и мы имеем:

.

Введем обозначения:

,	,	,
,	,	.

14.2.5. Дифференциальное уравнение колебательного движения

Для всех трех рассмотренных случаев имеем одно и то же дифференциальное уравнение колебательного движения

.

14.2.6. Решение дифференциального уравнения

Решением дифференциального уравнения называется функция, обращающая это уравнение в тождество.

Нетрудно проверить прямой подстановкой, что в нашем случае решение имеет вид:

,

т.е. является гармонической функцией. Значит уравнение , это дифференциальное уравнение гармонических колебаний.

Сибирская государственная геодезическая академия (СГГА), 2003.