
 Следующая страница !
Следующая страница !
Предыдущая страница ! |
Содержание |  Следующая страница ! Следующая страница !
|
7.1. Работа при вращательном движении.
Момент силы

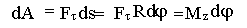 ,
,
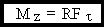 .
.
 - векторное произведение.
- векторное произведение.
7.2. Кинетическая энергия при вращательном
движении. Момент инерции
Моментом инерции материальной точки Ii называется величина:
7.2.1. Теорема Штейнера
7.2.2. Моменты инерции I0 для
некоторых тел
7.3. Уравнение динамики вращательного
движения  .
.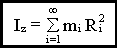 .
.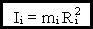 .
.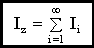 .
.
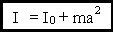 ,
,
I - момент инерции относительно оси O'О'.
Обруч:
 ,
,
где R - радиус обруча.
Диск:
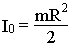 ,
,
где R - радиус диска.
Шар:
 ,
,
где R - радиус шара.
Стержень:
 ,
,
где l - длина стержня.
m - масса тела.
Из (5.5):
 .
.
Используем (7.1) и
(7.2):
 .
.
Используем (6.3):
 ,
, .
.
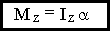 .
.
7.4. Момент импульса абсолютно твердого тела
Из (7.3):
 , или
, или
 .
.
 .
.
 .
.
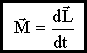 , сравнить с
(4.6)
, сравнить с
(4.6)
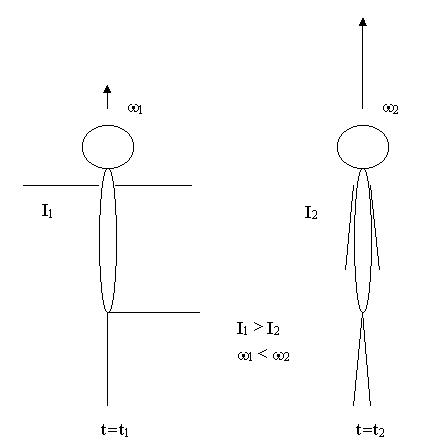
7.5. Закон сохранения момента импульса
Из (7.4):
 ,
,
 = 0, то:
= 0, то:
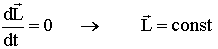 .
.
 , то величина
, то величина
 будет иметь одинаковые значения для любых интересующих нас моментов
времени, т. е.:
будет иметь одинаковые значения для любых интересующих нас моментов
времени, т. е.:
 ;
;
 .
.

Предыдущая страница ! |
Содержание |  Следующая страница ! Следующая страница !
|