
 Следующая страница !
Следующая страница !
Предыдущая страница ! |
Содержание |  Следующая страница ! Следующая страница !
|
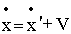 , , |
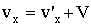 , , | |
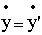 , , |
т.е., по (3.8): |
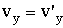 , , |
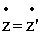 , , |
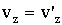 , , |
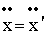 , , |
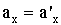 , , | |
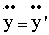 , , |
т.е., по (3.10): |
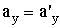 , , |
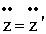 , , |
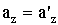 . . |
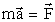 ,
,
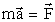 ,
,
8.3. Неудовлетворительность
механики Ньютона при больших скоростях
Рассмотрим с точки зрения преобразований Галилея движение
света.
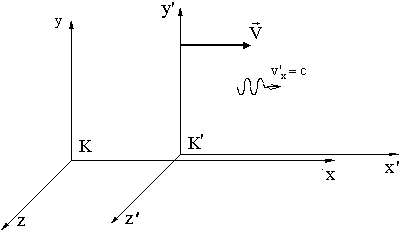
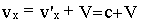
В 1895 г. французский математик, физик и философ А. Пуанкаре впервые выступил с новаторским предложением о невозможности никакими физическими опытами (не только механическими, как в принципе относительности Галилея) зарегистрировать абсолютное движение. В 1902 г. он же публикует в книге "Наука и гипотеза" утверждение об отсутствии абсолютного времени, т.е. t ≠ t'.
Законченная теория, позволяющая описывать движение частиц со скоростями v → с, была опубликована в 1905 г. в работах А. Пуанкаре и А. Эйнштейна.
8.4. Постулаты С.Т.О.
8.5. Преобразования Лоренца -
это уравнения, связывающие координаты и время некоторого
события (8.1) в двух инерциальных
системах отсчета. В отличие от преобразований Галилея преобразования Лоренца не должны
противоречить постулатам С.Т.О.: необнаружимости абсолютного движения и постоянству
скорости света. При скорости движения системы отсчета V<< c преобразования Лоренца должны
переходить в преобразования Галилея.
Механика больших скоростей, специальная теория относительности
(С.Т.О.),
базируется на двух исходных утверждениях, постулатах:
никакими физическими опытами нельзя установить, покоится ли данная система
отсчета, либо движется равномерно и прямолинейно.
Другая формулировка:
Все законы природы одинаково
формулируются для всех инерциальных систем отсчета
.
cкорость света в вакууме во всех инерциальных системах отсчета одинакова и
не зависит ни от движения источника, ни от движения приемника света .
| а) прямые | б) обратные | |
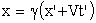 ; ; |
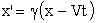 ; ; | |
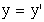 ; ; |
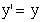 ; ; | |
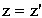 ; ; |
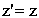 ; ; | |
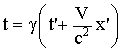 ; ; |
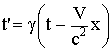 . . |
Релятивистская механика должна быть построена таким образом, чтобы уравнения движения не менялись при переходе из одной инерциальной системы отсчета в другую, т.е. были инвариантны относительно преобразований Лоренца.
8.6. Следствия из преобразований Лоренца
8.6.1. Одновременность событий в разных системах
отсчета
8.6.2. Промежуток времени между двумя событиями
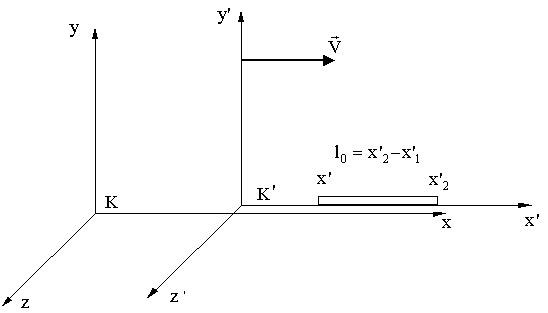
8.6.3. Длина тела в разных системах отсчета
Мы, в системе К, должны в один и тот же момент времени t (по чаcам системы
К) измерить координаты начала и конца стержня. Их разница и будет длиной движущегося стержня. Тогда:
8.6.4. Преобразование скоростей 8.7. Релятивистская динамика
В классической механике В релятивистской механике, где v → c,
8.7.2. Уравнение движения в релятивистской
механике такое же, как и в классической (4.6)
8.7.3. Релятивистское выражение для энергии
8.7.3.2. Кинетическая энергия
(энергия движения)
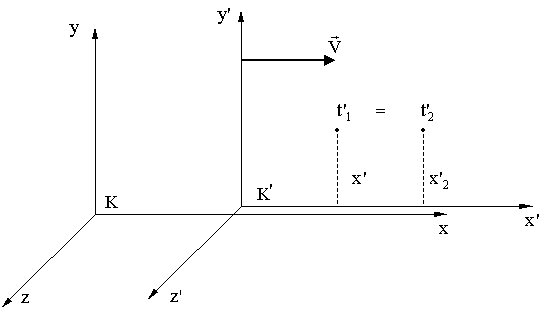
В системе K' одновременно
(в момент времени t'), нo в разных местах
(x'1 и, x'2) произошли два события.
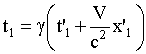 ,
,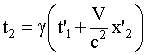 .
.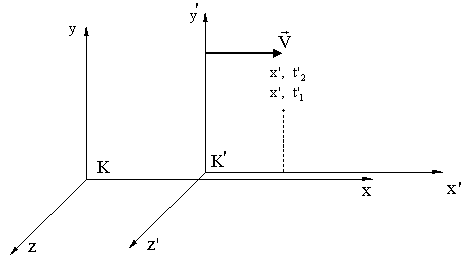
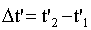
В системе К:
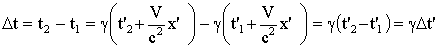 .
.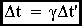 .
.
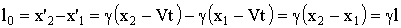 ,
,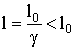 .
.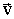 .
.
Система K' движется со скоростью 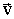 относительно K.
относительно K.
 .
.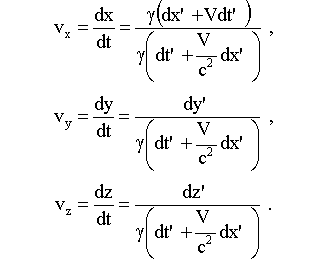
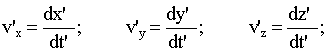 ;
;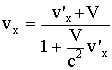 ;
;
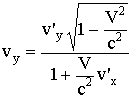 ;
;
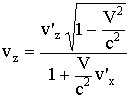 .
.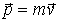 (4.5), при v << c.
(4.5), при v << c. 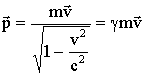 .
.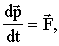 но
но
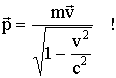
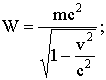
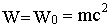
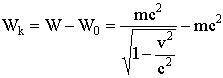 .
.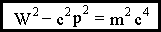 - inv, инвариант,
- inv, инвариант,
Предыдущая страница ! |
Содержание |  Следующая страница ! Следующая страница !
|