
 Следующая страница !
Следующая страница !
Предыдущая страница ! |
Содержание |  Следующая страница ! Следующая страница !
|
5.1. Механическая система - это совокупность тел,
выделенных нами для рассмотрения
5.1.1. Внутренние и внешние силы
 | Внутренние силы - силы, с которыми взаимодействуют тела системы между собой. |
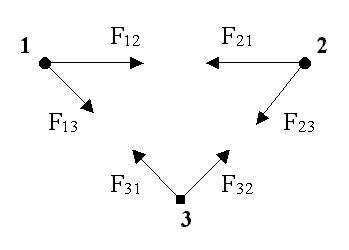
5.1.3. Импульс системы материальных
точек - это
векторная сумма импульсов всех материальных точек, входящих
в систему
5.2. Закон сохранения импульса
Импульс замкнутой системы сохраняется, т.е. не изменяется со временем.
На рисунке изображена замкнутая система, состоящая из трех тел.
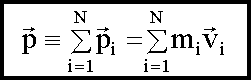 ,
(см. 4.5).
,
(см. 4.5).
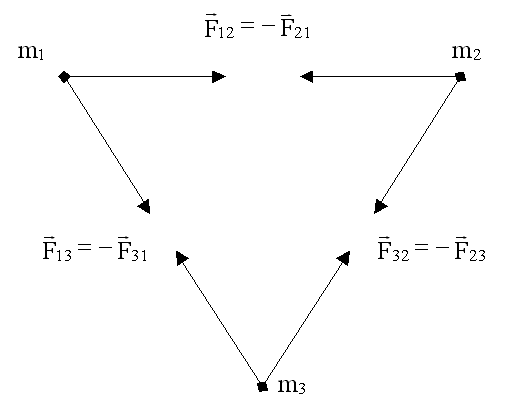

Сложим эти уравнения. Справа, по III закону
Ньютона (4.7), получим ноль. Слева - производную
по времени от полного импульса системы (5.1.3).


 |
рх = const, если Fx = 0, рy = const, если Fy = 0, рz = const, если Fz = 0. |
 |
рх = const, если Fx= 0, рy≠ const, если Fy ≠ 0, рz ≠ const, если Fz ≠ 0. |
5.3. Работа
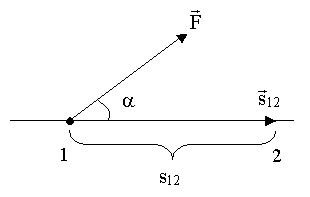
5.3.1. Работа постоянной силы
5.3.2. Элементарная работа
5.3.3.Работа переменной силы
5.3.4. Единица измерения работы
[A]=[F].[s]= H.м = джоуль, Дж 5.4. Мощность P
-
это скорость совершения работы,



т.е.
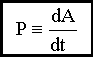
Используя (5.3.2) и
(3.8),

Здесь v - скорость материальной точки, к которой приложена сила
 .
.
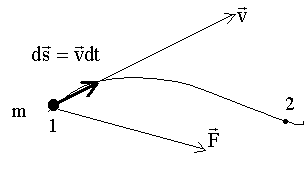 |
Применим II закон Ньютона для
материальной точки m, движущейся под действием результирующей силы
 : :
|
 - справа на
- справа на 
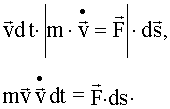 .
.

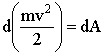 .
.


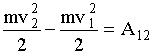

5.6. Консервативные и неконсервативные силы
Консервативные (conservativus - охранительный) -
такие силы, РАБОТА которых не зависит от траектории, а определяются только
начальным и конечным положением материальной точки.
Силы, не обладающие только что названным
свойством, называют неконсервативными.
Для того чтобы узнать, консервативна сила либо
нет, надо вычислить ее работу.
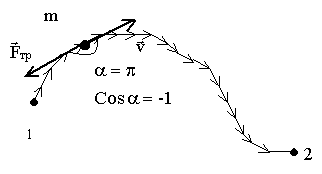 |
На рисунке изображен вид сверху на материальную точку m, движущуюся при наличии
силы трения из положения 1 в положение 2.
Сила трения всегда направлена против скорости  |

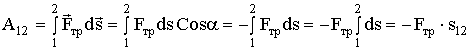 .
.
5.7. Потенциальная энергия может быть введена только для поля консервативных сил
Так как их работа не зависит от траектории, а только
от начального и конечного положений материальной точки, то эту работу можно записать в
виде разности двух чисел: одно - Wn1 - будет зависеть от начального положения
тела, второе - Wn2 - от конечного положения тела.
5.7.1. Некоторые конкретные
выражения для потенциальной энергии Wn(r)
5.8.Закон сохранения механической
энергии
5.8.1.Для одной материальной
точки, движущейся в поле консервативных сил, A12 = Wk2 - Wk1, A12 = Wn1 - Wn2. Wn1 - Wn2 = Wk2 - Wk1 Wk1 + Wn1 = Wk2 + Wn2. В поле консервативных сил сумма кинетической и потенциальной
энергии материальной точки остается постоянной, т.е. сохраняется.
 .
.
Wn1 - потенциальная энергия тела в положении 1;
Wn2 - в положении 2.
Для нахождения конкретного вида зависимости Wn(r)
необходимо вычислить работу 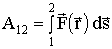 .
.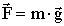 , используя
(5.6.1), получим: Wn = mgh.
, используя
(5.6.1), получим: Wn = mgh.
Если  - гравитационная сила,
то
- гравитационная сила,
то 
Если 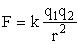 - кулоновская сила, то
- кулоновская сила, то
 .
.
Если 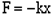 - сила упругости, то
- сила упругости, то
 .
.
из (5.5)  - полная энергия материальной
точки.
- полная энергия материальной
точки.
Полная энергия материальной точки в поле консервативных сил сохраняется.
Предыдущая страница ! |
Содержание |  Следующая страница ! Следующая страница !
|