 |
ВОЛНЫ16. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ |
| |
|||||
|
| |||||
 |
ВОЛНЫ16. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ |
| |
|||||
|
| |||||
16. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
Выпишем здесь еще раз систему уравнений Максвелла в дифференциальной форме вместе с материальными уравнениями (15.3):
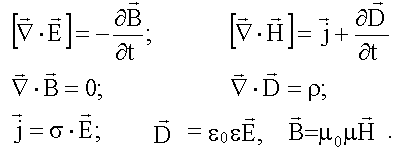
Применим систему уравнений Максвелла (13.4) к однородной ( ε = const, μ = const), нейтральной ( ρ = 0), непроводящей ( σ = 0) среде. Уравнения Максвелла примут следующий вид.
Первая пара:
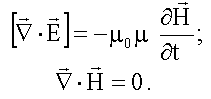
Вторая пара:
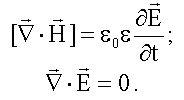
Наша задача - получить волновые уравнения для векторов
и
, решениями которых будут уравнения электромагнитной волны
(сравните с 15.3).
16.1. Система уравнений Максвелла для плоской электромагнитной волны
Зададим направление оси x перпендикулярно волновым поверхностям. Тогда:
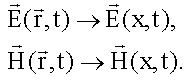
От координат x и z в плоской волне
и
не зависят. Как известно из математики:
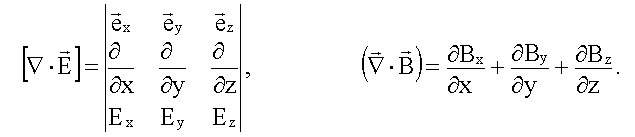
Учитывая, что
не зависит от y и z из первого уравнения первой пары:
,
получим три скалярных уравнения:
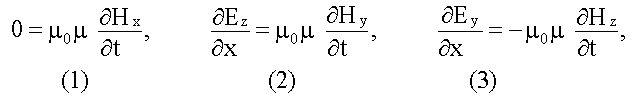
Второе уравнение первой пары дает:
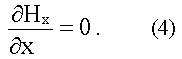
Аналогично, из второй пары уравнений Максвелла получим:
16.1.1. Поперечность электромагнитных волн
Уравнения (1) и (4), (5) и (8) утверждают, что Hx и Ex не зависят от времени и координаты x, т.е. являются однородными постоянными полями. Таким образом, переменное поле электромагнитной волны не имеет составляющей вдоль оси x, в направлении которой распространяется волна. Это значит, что электромагнитная волна поперечна, т.е. векторы
и
перпендикулярны направлению ее распространения.
16.1.2. Волновое уравнение
В уравнения (2) и (7) входят Ez и Hy, в уравнения (3) и (6) входят Ey и Hz. Таким образом, если первоначально было создано поле Ey, то оно породит Hz (3), которое создает Ey (6). Аналогично с Ez и Hy.
Для описания электромагнитной волны можно выбрать уравнения (2) и (7), либо уравнения (3) и (6), либо те и другие.
Получим волновое уравнение для уравнений (3) и (6):
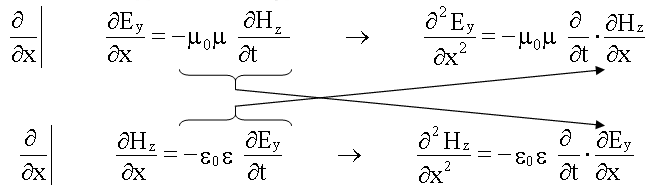
После указанных стрелками замен имеем два волновых уравнения:
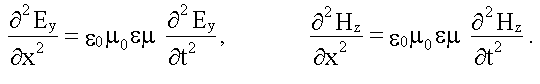
16.1.2.1. Фазовая скорость электромагнитной волны
Коэффициент при второй производной по времени, есть величина, обратная квадрату фазовой скорости волны (см. 15.3.2). Для электромагнитной волны фазовая скорость из волновых уравнений 16.1.2:

В вакууме ε = &mu = 1 и
.
Тогда:

Полученное значение фазовой скорости электромагнитной волны в вакууме равно скорости света в вакууме - с. С учетом этого:
16.1.2.2. Гармонические волны - простейшие решения волновых уравнений
Легко проверить, что
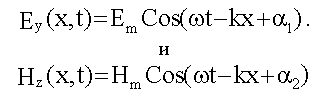
являются решениями волновых уравнений (16.1.2). Эти решения описывают электромагнитную волну, у которой вектор
направлен вдоль оси y, вектор
- вдоль оси z, волна распространяется вдоль оси x, таким образом, векторы
,
,
образуют правую тройку.
16.1.2.3. Связь между модулями векторов
и
электромагнитной волны и их фазами
Подставив решения (16.1.2.2.) в уравнения (3) и (6), получим из (3):
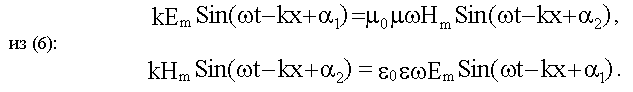
Из этих равенств следует:
1) Векторы
и
колеблются в одинаковой фазе.
;
2)
16.2. Пространственная структура электромагнитной волны
Для фиксированного момента времени t1 векторы
и
плоской гармонической электромагнитной волны могут быть изображены следующей диаграммой:
16.3. Плотность энергии электромагнитной волны
16.3.1. Вектор Пойнтинга - вектор плотности потока энергии электромагнитной волны
Из (15.4.4):
.
Для электромагнитной волны вектор плотности потока энергии обозначают буквой
.
Из (16.3):
.
Используя диаграмму (16.2) величине S можно придать векторный характер:
16.3.2. Интенсивность электромагнитной волны - это среднее по времени от модуля вектора Пойнтинга
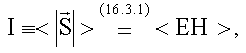
сравните с (15.4.5).
16.4. Изучение диполя16.4.1. Диполь
- это два разноименных точечных заряда, находящихся на некотором расстоянии друг от друга
(см. 9.13.1.1).
16.4.2. Электрическое и магнитное поле колеблющегося диполя
Пусть расстояние между зарядами диполя периодически изменяется с течением времени, т.е.
, диполь колеблется. Тогда
.
Электрическое и магнитное поле диполя будет переменным, диполь будет излучать электромагнитные волны.
Точный расчет на основе уравнений Максвелла показывает, что электрическое поле в этой волне, распространяющейся в вакууме:
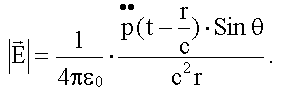
Направление векторов
и
изображено на рисунке. Угол θ - это угол между направлением дипольного момента
и направлением излучения.
16.4.2.1. Электрическое поле диполя, колеблющегося по гармоническому закону
Пусть
, тогда:
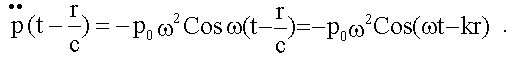
Для E из (16.4.2) имеем:
16.4.2.2. Интенсивность дипольного гармонического излучения
Из (16.3.2):
16.4.2.3. Диаграмма направленности излучения диполя
- это графическое изображение в полярной системе координат зависимости интенсивности излучения I, (16.4.2.2), от угла θ.
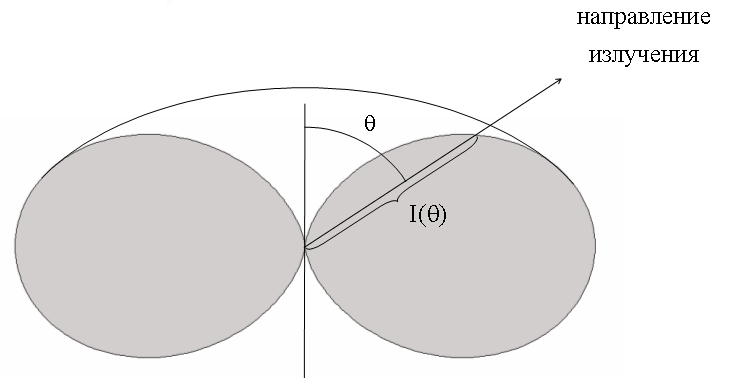
На рисунке дана половина пространственного изображения диаграммы направленности. Полная диаграмма похожа на бублик без дырки.
| Назад |
| Сибирская
государственная геодезическая академия (СГГА), 2003. |
|