КОЛЕБАНИЯ 14. ФИЗИКА КОЛЕБАНИЙ

Содержание Назад Далее

14.3. Сложение колебаний

14.3.1. Векторная диаграмма

Векторная диаграмма - это способ графического задания колебательного движения в виде вектора.

Аналитическое задание колебательного движения		Графическое задание колебательного движения

Вдоль горизонтальной оси откладывается колеблющаяся величина ξ (любой физической природы). Вектор , отложенный из точки 0 равен по модулю амплитуде колебания A и направлен под углом α , равным начальной фазе колебания, к оси ξ. Если привести этот вектор во вращение с угловой скоростью ω , равной циклической частоте колебаний, то проекция этого вектора на ось ξ дает значение колеблющейся величины в произвольный момент времени.

14.3.2. Сложение колебаний одинаковой частоты и одинакового направления

Пусть складывается два колебания:

строим векторные диаграммы и складываем векторы:

По теореме косинусов .

Так как

,

то

.

Очевидно (см. диаграмму), что начальная фаза результирующего колебания определяется соотношением:

.

14.3.3. Сложение колебаний близких частот

Пусть складывается два колебания с почти одинаковыми частотами, т.е.

,      .

Из тригонометрии:  . Применяя к нашему случаю, получим:

 

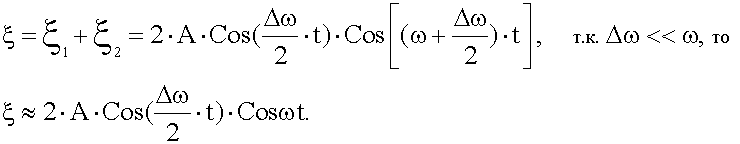
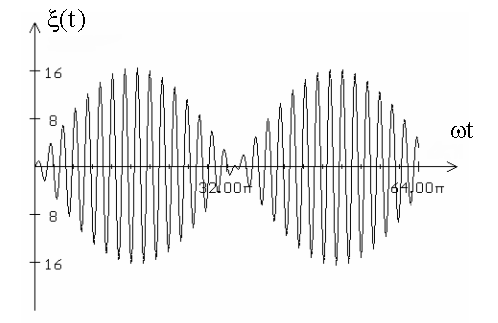
График результирующего колебания - график биений, т.е. почти гармонических колебаний частоты ω, амплитуда которых медленно меняется с частотой Δω .

Амплитуда из-за наличия знака модуля (амплитуда всегда > 0) частота с которой изменяется амплитуда, равна не Δω / 2 , а в два раза выше - Δω.

14.3.4. Сложение взаимно-перпендикулярных колебаний

Пусть маленькое тело колеблется на взаимно-перпендикулярных пружинках одинаковой жесткости. По какой траектории будет двигаться это тело?

Это уравнения траектории в параметрическом виде. Для получения явной зависимости между координатами x и y надо из уравнений исключить параметр t.

Из первого уравнения:

;           .

Из второго:

.

После подстановки:      .

Избавимся от корня:

.

- это уравнение эллипса.

Частные случаи:

1. 
   



2. 
   



3. 
   

14.4. Затухающие колебания

Рассмотрим колебания, происходящие в двух системах:

а) колебания заряда в колебательном контуре L,C, имеющем активное сопротивление R;

б) колебание грузика, прикрепленного к пружинке, учтем влияние трения на движение грузика.

14.4.1. Колеблющиеся системы

14.4.2. Законы движения
Закон Ома для неоднородного участка цепи (10.7):	Второй закон Ньютона (4.6):
14.4.3. Применение законов движения, с учетом особенности наших систем
Или, используя другое обозначение производной:
14.4.4. Введем обозначения:

 

14.4.5. Дифференциальное уравнение, описывающее затухающие колебания наших двух систем в этих обозначениях будет иметь один и тот же вид

.

14.4.6. Решение

Каким будет его решение? При    (отсутствие сопротивления, трения) оно должно переходить в    (см. 14.2).

Наличие затухания, потерь энергии, переход ее из электромагнитной или механической в тепловую приведет к уменьшению амплитуды колебаний с течением времени, станет другой, меньшей чем ω₀, и частота колебаний.

Предположим, что амплитуда убывает по экспоненциальному закону, т.е. A(t) = A₀·e^-βt(e=2,71828...),

тогда решение будем искать в виде:

.

14.4.7. Проверка

Выясним, при каких условиях эта функция будет решением, для этого найдем и подставим в дифференциальное уравнение.

Сгруппируем члены с косинусом и синусом, на A₀e^-βt сократим:

.

Для тождественного обращения левой части в ноль надо, что бы коэффициент при косинусе обращался в ноль (коэффициент при синусе обратился в ноль, т.к. мы "удачно" выбрали A(t) = A₀^-βt). Из этого требования следует выражение для - ω частоты затухающих колебаний.

14.4.8. Частота затухающих колебаний

.

14.4.9. Период затухающих колебаний

.

14.4.10. График затухающих колебаний

14.4.11. Переход к апериодическому движению

При увеличении коэффициента затухания β период затухающих колебаний (14.4.9) растет, при β → ω₀ период T → ∞ . При β > ω₀ периодическое решение у дифференциального уравнения затухающих колебаний отсутствует:

14.4.12. Логарифмический декремент затухания

,

подставим A(t) = A₀^-βt.

.

 

14.4.13. Время релаксации

Время релаксации - это время τ, за которое амплитуда уменьшилась в e=2,7... раз, т.е.  ,  тогда   .

.

Т.к.    - число колебаний за время , то:

.

14.4.14. Добротность

.

Сибирская государственная геодезическая академия (СГГА), 2003.