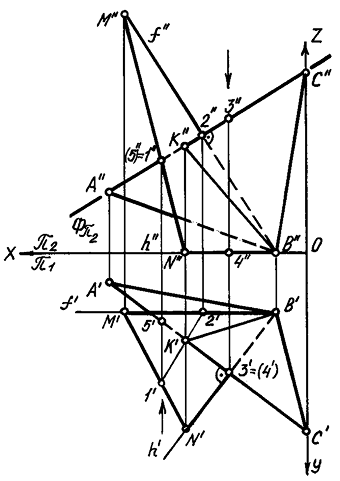
| |
| |
Задача
3 |
 |
|
Через
вершину В
ΔАВС
провести плоскость, перпендикулярную стороне AC.
Эту плоскость задать треугольником. Построить линию пересечения
двух треугольников и показать их видимость в проекциях.
|
Указания
к решению задачи: |
| 1) |
Плоскость
перпендикулярна прямой, если две пересекающиеся прямые на плоскости
перпендикулярны этой прямой. Поэтому прежде всего, через точку
В
надо провести две прямые, перпендикулярные стороне AC:
|
в соответствии с теоремой о проецировании прямого угла в качестве
двух прямых, перпендикулярных стороне AC,
надо использовать прямые частного положения - горизонтальную
и фронтальную;
на эпюре горизонтальная проекция горизонтальной
прямой h'
составит прямой угол с горизонтальной проекцией стороны А'C',
а фронтальная проекция фронтальной прямой f"
составит прямой угол с фронтальной проекцией стороны А"C".
|
| 2) |
Далее
следует образовать плоскость в виде треугольника, имеющего общую
точку В
с заданным ΔАВС,
а две другие точки надо взять произвольно на построенных двух
прямых:
|
на построенных прямых h
и f
надо взять произвольно две точки M
и N,
построить их проекции;
образованный Δ
MNB будет перпендикулярен Δ
АВС.
|
| 3) |
Затем
надо построить линию пересечения двух треугольников. Для этого
надо найти две точки, принадлежащие линии пересечения, т.к.
точка В
принадлежит обоим треугольникам, следовательно, она принадлежит
линии пересечения двух треугольников. Чтобы найти вторую точку,
принадлежащую линии пересечения, надо решить задачу на нахождение
точки встречи, например, стороны AC
ΔАВС
с плоскостью второго треугольника:
|
на эпюре для нахождения точки встречи
через фронтальную проекцию А"C"
надо провести вспомогательную фронтально проецирующую плоскость
ФП2;
затем нужно построить линию пересечения (1-2)
плоскости Δ
MNB с этой фронтально проецирующей плоскостью;
горизонтальная
проекция точки встречи К'
стороны АC
с плоскостью Δ
MNB будет находиться на пересечении горизонтальной
проекции А'C
c горизонтальной проекцией линии (1'-2');
фронтальная
проекция К"
определится по линии связи;
соединив точки B
и К,
получим отрезок BК,
который будет являться искомой линией пересечения.
|
| 4) |
Показать
видимость сторон треугольников в проекциях :
|
видимость сторон треугольников определяется способом конкурирующих
точек;
видимость проекций А'C' и B'N'
относительно горизонтальной плоскости проекций П1
определяется конкуренцией точек 3"
и 4",
а видимость проекций А"C"
и M"N"
относительно фронтальной плоскости проекций П2
определяется конкуренцией точек 1'
и 5'.
|
| |
