ВОЛНОВАЯ ОПТИКА 18. ИНТЕРФЕРЕНЦИЯ СВЕТА

Содержание Назад Далее

18. ИНТЕРФЕРЕНЦИЯ СВЕТА

Интерференция (от лат. Inter - взаимно, ferio - ударяю) - взаимное усиление или ослабление двух (или большего числа) волн при их наложении друг на друга при одновременном распространении в пространстве.

Интерференция - это одно из основных свойств волн любой природы: упругих (15), электромагнитных (16), в том числе и световых (16.5).

18.1. Интерференция от двух монохроматических источников одинаковой частоты

Изобразим два точечных источника S₁ и S₂, излучающих монохроматические световые волны одинаковой частоты ω. Проанализируем, от чего зависит интенсивность света в точке пространства, удаленной от первого источника на расстояние r₁, а от второго - на r₂.

Пусть векторы E₁ и E₂ обеих световых волн колеблются в одной плоскости, тогда:

Т.к. r₁= const, r₂= const, то в точке наблюдения каждая световая волна см. (16.1.2.2) возбуждает свое гармоническое колебание:

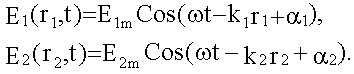
Амплитуда результирующего колебания при сложении колебаний одинаковой частоты и одинакового направления была найдена в (14.3.2):

.

Интенсивность найдем, усреднив это выражение по времени:

,

здесь - разность фаз колебаний, возбуждаемых в точке наблюдения источником S₁ и S₂.

 

18.1.1. Некогерентные волны

Если <Cosδ> = 0, то I = I₁ + I₂- интенсивности складываются.

Такая ситуация наблюдается, если S₁ и S₂ - независимые источники, для них α₁ и α₂ у разных цугов (16.5.5) разные, длительность цуга ~ 10^-8 с. При усреднении по промежутку времени ~ 10^-1 с (время, характеризующее инерционность человеческого глаза) <Cosδ> = 0. Такие волны называют некогерентными.

 

 

18.1.2. Когерентные волны

Когерентные световые волны получают, разделив волну от одного источника на две. Эти две части одной волны уже будут когерентны ( α₁ = α₂, в пределах каждого цуга).

Тогда <Cosδ> = Cosδ = const, при фиксированных r₁ и r₂, следовательно:

.

 

18.1.2.1. Условия максимума и минимума на разность фаз δ

 

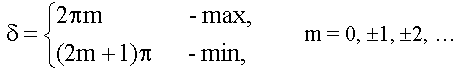
18.1.2.2. Оптическая разность хода

Пусть для простоты, начальные фазы α₁ и α₂ интерферирующих волн равны нулю, тогда:

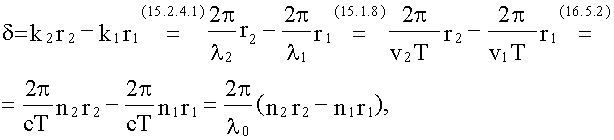
здесь λ₀ = cT - длина световой волны в вакууме.

Оптической разностью хода называют величину:

.

Тогда:

.

18.1.2.3. Условия максимума и минимума на оптическую разность хода

Из (18.1.2.1.) и (18.1.2.2.):

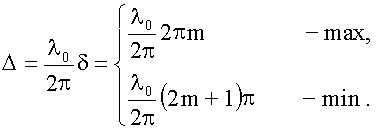
После сокращения получим условия на Δ:

 

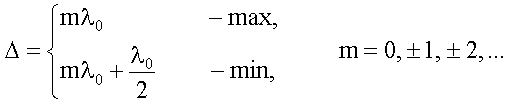
18.1.2.4. Положение максимумов и минимумов при интерференции от двух источников

S₁ и S₂ - когерентные источники света, имеющие одну и ту же начальную фазу колебаний.

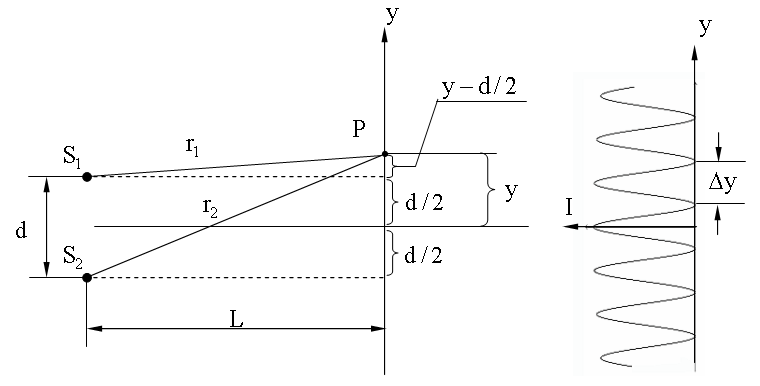
Пусть показатели преломления n₁ = n₂ = 1, тогда оптическая разность хода Δ = r₁ - r₂. Из рисунка следует, что

Обычно L/d ~ 10³, с учетом этого r₁ + r₂ ≈ 2L, тогда:

,

откуда

.

Положения максимумов получим, наложив на Δ условие максимума, см. (18.1.2.3).

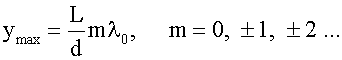
Аналогично - для минимумов:

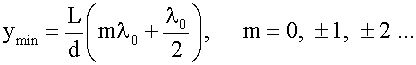
Расстояния между минимумами и максимумами одинаковы:

.

Сибирская государственная геодезическая академия (СГГА), 2003.