ВОЛНОВАЯ ОПТИКА 19. ДИФРАКЦИЯ СВЕТА

Содержание Назад Далее

19.4.4. Дифракционная решетка как спектральный прибор

Из условия главного максимума (19.4.1)

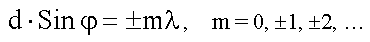
видно, что положение главного максимума зависит от длины волны λ. Зная постоянную решетки d, измерив на опыте угол φ, под которым находится максимум известного порядка m можно из условия главного максимума определить длину волны λ.

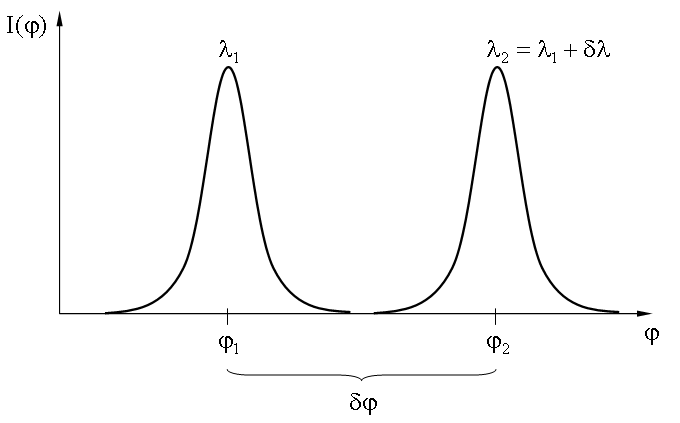
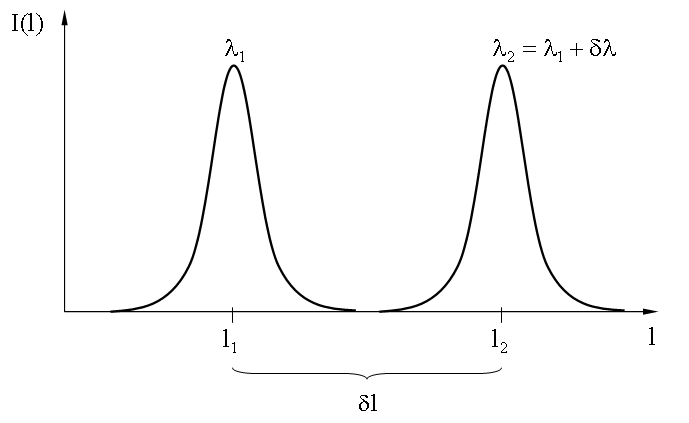
Если в получаемом спектре присутствуют две линии, длины волн которых λ₁ и λ₂ = λ₁ + δλ незначительно отличаются, то возможность их раздельного восприятия определяется двумя причинами:

а) угловым расстоянием между максимумами;

б) их шириной.

Угловое расстояние между максимумами увеличивается с уменьшением d - постоянной решетки (это следует из условия главного максимума). Ширина максимумов определяется положением добавочных минимумов, ближайших к главным максимумам (19.4.2.2.) и уменьшается с увеличением N - числа щелей решетки, принимающих участие в образовании главного максимума.

19.4.4.1. Угловая дисперсия дифракционной решетки

По определению, угловой дисперсией D называется величина:

.

Здесь и далее до конца этой главы, δ - знак дифференциала, т.к. буква d используется - она обозначает постоянную решетки.

В определении угловой дисперсии δλ - разность длин волн двух соседних линий, δφ - соответствующая разность углов, под которыми наблюдаются главные максимумы.

Выразим угловую дисперсию через постоянную решетки d, порядок спектра m и угол φ, под которым наблюдается максимум. Для этого найдем дифференциал от правой и левой части условия главного максимума (19.4.1):

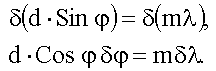
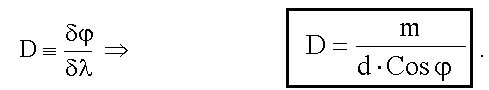
При малых φ Cosφ ≈ 1 и

.

19.4.4.2. Линейная дисперсия

,

где l - расстояние вдоль экрана наблюдения, δl - расстояние между линиями на экране.

При наблюдении дифракции с помощью собирающей линзы при малых углах (φ << 1) из рисунка, приведенного ниже, можно найти связь линейной и угловой дисперсии:

,

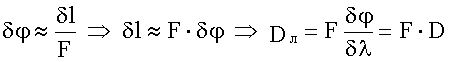
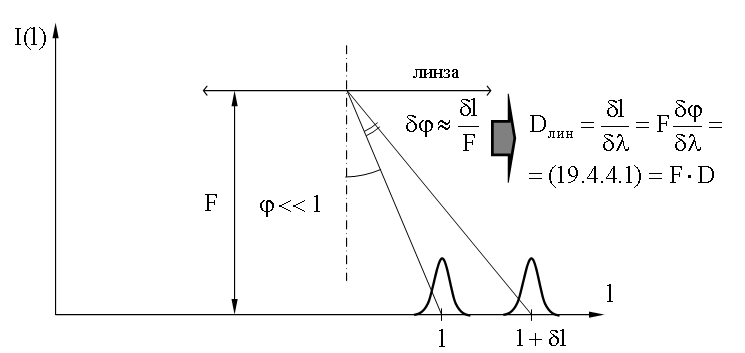
Если наблюдение дифракционной картины ведется без линзы, на большом расстоянии L от решетки, то тогда при малых углах

.

 

19.4.4.3. Разрешающая сила дифракционной решетки

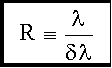
Здесь δλ - минимальная разница в длинах волн соседних спектральных линий, при которой эти линии еще можно наблюдать раздельно.

19.4.4.3.1. Критерий Релея

определяет величину δλ в соответствии с рисунком, представленным ниже.

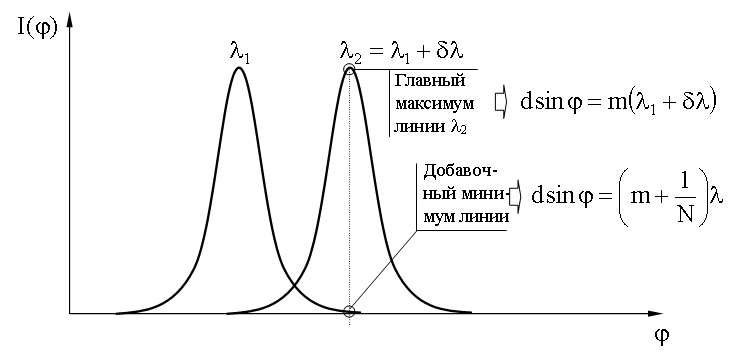
Считают, что линии разрешены, если главный максимум линии λ₁ + δλ и добавочный минимум линии λ₁ совпадает, следовтельно:

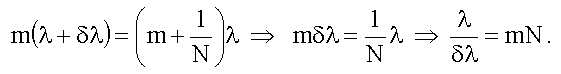
По определению (19.4.4.2)

.

В результате получим:

.

Разрешающая сила R есть величина, обратная относительной погрешности определения длины волны. Она показывает, во сколько раз длина волны λ больше минимально возможной абсолютной погрешности δλ.

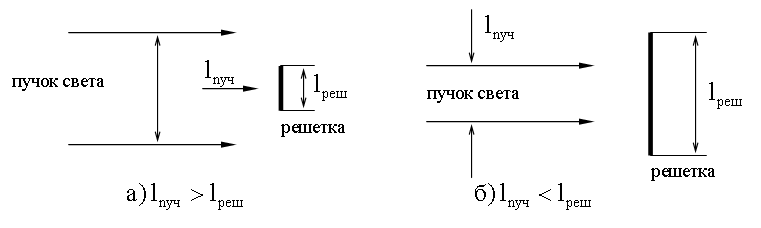
Подчеркнем, что N в формуле для разрешающей силы - это число щелей, принимающих участие в образовании главного максимума порядка m. Если поперечный размер падающего на решетку пучка света l_n больше длины решетки l_реш, то N = l_реш/d, d - постоянная решетки.

Если же l_пуч < l_реш , то N = l_пуч/d.

Кроме того, предполагается, что колебания от всех N щелей когерентны.

19.4.4.4. Разрешающая сила решетки для цуга волн. Соотношение между длиной цуга δx и точностью определения волнового числа δk.

Пусть на решетку по нормали падает цуг волн, протяженностью δx (ось x - вдоль направления распространения цуга).

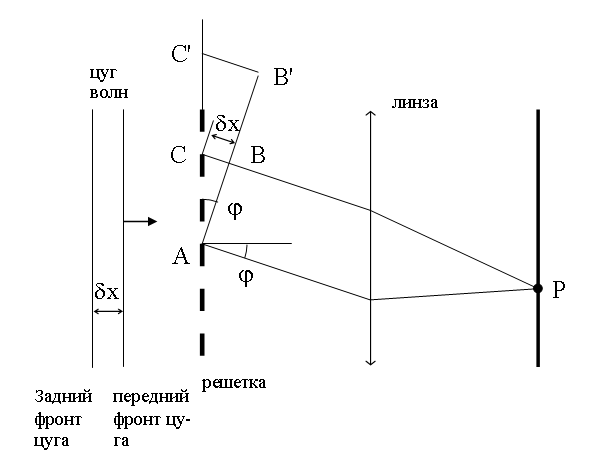
Нетрудно сообразить, что в образовании дифракционных максимумов под углом φ , удовлетворяющим условию главного максимума (19.4.1) d · Sinφ = λm будет участвовать лишь часть решетки AC шириной:

.

Происходит это потому, что в силу таутохронности линзы времена распространения вторичных волн в точку P из точек A и B одинаковы. Следовательно, в этот момент, когда до точки B дойдут вторичные волны из точки С, возбужденные передним фронтом цуга, точку A будет проходить его задний фронт. Значит, число щелей решетки, принимающих в данном случае участие в образовании максимума порядка m будет равно:

.

Но d · Sinφ = λm , тогда

,

Из определения разрешающей силы (14.4.4.3)

.

В соответствии с критерием Релея (14.4.4.3.1)

,       значит,       .

Подставив сюда N = N_m = δx/mλ, получим для δ λ:

.

Выразим λ и δ λ через волновое число k (15.2.4)

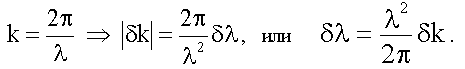
В результате получим:

.

Мы заменили знак равенства на знак "больше или равно", т.к. наши рассуждения проводились для предельно возможной точности определения длины волны δλ, или соответствующей ей точности определения волнового числа δk.

Сибирская государственная геодезическая академия (СГГА), 2003.