ГЕОМЕТРИЧЕСКАЯ ОПТИКА

	ВОЛНОВАЯ ОПТИКА 19. ДИФРАКЦИЯ СВЕТА

Содержание	Назад	Далее

19.3.2.3. Зависимость интенсивности дифракционной картины от угла дифракции φ

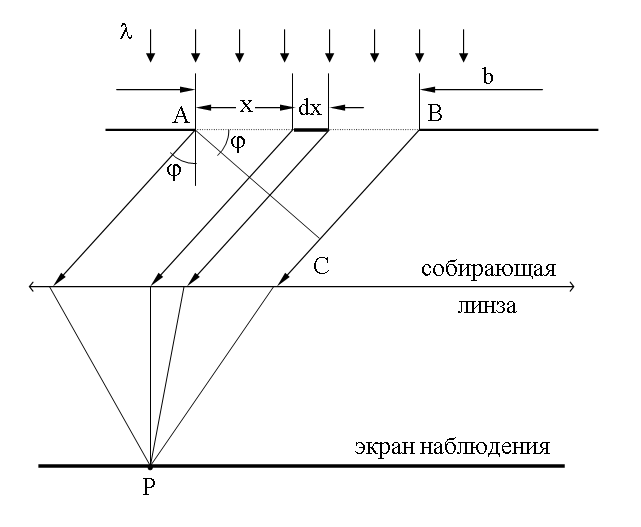
Разобьем щель на полоски шириной dx и изобразим векторную диаграмму колебаний, посылаемых этими полосками в точку наблюдения P. При φ = 0 колебания от всех полосок будут иметь одинаковую фазу. Результирующее колебание в точке P получится в результате сложения сонаправленных бесконечно малых векторов. Векторная диаграмма (14.3) в этом случае будет иметь вид вектора длиной A₀.
Для колебаний приходящих от щели в точку наблюдения P, расположенную под углом φ, векторная диаграмма имеет вид дуги окружности длиной A₀.


Замыкающий эту дугу вектор A_щ является амплитудой результирующего колебания от щели при произвольном угле φ. Фазовый угол δ соответствует максимальной разности хода, равной Δ = b Sinφ . Так как

,   см. (18.1.2.2), то

.

Величину вектора A_щ найдем из геометрических соображений.
      (по определению радианной меры угла).
Из треугольника COB:
.
Исключив R получим:
.
Интенсивность (16.5.4.) пропорциональна квадрату амплитуды, следовательно:
.
Учитывая связь δ с разностью хода Δ, получим связь интенсивности дифрагировавшего света с параметрами разбираемой задачи:
.
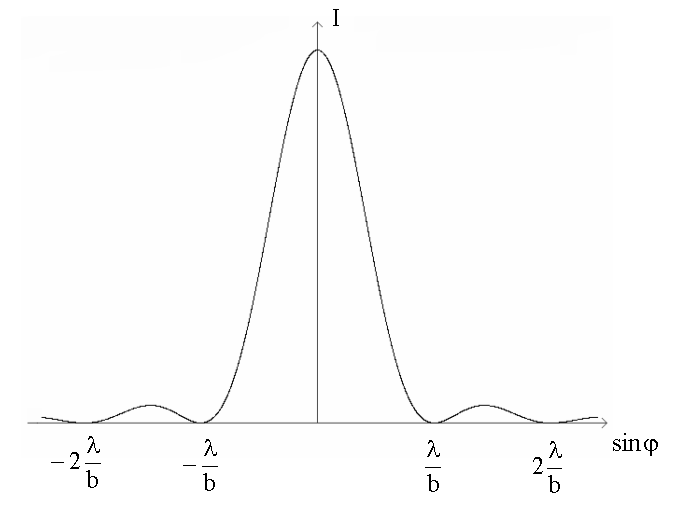
Здесь I₀ - интенсивность при φ = 0.
График этой функции в осях I - Sinφ имеет следующий вид:

19.4 Дифракционная решетка

- это совокупность большого числа одинаковых щелей, отстоящих друг от друга на одно и то же расстояние. Расстояние d между соответственными точками соседних щелей называют периодом решетки:
d = a + b.

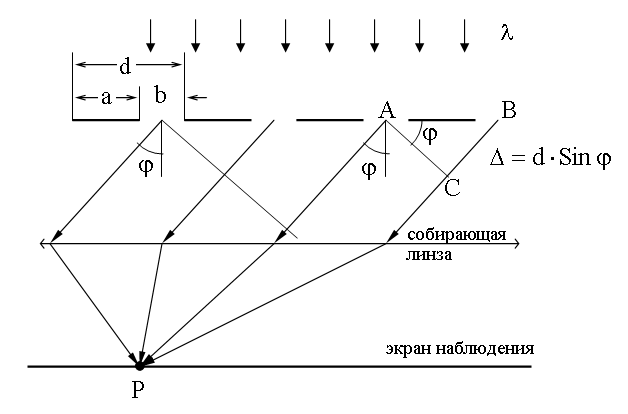
19.4.1. Условие главного максимума для дифракционной решетки

Пусть на дифракционную решетку с числом щелей N падает по нормали параллельный пучок света (плоская волна, 15.1.7) с длиной волны λ. Между экраном и решеткой поместим собирающую линзу. Экран расположим в фокальной плоскости линзы. По принципу Гюйгенса-Френеля (19.2) для нахождения амплитуды результирующего колебания в какой-либо точке P экрана наблюдения надо найти результат интерференции всех вторичных волн, с учетом их фаз и амплитуд. Линза собирает в точке P все параллельные лучи, идущие от решетки под углом φ.
Каждая щель создает колебания с амплитудой зависящей от φ (19.3.2.3).
.
Разность хода лучей, идущих от соответственных точек соседних щелей найдем из треугольника ABC:
.
При выполнении условия максимума (18.1.2.3)
,
таким образом, условие главного максимума для дифракционной решетки будет иметь следующий вид:

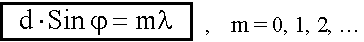
Целое число m называют порядком максимума. Колебания от соседних щелей при выполнении условия максимума в точку P будут приходить в одинаковой фазе. Результирующая амплитуда A_р, создаваемая в точке P решеткой будет в N раз больше амплитуды от одной щели:
.
Интенсивность света (16.5.4):

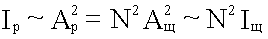
будет в N² раз больше, чем интенсивность I_щ, создаваемая одной щелью.

19.4.2. Зависимость интенсивности дифракционной картины решетки от угла дифракции φ

Амплитуда результирующего колебания от N щелей, A_p(φ), есть результат многолучевой интерференции (18.3). Таким образом:
.
Здесь δ - разность фаз колебаний, идущих в точку P от соответственных точек соседних щелей. Выразим δ через Δ (18.1.2.2), а Δ из треугольника ABC:

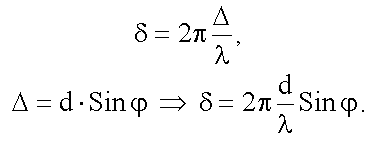
Подставив A_щ, полученную в (19.3.2.3), получим зависимость амплитуды результирующего колебания, создаваемого решеткой для угла φ:
.
Для интенсивности (16.5.4) получим:
.
Здесь I₀ - интенсивность, создаваемая одной щелью при φ = 0, первая дробь учитывает зависимость от интенсивности от φ одной щели, а вторая учитывает результат многолучевой интерференции N щелей.
При выполнении условия главного максимума d·Sinφ = mλ вторая дробь после раскрытия неопределенности по правилу Лопиталя дает N². Таким образом, интенсивность в максимуме, как и было показано в (19.4.1), в N² раз больше интенсивности, создаваемой одной щелью.

19.4.2.1. Минимумы интенсивности дифракционной картины решетки

Формально получить условия на φ при которых будут наблюдаться минимумы можно, если проанализировать на минимум только что полученное выражение I(φ). Анализ дает следующие результаты:

а) - это условие минимума для щели (19.3.2.2);

б) - это условие главного минимума для решетки. При выполнении этого условия колебания от соседних щелей приходят в точку P в противофазе и попарно гасят друг друга;

в) - целое число не кратное N.

Это условие добавочных минимумов. При k' кратном N получим условие максимума.
При выполнении условия добавочных минимумов векторная диаграмма сложения колебаний от N щелей замыкается: конец N-го вектора попадает в начало 1-го и результирующая амплитуда равна нулю. На рисунке ниже изображена эта ситуация для N = 6 (рис. а), k' = 1 и k' = 2 (рис. б). При k' = 2 векторы A₁ и A₄, A₂ и A₅, A₃ и A₆ расположены в одном месте.

19.4.2.2. Добавочные минимумы, ближайшие к главным максимумам

Если в условии добавочных минимумов (19.4.2.1,в) положить k' = 1, N ±1, 2N ±1,…, т.е. k' = mN ±1, m = 0, 1, 2, …, то получим условие для добавочных минимумов, ближайших к главным максимумам порядка m:

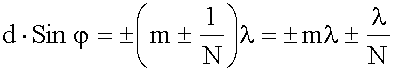
При разности хода d·Sinφ равной ±mλ наблюдается главный максимум порядка m. Добавка к разности хода величины λ/N дает условие минимума, ближайшего к главному максимуму. Эта добавка тем меньше, чем больше N - число щелей решетки, принимающих участие в образовании интерференционной картины. У хороших решеток d ≈ 10^-6 м и при длине решетки l_р= 1 см число щелей N = l_р/d = 10000, что дает очень узкие главные максимумы, необходимые в спектральных приборах.

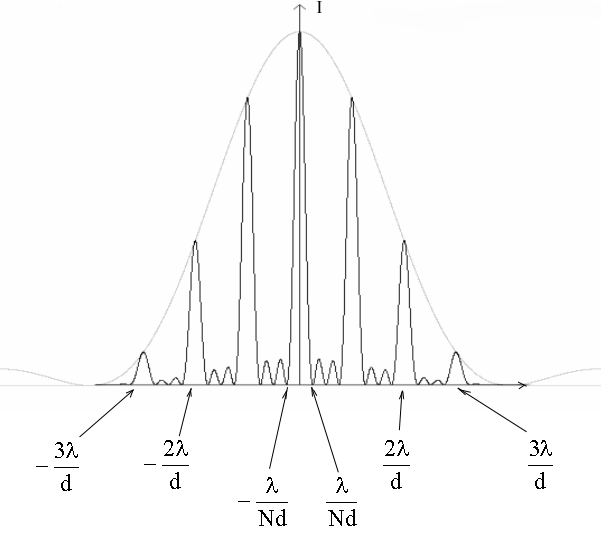
19.4.3. График интенсивности I_p(Sinφ )

Для наглядности графика возьмем решетку с очень малым числом щелей, N = 4. Пусть, для определенности, постоянная решетки d в четыре раза больше ширины щели b, т.е. d = 4b, а длина волны λ = b/2. Найдем значения Sinφ , при которых будут наблюдаться максимумы и минимумы от нашей решетки:
Минимумы для щели (19.4.2.1,а):

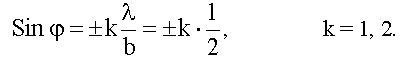
Главные максимумы решетки (19.4.1):

Главные минимумы решетки:

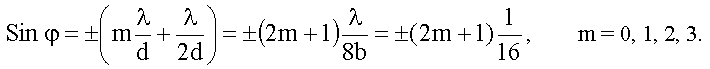
Добавочные минимумы решетки:

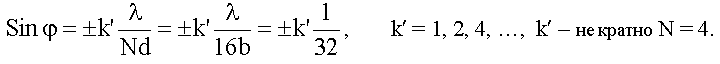
Зависимость интенсивности дифракционной картины от Sinφ изображена на рисунке (расположенном ниже) сплошной линией. Бледная линия - огибающая дифракционной картины - это интенсивность дифракционной картины от одной щели, помноженная на N² = 4² = 16.