ВОЛНОВАЯ ОПТИКА 19. ДИФРАКЦИЯ СВЕТА

Содержание Назад Далее

19. ДИФРАКЦИЯ СВЕТА

Дифракция (от лат. difractus - преломленный) в первоначальном смысле - огибание волнами препятствий, в современном, более широком смысле - любые отклонения при распространении волн от законов геометрической оптики (17.1).

Причина дифракции, как и интерференции (18), - суперпозиция волн, которая приводит к перераспределению интенсивности. Если число интерферирующих источников конечно, то говорят об интерференции волн (18). При непрерывном распределении источников говорят о дифракции волн.

Дифракция проявляется у волн любой природы.

19.1 Дифракция Френеля и Фраунгофера

Если λ - длина волны, b - размеры препятствия, L - расстояние от препятствия до точки наблюдения, то различают следующие ситуации:

 

19.2. Принцип Гюйгенса-Френеля

Строгое решение любой дифракционной задачи для световых волн сводится к нахождению решения уравнений Максвелла (13.4.) с соответствующими граничными условиями.

В оптике большое значение имеет приближенное решение дифракционных задач, основанное на принципе Гюйгенса-Френеля:

1. Каждая точка, до которой доходит волна, служит источником вторичных сферических волн, огибающая которых дает положение волнового фронта в следующий момент времени (Х. Гюйгенс, 1678 г.).
   
   
2. Амплитуда результирующей волны в любой точке пространства может быть найдена как результат интерференции всех вторичных волн, с учетом их фаз и амплитуд (О. Френель, 1818 г
.).

 

19.2.1. Математическая формулировка принципа Гюйгенса-Френеля

Пусть S - волновая поверхность, не закрытая препятствием, P - точка наблю-дения. Тогда элемент поверхности dS возбудит в точке P колебание:

.

Результирующее колебание:

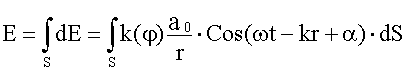
Здесь k( φ) определяет зависимость амплитуды dE от угла между нормалью к площадке dS и направлением на точку P. Множитель a0 дает амплитуду светового колебания в том месте, где находится dS. Величины ω и k - круговая частота и волновое число сферической волны (15.1.7.), распространяющейся от элемента dS.

 

19.3. Зоны Френеля

Вычисление интеграла в пункте (19.2.1.) в общем случае - трудная задача.

В случаях, если в задаче существует симметрия, амплитуду результирующего колебания можно найти методом зон Френеля, не прибегая к вычислению интеграла.

Пусть от источника света S распространяется монохроматическая сферическая волна, P - точка наблюдения. Через точку O проходит сферическая волновая поверхность. Она симметрична относительно прямой SP. Разобьем эту поверхность на кольцевые зоны I, II, III и т.д. так, чтобы расстояния от краев зоны до точки P отличались на λ/2 - половину длины световой волны. Это разбиение было предложено O. Френелем и зоны называют зонами Френеля.

Что дает такое разбиение для расчета интенсивности в точке P? Возьмем произвольную точку 1 в первой зоне Френеля. В зоне II найдется, в силу правила построения зон, такая соответствующая ей точка, что разность хода лучей, идущих в точку P от точек 1 и 2 будет равна λ/2. Вследствие этого колебания от точек 1 и 2 погасят друг друга в точке P.

Из геометрических соображениях следует, что при не очень больших номерах зон их площади примерно одинаковы. Значит каждой точке первой зоны найдется соответствующая ей точка во второй, колебания которых погасят друг друга. Амплитуда результирующего колебания, приходящего в точку P от зоны с номером m, уменьшается с ростом m, т.е.

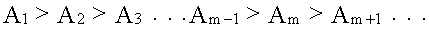
Происходит это из-за увеличения с ростом m угла между нормалью к волновой поверхности и направлением на точку P. Значит гашение колебаний соседних зон будет не совсем полным.

19.3.1. Дифракция Френеля на круглом отверстии

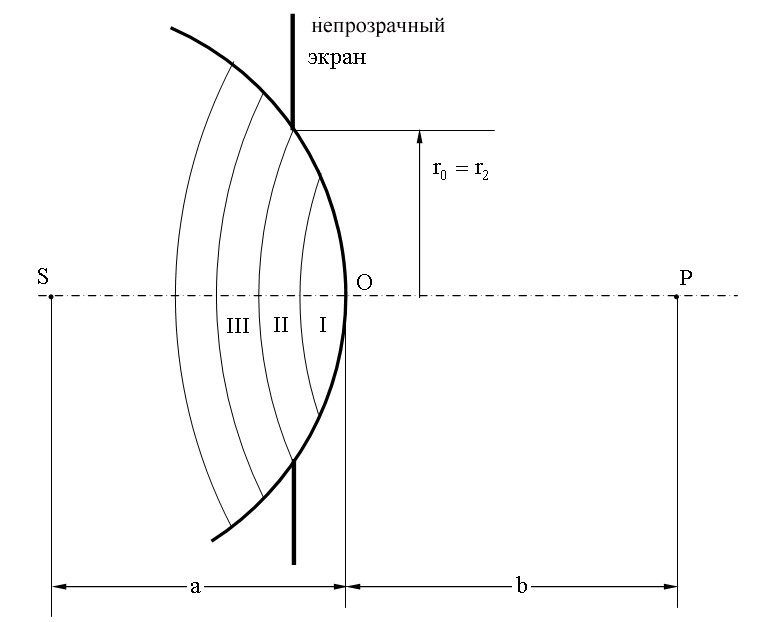
Пусть на пути сферической световой волны, испускаемой источником S, расположен непрозрачный экран с круглым отверстием радиуса r₀. Если отверстие открывает четное число зон Френеля, то в точке P будет наблюдаться минимум, так как все открытые зоны можно объединить в соседние пары, колебания которых в точке P приблизительно гасят друг друга.

При нечетном числе зон в точке P будет максимум, так как колебания одной зоны останутся не погашенными.

Можно показать, что радиус зоны Френеля с номером m при не очень больших m:

.

Расстояние "a" примерно равно расстоянию от источника до преграды, расстояние "b" - от преграды до точки наблюдения P.

Если отверстие оставляет открытым целое число зон Френеля, то, приравняв r₀ и r_m, получим формулу для подсчета числа открытых зон Френеля:

.

При m четном в точке P будет минимум интенсивности, при нечетном - максимум.

19.3.2. Дифракция Фраунгофера на щели

В случае дифракции Фраунгофера параметр b²/(Lλ ) << 1 (19.1). Это значит, что если размер препятствия b ~ λ, то расстояние до экрана наблюдения L >> b.

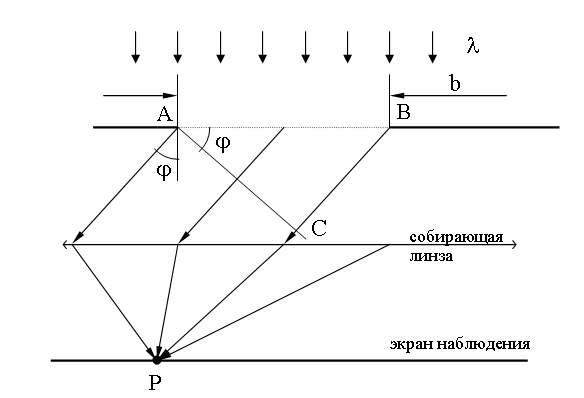
Пусть на длинную щель шириной b падает плоская монохроматическая волна с длиной λ.

Поместим между щелью и экраном наблюдения линзу так, чтобы экран наблюдателя находился в фокальной плоскости линзы. Линза позволяет наблюдать на экране дифракцию в параллельных лучах (L → ∞ ).

19.3.2.1. Таутохронность линзы и ее следствия

Собирающая линза обладает свойством, называемым таутохронностью: лучи, идущие от волновой поверхности AC до точки наблюдения P имеют одинаковую оптическую длину. Таким образом результат суперпозиции вторичных волн, который определяет амплитуду колебаний световой волны в точке P (см. 19.2), зависит от разности хода, набегающей в треугольнике ABC.

19.3.2.2. Определение положений максимумов и минимумов методом зон Френеля

Для нахождения положений максимумов и минимумов интенсивности воспользуемся методом зон Френеля (19.3): разобьем сторону BC на отрезки длиной λ/2.

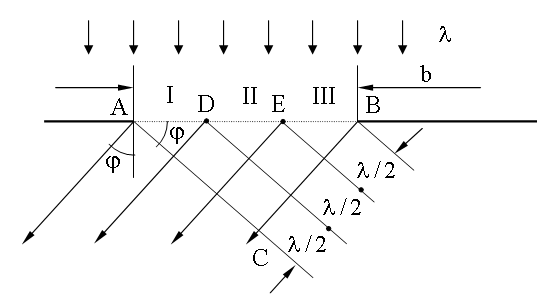
Из концов этих отрезков проведем линии, параллельные фронту вторичной плоской волны, идущей под углом φ. Эти линии разобьют AB - фронт первичной плоской волны на зоны Френеля. На рисунке их изображено три: AD, DE и EB. Число зон Френеля k зависит от λ и длины отрезка BC = b Sinφ . Если k целое, то

.

При четном числе зон Френеля k = 2m, где m = ±1, ±2... все зоны можно разбить на соседние пары, которые гасят друг друга (19.3). Следовательно условие минимума при дифракции Фраунгофера на щели имеет вид:

При нечетном k = 2m + 1 одна зона остается без пары и ее колебания не будут погашены, следовательно, условие максимума при дифракции Фраунгофера на щели будет иметь вид:

.

Обратим внимание, что условия формально противоположны условиям максимумов и минимумов (18.1.2.3) при интерференции от двух источников.

 

Сибирская государственная геодезическая академия (СГГА), 2003.