ПОЛЯРИЗАЦИЯ СВЕТА

	ВОЛНОВАЯ ОПТИКА 20. ПОЛЯРИЗАЦИЯ СВЕТА

Содержание	Назад	Далее

20.5. Поляризация при отражении и преломлении

Если на границу раздела двух сред падает под углом, отличным от нуля, естественный свет, то отраженная и преломленная световая волна будут частично поляризованы.

20.5.1. Формулы Френеля

На рисунке изображены и обозначены соответствующими значками составляющие векторов напряженности электрического поля падающей волны , отраженной волны , преломленной волны .

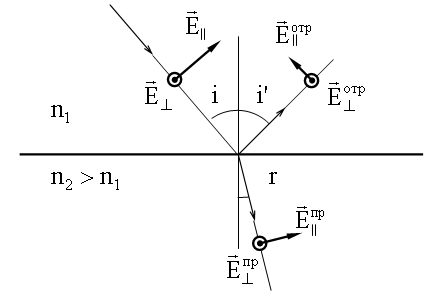
Относительные значения этих величин следуют из граничных условий, налагаемых на электрическое и магнитное поле световой волны. Формулы, связывающие компоненты векторов , были впервые получены О. Френелем и носят название формул Френеля:

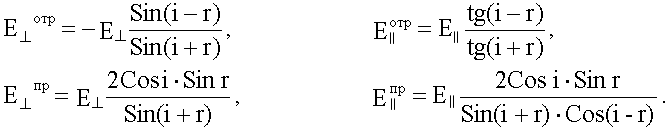
Эти формулы и позволяют рассчитать степень поляризации (20.3.1) отраженной и падающей волны для произвольного угла падения.

20.5.2. Закон Брюстера

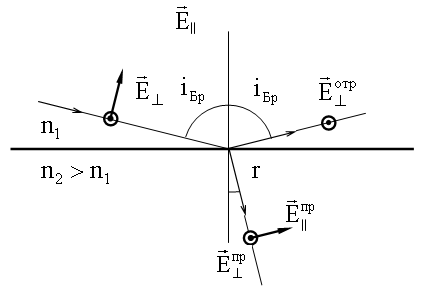
Пусть угол падения i таков, что отраженный луч перпендикулярен преломленному, т.е. r = π/2 - i_Бр. Это условие называют условием Брюстера (см. рисунок ниже), а угол - углом Брюстера - i_Бр.

Используя закон преломления
     (17.1.3.),
получим формулу, определяющую угол Брюстера:
.
При выполнении условия Брюстера i + r = π/2, тогда из формулы Френеля для получим:

Таким образом, при выполнении условия Брюстера, отраженный свет будет полностью поляризован в плоскости, перпендикулярной плоскости падения.
Это утверждение носит название закона Брюстера.
Закон Брюстера имеет простое объяснение. Отраженная световая волна появляется за счет излучения электронов среды, совершающих вынужденные колебания под действием вектора преломленной волны. Это излучение имеет направленный характер (16.4.2.3): его интенсивность равна нулю в направлении колебаний зарядов. Направим под углом Брюстера на границу раздела плоско поляризованную волну с вектором , лежащим в плоскости падения.

На рисунке изображена диаграмма направленности излучения, возбужденного вектором . Нулевой минимум этой диаграммы при выполнении условия Брюстера совпадает по направлению с отраженным лучом.
Если вектор падающей волны направить перпендикулярно плоскости падения (рисунок ниже), то направление колебаний электронов будет перпендикулярно плоскости падения. Тогда диаграмма направленности будет развернута своим максимумом в направлении отраженного луча (рисунок ниже). Напомним, что пространственная форма диаграммы похожа на бублик без дырки (16.4.2.3).

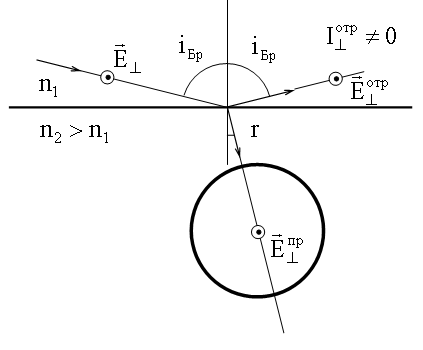
20.6. Двойное лучепреломление

Как уже упоминалось в (17.1.2.), закон преломления может не выполняться в анизотропных средах. Действительно, этот закон утверждает, что:
,       где n₁ и n₂ - постоянные для данных веществ величины.
Но
     (19.3.2),
где E₀ - напряженность электрического поля в вакууме, а E - в веществе. Поле в веществе E < E₀, т.к. диэлектрик поляризуется и создает поле E', направленное навстречу E₀. В свою очередь поле E' пропорционально вектору поляризации (9.13.3), а величина вектора пропорциональна сумме дипольных моментов молекул (9.13.2). Дипольный же момент – это произведение заряда q на расстояние между зарядами r (9.13.1.1.). Если молекула несимметрична, то величина ее дипольного момента зависит от ее ориентации относительно вектора напряженности электрического поля. Следовательно, показатель преломления n будет зависеть от направления вектора световой волны. В этом и состоит нарушение закона преломления.

20.6.1. Модель двояко преломляющего кристалла

Рассмотрим модель кристаллического вещества, в котором "молекулы" в форме эллипсоидов вращения хорошо поляризуются вдоль одной оси. Назовем эту ось оптической осью "кристалла". В направлениях, перпендикулярных этой оси (рисунок ниже), "молекулы" поляризуются хуже.

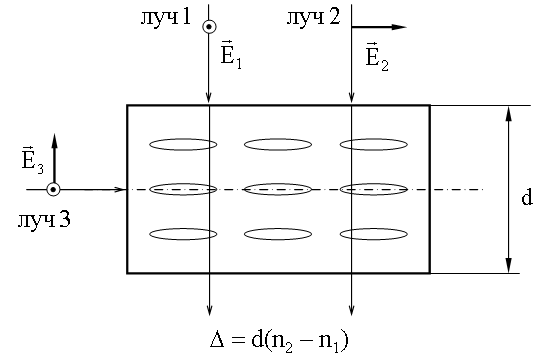
Направим на этот "кристалл" перпендикулярно оптической оси два плоско поляризованных луча света. Пусть у одного луча вектор 1 перпендикулярен длинной оси "молекул" - оптической оси "кристалла", а у другого 2 параллелен оптической оси. Показатели преломления для этих лучей будут разные. В силу приведенных выше рассуждений n₁< n₂. Лучи 1 и 2 после прохождения кристалла толщиной d приобретут оптическую разность хода:
.
С этой разностью хода связана разность фаз (18.1.2.2):
.
При изменении плоскости поляризации света показатель преломления будет изменяться от n₁ до n₂, т. е. n ≠ const!
Направим теперь на наш "кристалл" плоско поляризованный свет, распространяющийся вдоль оптической оси. В силу симметрии "молекул" в плоскости, перпендикулярной оптической оси, показатель преломления теперь не будет зависеть от направления вектора . В данной ситуации при любом своем направлении вектор остается перпендикулярным длинной оси молекул (оптической оси "кристалла"), следовательно, n = const = n₁.
Главным сечением кристалла называют любую плоскость, проходящую через его оптическую ось. Если вектор световой волны перпендикулярен главному сечению, то показатель преломления n = const = n₁ (лучи 1 и 3 на верхнем рисунке).

20.6.1.1. Необыкновенный и обыкновенный луч

Направим на наш кристалл под произвольным углом к оптической оси световую волну с вектором , лежащим в главном сечении (рисунок ниже). Пусть верхняя грань кристалла будет параллельна оптической оси.

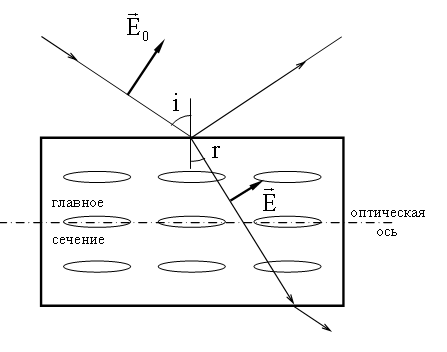
При изменении угла падения i угол преломления r будет изменяться, но отношение
.
Это и есть нарушение закона преломления. Поэтому, такой луч называют необыкновенным, для него показатель преломления не является постоянной величиной, он зависит от направления распространения луча (т.к. с ним связана, в этом случае, ориентация вектора относительно оптической оси кристалла). Максимальная величина показателя преломления обычно обозначается n_e (у нас n_e обозначено как n₂).
Если вектор световой волны направить перпендикулярно главному сечению (см. рисунок в разделе (20.6.1), луч 1), то показатель преломления не будет зависеть от угла падения, т.е. закон преломления будет выполняться. Такой луч называют обыкновенным, а показатель преломления для этого луча обозначают обычно n₀ (у нас n₀ обозначено как n₁).