ВОЛНЫ В УПРУГОЙ СРЕДЕ

	ВОЛНЫ 15. ВОЛНЫ В УПРУГОЙ СРЕДЕ

Содержание	Назад	Далее

15.3. Волновое уравнение

Применяя второй закон Ньютона (4.6) к упругой среде, можно получить дифференциальное уравнение в частных производных, решением которого будет уравнение волны. Логическая схема этого вывода такова:

15.3.1. Вывод закона Гука для бесконечно малого упругого стержня

Выделим элемент упругого стержня, длиной Δx.

Закрепим левую часть этого элемента (второй рисунок), правую сместим на величину Δξ вдоль оси x.

- закон Гука.

Здесь коэффициент k_упр, характеризующий упругость стержня, зависит от материала стержня, его длины и площади сечения.

15.3.1.1. Нормальное напряжение и относительная деформация

Введем:

     - нормальное напряжение,

       - относительная деформация.

При Δx → 0

.

Перепишем , выразив F и Δξ через σ и ε :

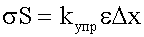
или

.

15.3.1.2. Модуль Юнга

Величина не зависит от длины и сечения стержня, она определяется только упругими свойствами материала, ее называют модулем Юнга материала:

.

15.3.1.3. Закон Гука

Тогда связь нормального напряжения σ и относительной деформации ε будет иметь вид:

.

Это выражение тоже носит название закона Гука.

15.3.2. Вывод волнового уравнения из .

Пусть волна распространяется вдоль упругого стержня. Рассмотрим элемент этого стержня, его длина равна Δx в невозмущенном состоянии. Пусть при распространения волны левая часть этого элемента сместится на величину ξ(x), а правая - на величину ξ(x + Δx), не равную смещению левой части.

.

В нашем примере стержень растянут внешними силами:

Сумма этих сил равна:

.

Домножим и поделим последнее выражение на Δ x. Величина

при Δx → 0 дает вторую производную от "кси" по x, т.е. .

Тогда .

Масса нашего элемента , его ускорение (3.10)

,

тогда преобразуется в

,

или

   - волновое уравнение.

Проверим, будет ли его решением.

Откуда

.

Т.к. (15.2.4), то фазовая скорость упругой продольной волны:

,

и волновое уравнение можно записать в виде:

.

Для волны, распространяющейся в произвольном направлении (15.2.5) волновое уравнение имеет вид:

.