ВОЛНЫ 15. ВОЛНЫ В УПРУГОЙ СРЕДЕ

Содержание Назад Далее

15.4. Энергия упругой волны

Найдем полную механическую энергию (5.8.2) для выделенного нами элемента упругой среды, в которой распространяются упругая продольная волна:

.

Скорость (3.8.2):

,

тогда

.

Потенциальная энергия упругого деформированного стержня:

.

Полная энергия выделенного элемента объемом SΔx будет равна:

.

15.4.1. Плотность энергии упругой волны

.

15.4.1.1. Плотность энергии упругой гармонической волны

15.4.1.1.1. Среднее по времени значение плотности энергии упругой гармонической волны

, это известно из математики, значит:

.

15.4.2. Поток энергии

15.4.3. Плотность потока энергии

15.4.4. Вектор Умова - связь плотности потока энергии с плотностью энергии упругой волны

15.4.5. Интенсивность волны

- это среднее по времени от модуля вектора плотности потока энергии:

.

Для гармонической волны:

.

15.5. Стоячие волны

При наложении двух встречных плоских волн с одинаковой амплитудой возникает колебательный процесс, называемый стоячей волной. При этом переноса энергии не происходит.

15.5.1. Уравнение стоячей волны

Для волны, бегущей по оси x:

.

Для волны, бегущей против оси x:

,    см. (15.2.3), (15.2.4), (15.2.5).

Для простоты мы положили равным нулю значение начальных фаз этих волн. Сумма этих уравнений и дает уравнение стоячей волны:

15.5.1.1. Амплитуда стоячей волны

- это модуль выражения, стоящего перед множителем Cosωt, т.е.

15.5.2. Узлы и пучности

Поверхность, где амплитуда колебаний равна нулю, называют узлами стоячей волны. Для узлов:

Следовательно, координаты узлов:

Поверхность, где амплитуда колебаний достигает максимума, называют пучностями стоячей волны.

Для пучностей:

Координаты пучностей:

15.5.3. Колебания струны, закрепленной с двух концов

В силу граничных условий, заданных закреплением концов струны, уравнение стоячей волны при выборе начала координат на одном из концов струны следует записать через функцию Sin kx, т.е.

.

Тогда условие будет выполнено. Для выполнения граничного условия на другом конце струны мы должны потребовать, чтобы

.

Это приводит к квантованию волнового числа, т.е. k может принимать не любые значения, а только дискретные, определяемые равенством:

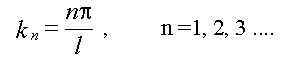
т.к.

то

Вдоль струны должно укладываться целое число полуволн! Из (15.1.7) и мы получаем спектр (набор) частот, на которых может колебаться закрепленная с двух концов струна:

Частота v₁ называется основным током,     v₂ - первым обертоном и т.д.

Сибирская государственная геодезическая академия (СГГА), 2003.