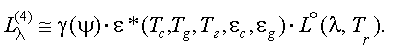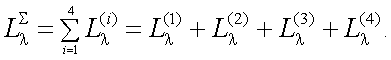2.1. Закон Кирхгофа
Рассмотрим элемент dS поверхности твердого тела, нагретого до температуры Т (рис. 2.1).
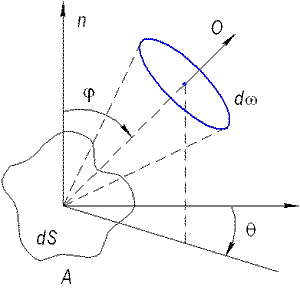
Рис. 2.1. К закону Кирхгофа в теории теплового излучения
Элемент dS излучает в пределах телесного угла ω лучи сложного спектрального состава (сплошной спектр). Если из всего излучения выделить часть, распространяющуюся внутри малого телесного угла dω и интервале длин волн λ, λ + dλ, то мощность dPλ этой части излучения можно представить в следующей форме:
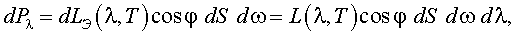 |
(2.1) |
Величина 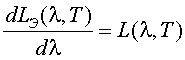 – спектральная плотность яркости теплового излучения.
– спектральная плотность яркости теплового излучения.
Если на этот же элемент поверхности dS излучателя в обратном направлении ОА упадет поток dQ этого же спектрального состава λ, λ + dλ в виде естественного излучения, то часть потока α(λ, Т) dQ будет поглощена, где α(λ, Т) – коэффициент поглощения материала твердого тела, который зависит от свойств вещества, λ и Т.
Рассмотрим теперь систему тел, изолированную от окружающего пространства замкнутой и теплонепроницаемой оболочкой. Эти тела могут состоять из любых материалов с произвольными поверхностями – зеркальными или матовыми – и могут иметь произвольные начальные Т.
Согласно второму началу термодинамики из установившегося температурного равновесия наша система выйти не сможет и, следовательно, любой участок ограждающей стенки получает от окружающих тел столько же энергии, сколько он сам излучает. Иными словами, в пространстве, в котором установилось температурное равновесие, спектральные плотности яркости L0 (λ, Т) для любых λ и Т должны быть одинаковы во всех точках и во всех направлениях.
Функция L0 (λ, Т) оказывается универсальной в том смысле, что она не зависит от материалов, из которых состоит система.
Участок dS поверхности тела, находящегося в замкнутом пространстве при температуре Т, излучает в пределах dω и λ, λ + dλ мощность dP, как отмечено в выражении (2.1). В обратном направлении на участок dS в пределах того dω и λ, λ + dλ падает поток dQ = L0(λ, Т) cosφ dS dω dλ.
Из этого потока площадка dS поглощает часть, равную по условиям равенства излучаемой мощности dPλ.
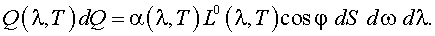 |
(2.2) |
Приравняв эти выражения, получим:
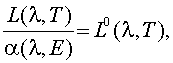 |
(2.2) |
независимо от того, к какому материалу это относится.
Таким образом, исходя из условий термодинамического равновесия, Г.Р. Кирхгоф вывел свой закон, который можно сформулировать так: «отношение спектральной плотности яркости (СПЯ) температурного излучателя к его коэффициенту поглощения является постоянной величиной и не зависит от рода излучателя».
2.2. Закон Планка
Функция L0(A, T), представляющая собой спектральную плотность энергетической яркости (СПЭЯ) тела, у которого α (λ, Т) = 1, была установлена в 1900 г. М. Планком и характеризует СПЭЯ абсолютно черного тела (АЧТ):
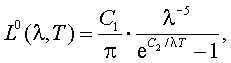 |
(2.4) |
где λ, в см;
С1 = 3,74·10 –12 Вт·см;
С2 = 1,438 см. град.
2.3. Закон Вина
В 1896 г. В. Вин предложил другую формулу закона излучения АЧТ:
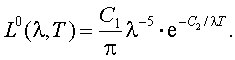 |
(2.5) |
Формула (2.5) получается из закона (2.4) при  .
.
2.4. Закон Релея - Джинса
При 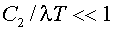 Дж. У. Рэлей и Дж. Джинс [2] получили формулу:
Дж. У. Рэлей и Дж. Джинс [2] получили формулу:
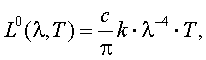 |
(2.6) |
где с – скорость света в вакууме;
k – постоянная Больцмана, численно равная 1,38·10-23 Дж·град-1
Эта формула вытекает из соотношения (2.4) при разложении 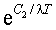 в ряд:
в ряд:
Воспользовавшись двумя членами этого ряда и подставив их в (2.5) получим:
где 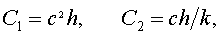
h – постоянная Планка.
Формула (2.6) справедлива в длинноволновой ИК области спектра.
2.5. Закон Стефана - Больцмана
Зависимость интегральной яркости АЧТ от температуры Т была установлена еще до открытия закона Планка. Эмпирически Й. Стефан (1879 г.) и теоретически Л. Больцман (1884 г.) установили, что интегральная яркость АЧТ L0(T) ~T4. Это следует и из формулы Планка, если ее проинтегрировать в пределах λ от 0 до ∞:
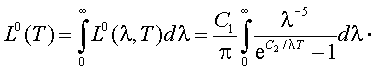 |
(2.7) |
Введем замену переменных:
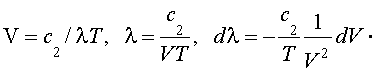 |
(2.7') |
Подставив (2.7´) в (2.7) получим [2]:
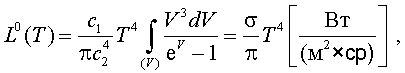 |
(2.8) |
где σ – постоянная Стефана – Больцмана, численно равная σ = 5,67·10-12 Вт/(см2·К4).
2.6. Закон смещения Голицына - Вина
Если формулу Планка продифференцировать по λ и найти длину волны λm максимума СПЭЯ абсолютно черного тела, т. е. значение λm, при которой L0(λ, Т) максимально, то оказывается что искомое значение λm равно:
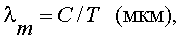 |
(2.9) |
где С = 2898 мкм · К.
Вывод соотношения (2.9) следующий:
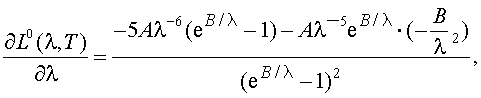 |
(2.9') |
где 
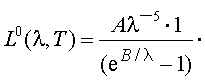
Так как максимум спектральной яркости
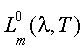 имеет место при
имеет место при 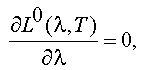
то на основании соотношения(2.9') имеем:
Так как 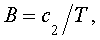 то
то 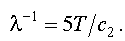
Тогда
Иногда постоянную величину С называют постоянной закона смещения.
Если теперь подставим (2.9) в формулу Планка, то получим связь максимума СПЭЯ АЧТ с температурой Т:
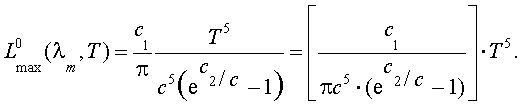 |
(2.10) |
2.7. Энергетические характеристики оптического излучения (сигналов) объектов в ОЭП и С обнаружения, самонаведения и слежения
2.7.1. Энергетические характеристики оптического излучения объектов применительно к ОЭП и С активного и пассивного типов
Рассмотрим энергетические характеристики оптического излучения космического аппарата (КА) и воздушных целей, которые в системах обнаружения формируют полезные сигналы, поскольку эти объекты в наиболее частых случаях являются наблюдаемыми или исследуемыми.
Проанализируем оптическое излучение космических аппаратов применительно к пассивным ОЭС.
В условиях полета КА в околоземном космическом пространстве он находится в световом поле прямого излучения Солнца, диффузного излучения космического фона и подстилающей поверхности Земли. Излучение этих источников отражается поверхностью КА, чем и формирует составляющую отраженного излучения (ОИ) КА. С учетом работ [9, 17] выражение для спектральной плотности энергетической яркости (СПЭЯ) отраженного излучения КА имеет вид:
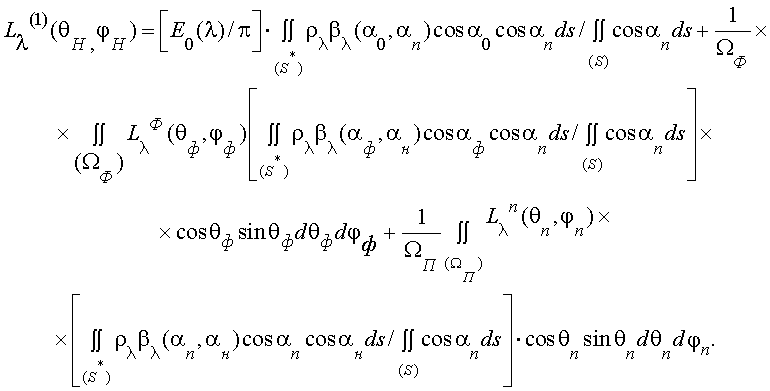 |
(2.11) |
Здесь Е0(λ) –спектральная плотность энергетической освещенности Солнца вне атмосферы;
LλФ(θФ, φФ), LλП(θП, φП) – СПЭЯ соответственно космического фона и подстилающей поверхности в направлении, характеризуемом углами (θФ, φФ) и (θП, φП);
ρλ и βλ – соответственно коэффициент отражения и коэффициент яркости материала покрытия КА на длине волны λ;
S* – часть освещенной и видимой с направления наблюдения поверхности КА;
S – часть видимой поверхности КА;
α0, αН, αФ, αn – углы между нормалью к элементу dS КА и направлениями соответственно на Солнце, наблюдателя, космический фон и подстилающую поверхность.
В связи с условиями теплового режима поверхности КА, который устанавливается, в основном, тепловым излучением Солнца, освещенная часть поверхности КА достаточно сильно нагревается и является источником собственного излучения (СИ). Выражение для СПЭЯ собственного излучения КА имеет вид:
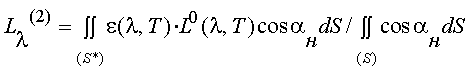 |
(2.12) |
где L0(λ, Т) – СПЭЯ абсолютно черного тела при температуре Т;
ε(λ, Т) – спектральный коэффициент излучения материала обшивки КА.
Источником теплового излучения КА могут быть и его двигательные установки. Если обозначить СПЭЯ собственного излучения двигателя КА через L(3)λ, тогда, учитывая выражение (2.11) и (2.12), СПЭЯ общего оптического излучения КА будет выражаться как сумма всех составляющих:
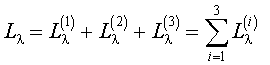 . . |
(2.13) |
Выражения (2.11) ÷ (2.13) справедливы применительно к пассивным ОЭП. Для активных ОЭП, когда наблюдаемая поверхность КА подсвечивается коллимированным излучением оптического квантового генератора, излучение которого когерентно и поляризовано, то характеристикой отражения оптического излучения поверхности КА является матрица отражения (МО) [17, 18]. Поэтому, выражение для энергетической силы произвольно поляризованного отраженного излучения КА имеет вид:
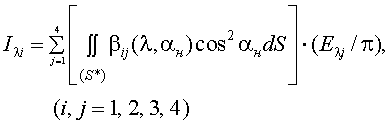 |
(2.14) |
где βij(λ, αн) – матрица отражения элемента dS поверхности КА на длине волны λ и в функции угла αн;
Еλj – вектор-параметр Стокса для энергетической освещенности, создаваемой оптическим излучением ОКГ в месте нахождения КА.
Следует отметить, что компоненты вектор-параметра Стокса
[17] полностью описывают оптическое излучение, т.е. его интенсивность, степень, тип и форму поляризации.
Излучение воздушных целей является основным в работе приборов и комплексов самонаведения или наведения. Поэтому из всех возможных излучений целей необходимо рассмотреть излучение самолетов и вертолетов.
При полете самолета в атмосфере Земли основными источниками его излучения являются:
1) собственное излучение обшивки самолета;
2) отраженное излучение корпуса самолета;
3) собственное излучение реактивной струи двигателя;
4) собственное излучение сопла двигателя.
1. Рассмотрим собственное излучение обшивки самолета.
Физические принципы, на которых базируется методика расчета теплового излучения корпуса самолета, состоят в нагреве обшивки самолета за счет аэродинамического торможения встречного потока воздуха. Уплотнение газовой среды, обтекающее твердое тело, растет с увеличением скорости обтекания и становится существенным уже при числах Маха (М), близких к 1. Абсолютная температура торможения Т*, близкая по своим параметрам к воздуху идеальной газовой среды, при полном торможении в адиабатических условиях определяется широко известной в аэродинамике приближенной формулой [4]:
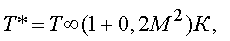 |
(2.15) |
где Т∞ – абсолютная температура газа до торможения.
Тогда, рассматривая собственное излучение обшивки как излучение серого тела, для которого спектральная яркость связана с излучением АЧТ и спектральным коэффициентом излучения ε (λ, Т) по формуле:
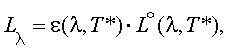 |
(2.16) |
СПЭЯ собственного излучения корпуса получится в виде:
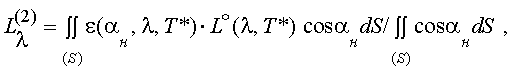 |
(2.17) |
где ε (αн, λ, Т*) – индикатриса коэффициента излучения обшивки корпуса.
Выражение (2.18) упрощается для материалов обшивок, у которых ε (αн, λ, Т*) не зависит от угла αн (изотропный излучатель):
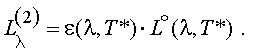 |
(2.17') |
2. Рассматривая самолет в поле прямого излучения Солнца, рассеянного излучения атмосферы и подстилающей поверхности, его СПЭЯ отраженного оптического излучения имеет вид:
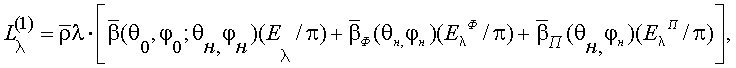 |
(2.18) |
где  – индикатриса коэффициента габаритной яркости (КГЯ) [21] отражения самолета при направленном освещении Солнцем в функции углов его ориентации по отношению к направлению на Солнце (θ0, φ0) и на наблюдателя (θн, φн);
– индикатриса коэффициента габаритной яркости (КГЯ) [21] отражения самолета при направленном освещении Солнцем в функции углов его ориентации по отношению к направлению на Солнце (θ0, φ0) и на наблюдателя (θн, φн);
 – то же при полусферическом освещении соответственно излучением неба как фона и подстилающей поверхности;
– то же при полусферическом освещении соответственно излучением неба как фона и подстилающей поверхности;
Еλ – спектральная энергетическая освещенность, создаваемая прямыми лучами Солнца на той высоте в атмосфере, где осуществляется полет.
Необходимо отметить, что КГЯ 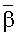 слабо зависит от формы самолета, не зависит от его размеров и функционально связан с эффективной отражающей поверхностью SЭ и эквивалентной поверхностью рассеяния σ [21]:
слабо зависит от формы самолета, не зависит от его размеров и функционально связан с эффективной отражающей поверхностью SЭ и эквивалентной поверхностью рассеяния σ [21]:
 , , |
(2.19) |
где S – площадь проекции самолета в направлении наблюдателя.
3. Собственное излучение реактивной струи и сопла турбореактивного двигателя самолета.
Источником излучения реактивной струи являются нагретые пары Н2О и СО2, являющиеся продуктом сгорания авиационного топлива. Центры полос излучения этих газов сосредоточены на длинах волн λ = 2,7 мкм и λ = 4,3 мкм. Методы расчета излучения струи довольно громоздки, сложны и включают в себя различные виды решений уравнения переноса излучения в неоднородной и неизотермической поглощающей среде на отдельных длинах волн λ с учетом излучения всех отдельных линий полос излучения молекул нагретых паров Н2О и СО2. Обычно определяют отдельно СПЭЯ излучения в полосах поглощения Н2О и СО2, а потом эти составляющие суммируют.
Так, если 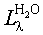 и
и 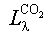 представляют собой СПЭЯ соответственно излучения паров воды и углекислого газа, то общее излучение реактивной струи будет иметь вид:
представляют собой СПЭЯ соответственно излучения паров воды и углекислого газа, то общее излучение реактивной струи будет иметь вид:
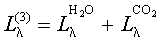 , , |
(2.20) |
4. Источником собственного излучения двигателя самолета является также его сопло. Поверхности деталей во внутренней полости двигателя омываются газовым потоком, нагретым до температуры более 1000 К. Нагретые до такой температуры стенки полости и ее основание излучают как серое тело, коэффициент излучения которого ε ≈ 0,9.
Методы расчета (или моделирования) теплового излучения сопла состоят в построении (воспроизведении) геометрии сопла как полости конической, цилиндрической или другой формы и анализе результата явлений многократных отражений, возникающих в замкнутых полостях, стенки которых неравномерно нагреты и могут иметь различные индикатрисы коэффициентов излучения и отражения. В первом приближении СПЭЯ излучения сопла имеет вид:
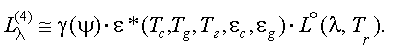 |
(2.21) |
Здесь γ(ψ) индикатриса излучения сопла, которая зависит от формы полости (ψ – угол, отсчитываемый относительно оси сопла);
ε*(Тс, Тg, Тг, εс, εg) – эффективный коэффициент излучения полости на срезе сопла, который является функцией температуры стенок сопла Тс, дна полости Тg и среза газогенератора Тг, а также коэффициентов излучения дна εg и стенок сопла εс.
Учитывая выражения (2.15)÷(2.21), суммарное оптическое излучение самолетов будет иметь вид:
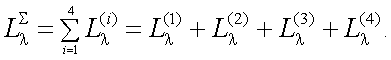 |
(2.22) |
Оптическое излучение вертолетов, как его составляющие, так и суммарное, формируется аналогичным образом.
Применительно к активным ОЭП методика расчета обратно отраженного оптического излучения самолетов и вертолетов базируется на формуле (2.14), полученной для космических аппаратов. Следует заметить, что в квадратных скобках формулы (2.14) находится выражение для матрицы эффективной отражающей поверхности КА (Sij). Что касается самолетов и вертолетов, то для них Sij будет иметь другое значение.


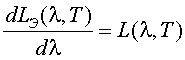 – спектральная плотность яркости теплового излучения.
– спектральная плотность яркости теплового излучения.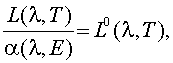
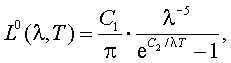
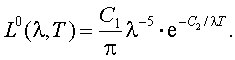
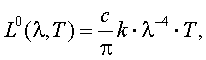

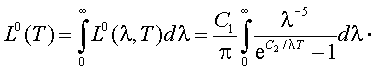
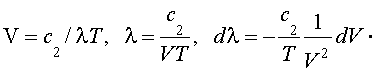
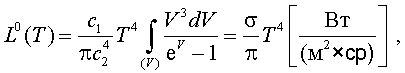
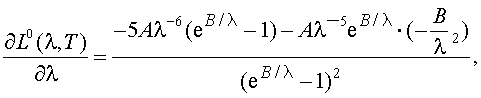

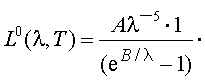
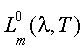 имеет место при
имеет место при 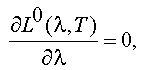
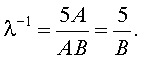
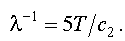
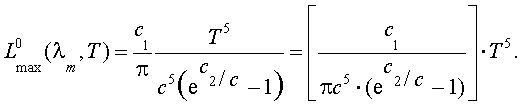
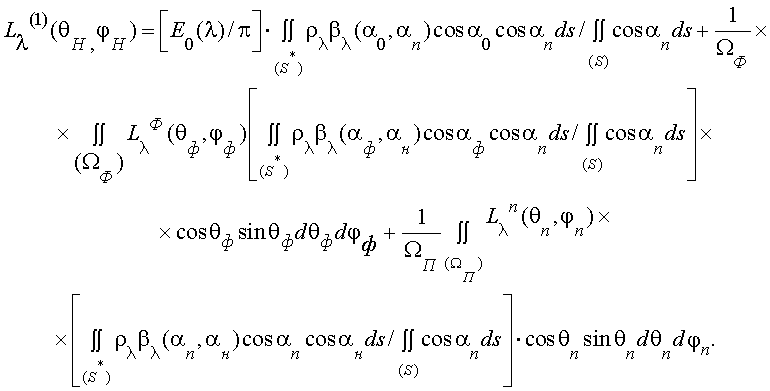
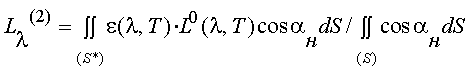
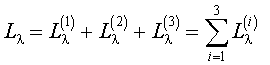 .
.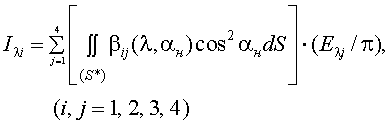
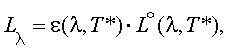
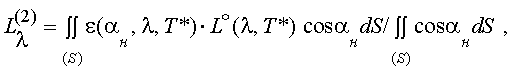
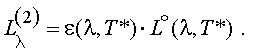
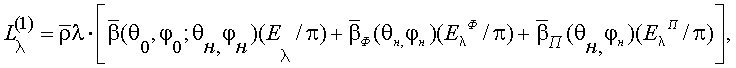
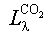 представляют собой СПЭЯ соответственно излучения паров воды и углекислого газа, то общее излучение реактивной струи будет иметь вид:
представляют собой СПЭЯ соответственно излучения паров воды и углекислого газа, то общее излучение реактивной струи будет иметь вид: