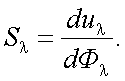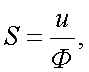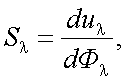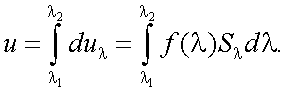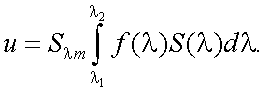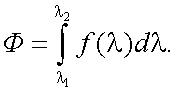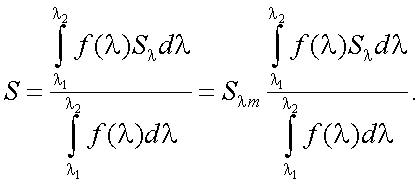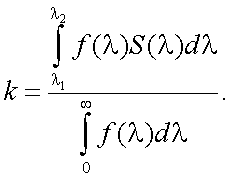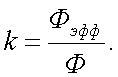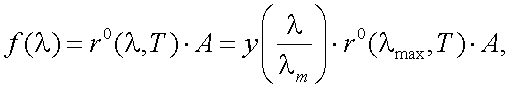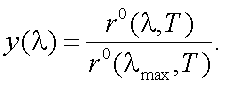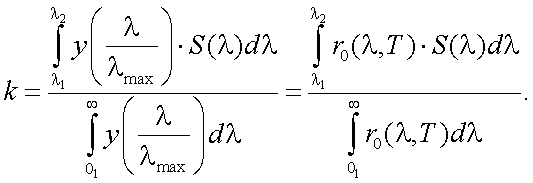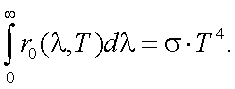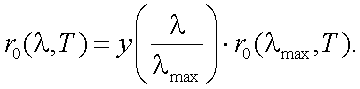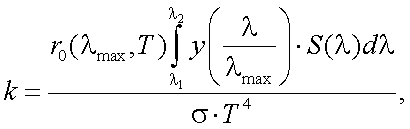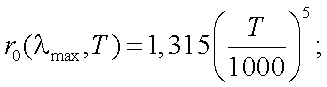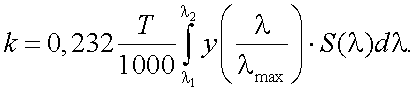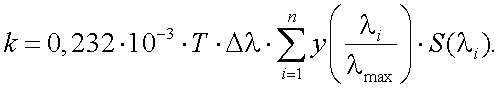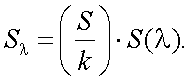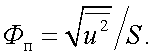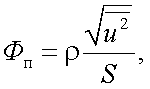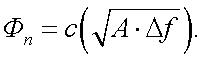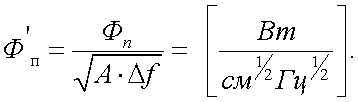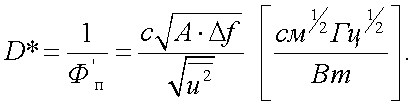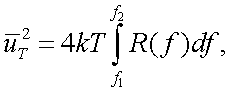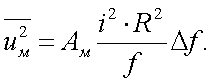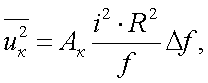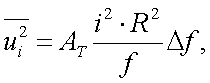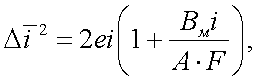В зависимости от характера физических процессов, протекающих в приемниках при преобразовании энергии излучения, они делятся на следующие основные группы: фотоэлектрические, тепловые, оптико-акустические, фотохимические и т. д.
В оптико-электронных системах наиболее широкое применение находят фотоэлектрические и тепловые приемники.
Фотоэлектрическое действие излучения может проявляться различным образом. Если под действием поглощающего потока излучения из вещества в вакуум эмитируются электроны, то имеет место внешний фотоэффект.
Внутреннее возбуждение кристаллической решетки полупроводникового материала под действием поглощающего излучения, обуславливающего перевод электронов из связанных состояний в свободное без выхода наружу, носит название внутреннего фотоэффекта. Появление свободных зарядов, способных перемещаться в твердом теле, приводит к изменению электропроводности материала чувствительного слоя; фотоэлементы, основанные на фотопроводимости, т. е. на изменении электропроводности под действием падающего оптического излучения называются фотосопротивлением. Явление внутреннего фотоэффекта возникает в системах, состоящих из двух различных контактирующих веществ (металл – полупроводник, два полупроводника) и вызывает возникновение фото-ЭДС на границах системы при облучении приконтактной области. Это явление внутреннего фотоэффекта известно как вентильный фотоэффект. Фотоэлементы, основанные на данном фотоэффекте называются вентильными фотоэлементами или фотоэлементами с запирающим слоем. Фототок в цепи вентильных фотоэлементов возникает при отсутствии внешнего питающего напряжения.
Если в качестве ионизирующих веществ применяются полупроводники с различным типом проводимости, то, наряду с возникновением разности потенциалов между слоями с p- и n-проводимостью, образуется разность потенциалов вдоль p-n-перехода. Эту фото-ЭДС называют продольной или боковой. Фотоэлементы, основанные на использовании продольной фото-ЭДС, называются фотоэлементами с продольным или боковым фотоэффектом.
Продольный фотоэффект проявляется только при неравномерном освещении чувствительного слоя. Вентильные фотоэлементы на основе электронно-дырочных переходов, работающие с приложенным внешним напряжением, называют фотодиодами.
Кроме того, приемниками могут быть и системы, похожие на фотодиоды, но обладающие внутренним усилением фототока, их называют фототриоды или фототранзисторы.
Тепловые приемники реагируют на повышение температуры чувствительного слоя. В этой группе приемников энергия квантов падающего излучения распределяется равномерно между частицами вещества фотослоя. Поэтому они, как правило, обладают неселективной чувствительностью, т.е. одинаково реагируют на излучение всех длин волн. Нагрев чувствительного слоя обнаруживается по возникновению термо-ЭДС в термоэлементах и по изменению сопротивления в болометрах и термисторах, которые входят в группу тепловых приемников.
Параметрами приемников оптического излучения обычно называют величины, характеризующие свойства приемника при работе его в определенных условиях и служащие критериями оценки его качества. При проектировании ОЭС выбор приемника в качестве его узла осуществляется по параметрам и характеристикам приемника. Рассмотрим основные параметры приемников, с которыми приходится иметь дело разработчику ОЭС, в том числе, оптику-конструктору и оптику-технологу.
Чувствительность на данной длине волны – это отношение излучения измеренной электрической величины, вызванное падением на приемник излучения, к изменению количественной характеристики этого излучения:
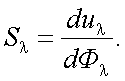
Интегральная чувствительность S – это мера реакции приемника на сложный по спектру поток излучения:
 |
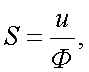(6.1) |
где u –реакция приемника на сложный поток излучения Ф.
Если воспользоваться понятием спектральной чувствительности
Sλ приемника, которая, вообще говоря, является характеристикой приемника, то вывод выражения для интегральной чувствительности S можно получить следующим образом.
Так как
 |
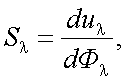(6.2) |
то
 |
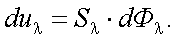(6.3) |
В свою очередь, приращение потока равно:
 |
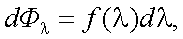(6.3') |
где fλ – спектральная плотность потока оптического излучения.
Тогда для (6.3) имеем:
 |
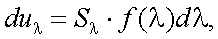(6.4) |
а для реакции u на сложное излучение:
 |
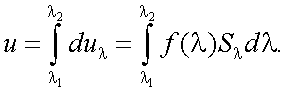(6.5) |
Если 
, то (6.5) имеет вид:
 |
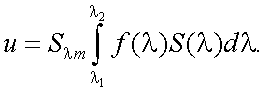(6.6) |
С другой стороны, учитывая (6.3), можно записать
 |
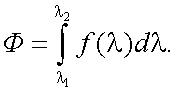(6.7) |
Тогда, подставив (6.6) и (6.7) в (6.1), имеем:
 |
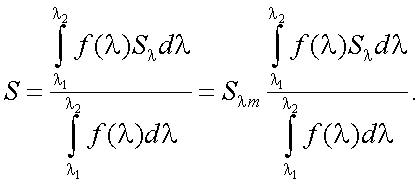(6.8) |
Из (6.8) видно, что интегральная чувствительность S зависит от характера функции спектральной плотности потока f(λ) излучателя. Следовательно, S зависит не только от свойств приемника, но и от характеристик излучения объекта. Поэтому, при исследовании чувствительности S обязательно указываются параметры излучателя, по которому определяется чувствительность. Приводимые в паспортах приемников значения S обычно измеряются по излучению эталонных источников:
- источник типа А – это АЧТ с Т = 2848 К;
- источник типа Б – АЧТ с Т = 2500 К;
- источник типа В – это АЧТ с Т = 2900 К.
В качестве эталонного источника при измерении паспортной чувствительности сопротивлений для ИК области используется еще АЧТ при Т = 373 К или Т = 573 К.
В США параметры фотосопротивлений чаще всего измеряются по излучению АЧТ с Т = 500 К.
В последнее время так делается и в России. Это позволяет сравнивать чувствительности отечественных и зарубежных приемников излучения.
Коэффициент использования приемников излучения представляет собой отношение интегралов в соответствии с формулой (6.8), рис. 6.1.
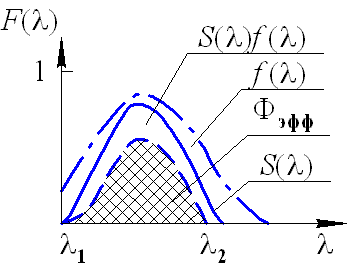
Рис. 6.1. К выводу выражения для коэффициента использования приемников
 |
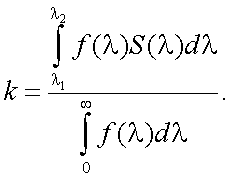(6.9) |
Этот коэффициент показывает, какую долю сложного потока излучения, падающего на приемник, составляет эффективный для этого приемника поток; тогда (6.9) можно записать в виде:
 |
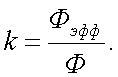(6.9') |
Коэффициент использования, как правило, определяется графическим или численным интегрированием.
Рассмотрим расчет этого коэффициента для излучения АЧТ. Если в качестве источника излучения берется АЧТ, то спектральная плотность потока излучения АЧТ f(λ) имеет вид:
 |
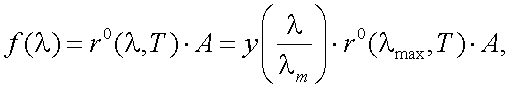(6.10) |
где А – площадь фоточувствительного слоя;
 |
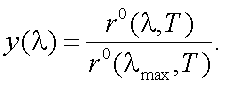(6.11) |
Тогда
 |
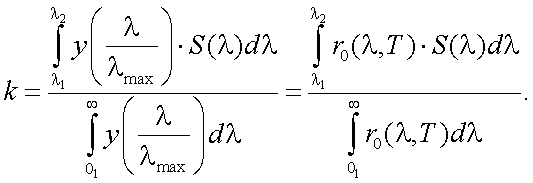(6.12) |
Если эффективный поток нормировать не на поток в интервале λ1 – λ2, а на поток в бесконечно большом интервале, знаменатель в формуле (6.12) равняется:
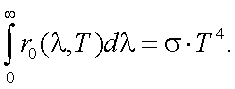
Теперь в (6.11) светимость r0(λ, T) примет следующий вид:
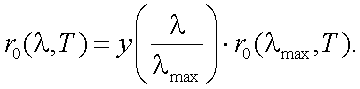
Тогда коэффициент использования излучения будет следующим:
 |
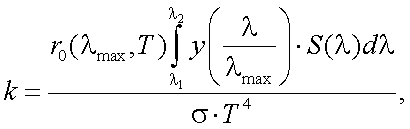(6.13) |
где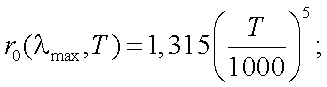 
σ – постоянная Стефана – Больцмана;
– на основании закона Голицына – Вина.
Подставляя в (6.13) числовые значения r0(λmax, T) и σ, получим:
 |
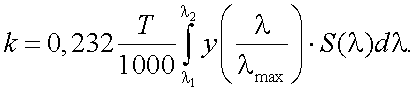(6.14) |
Заменяя интеграл в (6.14) суммой, можно получить:
 |
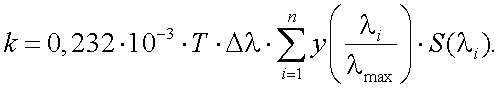(6.15) |
Значение функции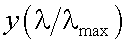 
приведена в учебниках (см., например, Ю.Г. Якушенков. Физические основы оптико-электронных приборов. – М.: Сов. радио, 1965. – С. 33).
Коэффициент использования и интегральная чувствительность S могут определить Sλ, т.е. спектральную чувствительность в абсолютных единицах.
Действительно, согласно (6.8) и (6.9) имеем:
 |
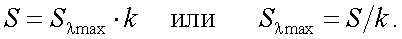(6.15') |
Спектральная чувствительность Sλ может быть представлена как:
 |
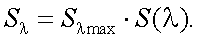(6.16) |
Учитывая по формуле (6.15) значение Sλmax, формула (6.16) тогда примет вид:
 |
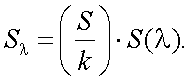(6.17) |
Пороговым потоком Фп называется минимальный поток излучения, который вызывает на выходе приемника сигнал, эквивалентный уровню собственных шумов.
Если 
, то заменяя Ип через среднеквадратичное значение шумов, применительно к Фп получаем:
 |
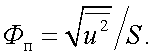(6.18) |
Иногда принимают, что пороговый поток Фп имеет вид:
 |
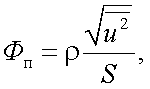(6.19) |
где ρ – коэффициент пропорциональности > 1.
Ниже мы будем рассматривать структуру шумов приемника, пока же следует указать, что среднеквадратичное значение шумов зависит от размеров площадки А и полосы пропускания Δf электрической схемы включения приемника; таким образом пороговый поток есть функция А и Δf.
 |
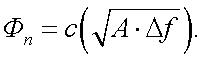(6.20) |
Поэтому для более объективного сравнения различных типов ПЛЭ принято выражать пороговый поток для единичной полосы частот и единичной площади чувствительного слоя:
 |
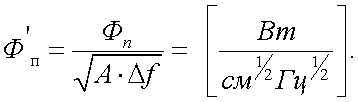(6.21) |
Этот пороговый поток называется приведенным к единичной полосе частот и единичной площади чувствительного слоя.
Иногда в расчетах удобно пользоваться величиной, обратной Ф′п, впервые введенной Р.К. Джонсом и названной способностью к обнаружению:
 |
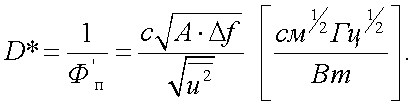(6.21') |
В настоящее время её используют как в России, так и за рубежом.
Шумами приемника оптического излучения называют сигналы с переменной амплитудой и частотой, возникающие на его выходе при включении в схему.
1. Тепловой шум (шум Джонсона).
Свободные электроны в любом проводнике, в том числе и в приемнике лучистой энергии, находятся в состоянии хаотического теплового движения. В результате этого в любой момент времени число электронов, движущихся вдоль проводника в одном направлении, не равно числу электронов, движущихся в противоположном направлении. Поэтому на зажимах проводника возникает флуктуационная ЭДС, дисперсия которой в интервале частот Δf = f1 - f2 определяется формулой Найквиста:
 |
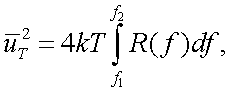(6.22) |
где Т – абсолютная температура чувствительности слоя;
k – постоянная Больцмана, численно равная 1,38·10-23 Дж/град.
R(f) – функция, описывающая зависимость сопротивления от f.
2. Дробовой шум.
Электрический ток, является потоком электронов, т.е. потоком дискретных частиц. Величина тока определяется числом этих частиц, которое флуктуирует во времени, что приводит к появлению дробового шума. Величина этой флуктуации определяется из статистических соображений [1] и выражается формулой Шоттки.
 |
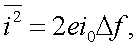(6.23) |
и
 |
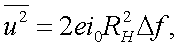(6.24) |
где е – заряд электрона;
i0 – среднее значение тока;
Δf – полоса частот;
RН – сопротивление нагрузки.
3. Токовый шум (1/f – шум).
Природа этого шума до сих пор недостаточно исследована. Предполагают, что составляющими его являются: генерационно-рекомбинационный, модуляционный и контактный шумы, так что это название в значительной степени условно.
Генерационно-рекомбинационный шум возникает из-за флуктуаций числа и времени жизни токоносителей, образованных при термовозбуждении. Простого и общего выражения для этого вида шумов не существует.
Модуляционный шум иногда называют также избыточным, что обычно выражается как:
 |
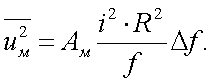(6.25) |
Контактный шум обусловлен плохим качеством контактов, имеет следующее выражение:
 |
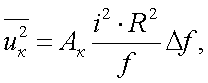(6.26) |
где Ам и Ак – некоторые постоянные.
Поэтому, в общем виде выражение для токового шума можно записать:
 |
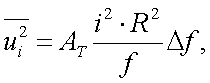(6.27) |
где АТ – постоянная, которая зависит от типа приемника; например, для PbS АТ = 10-11…10-12.
4. Радиационный шум.
Наряду с шумами, присущими самому приемнику, флуктуации сигналов на выходе ПЛЭ могут возникнуть из-за флуктуации излучения фона, падающего на приемник с площадью
А, имеющего коэффициент излучения εТ. Выяснено, что флуктуации мощности излучения вызывают радиационный шум, определяемый по следующей формуле:
 |
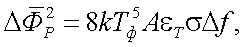(6.28) |
где k – постоянная Больцмана;
σ – постоянная Стефана – Больцмана;
Тф – температура фона.
5. Тепловые флуктуации.
Температура приемника определяется статистическим обменом энергии между телом приемника и окружающей средой. Эта температура будет всегда колебаться около некоторой средней величены Тп. Отсюда и появляется тепловой шум, который возникает, из-за того, что приемник сам является излучателем с температурой Тп.
В работе [1] отмечено, что мощность излучения, вызывающая тепловые флуктуации приемников, имеет вид:
 |
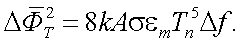(6.29) |
6. Шум мерцания (фликкер-эффект).
Шум мерцания обусловлен случайными изменениями эмиссии фотокатода.
Установлено, что шум мерцания зависит от типа материала и свойств чувствительного слоя. Выражение для шума мерцания имеет вид:
 |
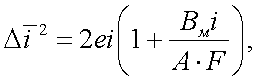(6.30) |
где Bм – постоянная величина, характеризующая природу фотокатода.
