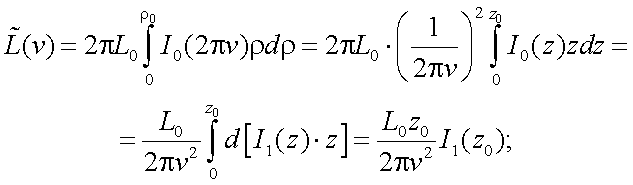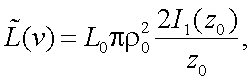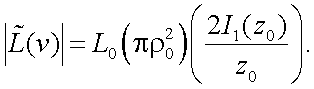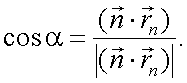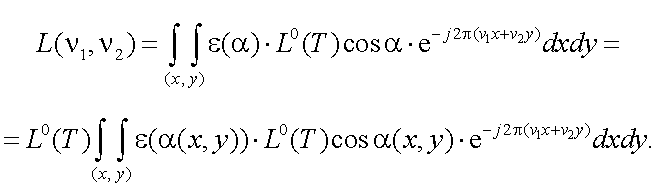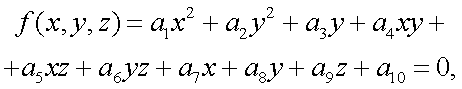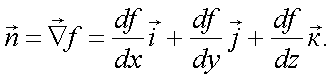5.1. Оптическая система (ОС)
Одним из наиболее важных узлов ОЭП и С является оптическая система. Структура оптической системы ОЭП и С может быть различной в зависимости от способа работы всего прибора и от стоящих перед ним задач.
Обобщенные структурные схемы оптических систем активных (а) и пассивных (б) ОЭП приведены на рис. 5.1.
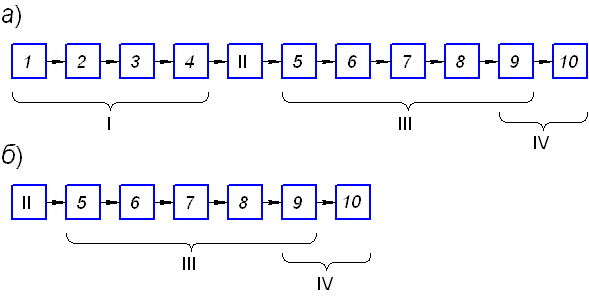
Рис. 5.1. Структурные схемы оптических систем активных (а) и пассивных (б) ОЭП:
I – передающая система; II – объект исследования; III – приемная система; IV – электрическая система;
1 – источник излучения, 2 – модулятор, 3 – фильтр, 4 – оптическая система осветителя, 5 – объектив, 6 – компенсатор, 7 – оптический анализатор, 8 – конденсор, 9 – приемник излучения, 10 – усилитель сигнала
Основными задачами, решаемыми оптическими системами ОЭП, являются:
1) обзор части пространства, в которой находится объект поиска, ориентир или объект наблюдения;
2) анализ оптического изображения объекта в определенном масштабе с целью последующей его регистрации;
3) обеспечение требуемой освещенности на поверхности приемника излучения;
4) концентрация потока излучения искусственных источников;
5) определение угловых координат объектов и дальности до них.
Оценку свойств, качества и эффективности действия оптических систем (ОС) приборов проводят с помощью ряда характеристик, которые можно разделить на следующие группы:
– технико-экономические и эксплуатационные;
– габаритные;
– энергетические;
– аберрационные;
– пространственно-частотные.
Габаритные характеристики ОС.
Основными характеристиками этой группы являются: фокусное расстояние f’, поле зрения 2ω, относительное отверстие qо, или диаметр входного зрачка Dвх. зр., и разрешающая способность V.
Исходя из рис. 5.2, линейное увеличение определяется по формуле:
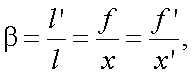 |
(5.1) |
а угловое увеличение равно
 |
(5.2) |
где
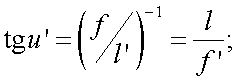
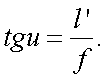
Подставив последние два выражения в формулу (5.2), получим
 |
(5.3) |
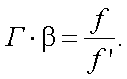 |
(5.3') |
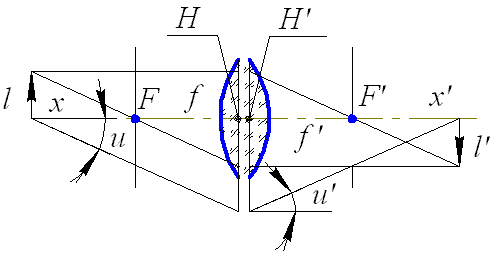
Рис. 5.2. Схема построения изображения в эквивалентной схеме ОС
Оптическая сила определяется по формуле:
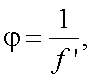 |
(5.4) |
а телесный угол поля зрения 2ω выражается через фокусное расстояние и диаметр полевой диафрагмы
Dп следующим образом:
 |
(5.5) |
Следует отметить, что относительное отверстие 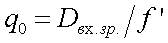 определяет освещенность в изображении объекта, т.е. оказывает влияние на энергетические характеристики ОС.
определяет освещенность в изображении объекта, т.е. оказывает влияние на энергетические характеристики ОС.
5.2. Энергетические характеристики ОС
Рассмотрим методику расчета энергетических характеристик ОС, основными из которых являются: освещенность в изображении объекта Eиз, светосила
H, коэффициент пропускания τ0 и матрица пропускания τij. Для этого определим поток оптического излучения от объекта на входе ОС:
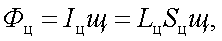 |
(5.6) |
где Lц – энергетическая яркость цели с площадью S в направлении ОЭП, подробно методы расчета которой нами рассматривались выше.
Величина потока Физ, создающего изображение объекта, будет
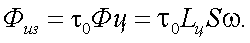 |
(5.7) |
Из геометрических соображений, и согласно рис. 5.3, имеем:
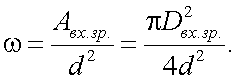 |
(5.8) |
Тогда, используя (5.7) и (5.8), имеем:
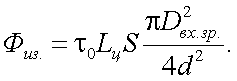 |
(5.9) |
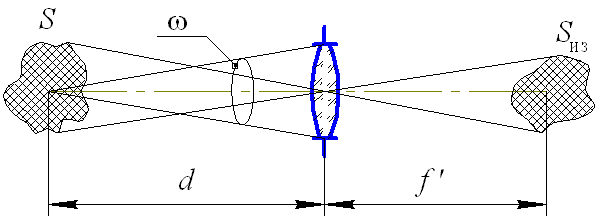
Рис. 5.3. К методике расчета энергетических характеристик ОС
Согласно рис. 5.3,
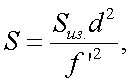
то для освещенности изображения Eиз имеем:
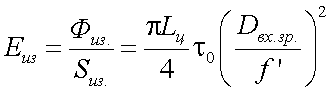 |
(5.10) |
или
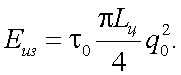 |
(5.11) |
В поляризованном свете (рис. 5.4) освещенность в изображении объекта Еiиз определяется по формуле:
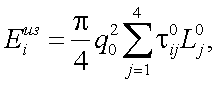 |
(5.12) |
где τ0ij – матрица пропускания оптической системы;
Lj0 – вектор-параметр Стокса излучения на входном зрачке оптической системы.
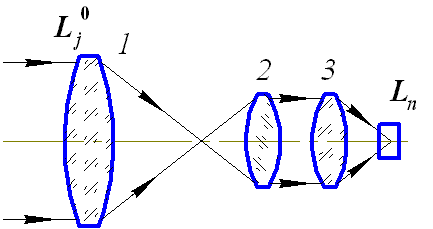
Рис. 5.4. К методике расчета освещенности в изображении объекта в поляризованном свете
Следует заметить, что коэффициент пропускания оптической системы τ-0 определяется по формуле:
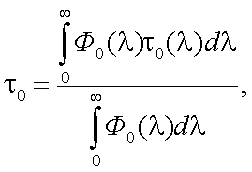 |
(5.13) |
где Ф0(λ) – спектральная плотность потока оптического излучения на входном зрачке ОС.
Рассмотрим методику определения матрицы пропускания ОС, состоящей, например, из трех линз.
Допустим, что вектор-параметр Стокса для яркости входящего в ОС излучения есть Lj0, а матрицы пропускания оптических элементов 1, 2, 3 обозначим через τij(1), τik(2) и τkn(3).
Тогда процесс прохождения поляризованного излучения через элементы 1-3 можно записать в виде:
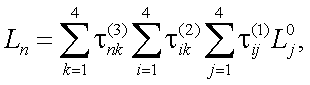 |
(5.14) |
где Ln – компоненты вектора параметра Стокса яркости излучения на выходе ОС.
Выражение (5.14) показывает, что операция умножения проходит справа налево в той последовательности, которая соответствует ходу лучей в ОС.
В тех случаях, когда необходимо определить коэффициент τ0(λ) большого числа преломляющих и отражающих элементов, то он определяется по формуле:
 |
(5.15) |
где ρnλ – спектральный коэффициент отражения преломляющих поверхностей;
m – число преломляющих поверхностей;
ρзλ – спектральный коэффициент отражения зеркальных отражающих поверхностей,
n – число зеркально отражающих поверхностей;
τl(λ) – спектральный коэффициент пропускания, учитывающий только поглощение внутри оптического материала толщиной l по закону Бугера – Ламберта – Бера.
5.3. Пространственно-частотные характеристики (ПЧХ) ОС
ПЧХ характеризует реакцию ОС на входное воздействие.
Рассмотрим случай, когда в поле зрения прибора имеется светящийся объект, распределение яркости по поверхности которого описывается функцией L(x, y). Освещенность изображения точки, имеющей координаты (x, y), в идеальной оптической системе, т.е. системе без аберраций и дифракционного рассеяния, равна определенному значению. Тогда в других точках плоскости изображения она равна нулю.
В реальной оптической системе дифракционное рассеяние и аберрации вызывают размытие светящейся точки по пятну рассеяния, в результате чего освещенность в некоторой точки (x′, y′) плоскости изображения оказывается отличной от нуля. Степень размытия изображения характеризуется функцией рассеивания H(x′, y′), которая представляет собой закон изменения освещенности в точке (x′, y′), когда из точки (x, y) направляем поток, равный единице.
Так как весь размытый поток должен быть равен исходному падающему потоку, то
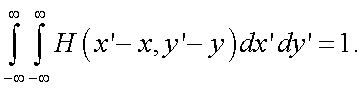 |
(5.16) |
Рассмотрим распределение освещенности в изображении, когда имеется совокупность светящихся точек, составляющих объект наблюдения.
В этом случае из элементарной площадки dx•dy вокруг точки (x, y) падает поток излучения kL(x, y)dxdy; в точке же (x′, y′) этот поток создает освещенность
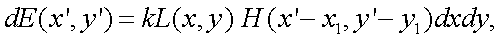 |
(5.17) |
где к = πτ0Sin2γ.
Полная освещенность в точке (x′, y′) равна сумме возникающих из-за рассеяния потоков, исходящих из всех элементов dx•dy.
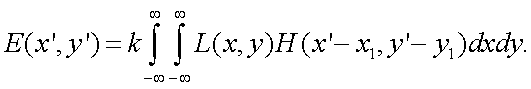 |
(5.18) |
Получаемый интеграл является интегралом свертки двух функций и показывает распределение освещенности E(x', y') изображения при заданном изменении яркости L(x, y) объекта в совокупности с функцией рассеяния каждой точки изображения.
Преобразование Фурье функции E(x', y') позволяет получить пространственно-частотный спектр
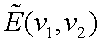 распределения освещенности изображения:
распределения освещенности изображения:
 |
(5.19) |
где 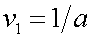 ;
; 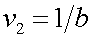 ; где a и b – периоды первых гармоник по соответствующим осям X и Y.
; где a и b – периоды первых гармоник по соответствующим осям X и Y.
Заменив переменные X = x' - x и Y = y' - y и преобразовав (5.19), получим:
 |
(5.20) |
Выражение (5.20) показывает, что энергетический пространственно-частотный спектр распределения освещенности в плоскости изображения равен преобразованию Фурье функции распределения яркости объекта (функции рассеяния) оптической системы.
Сокращенно (5.20) можно представить в виде
 |
(5.21) |
причем 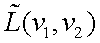 называется ПЧС распределения яркости объекта, а
называется ПЧС распределения яркости объекта, а 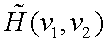 – комплексной пространственно-частотной передаточной функцией оптической системы.
– комплексной пространственно-частотной передаточной функцией оптической системы.
Из (5.21) следует, что оптическая передаточная функция ОС может быть получена, как отношение частотных спектров освещенности изображения и яркости объекта:
 |
(5.22) |
Функция 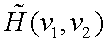 является комплексной. Ее модуль |
является комплексной. Ее модуль |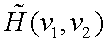 | называется модуляционной передаточной функцией оптической системы.
| называется модуляционной передаточной функцией оптической системы.
Иногда в литературе эту величину называют амплитудно-пространственно-частотной характеристикой (АПЧХ) или контрастно-частотной характеристикой (КЧХ).
5.4. Пространственно-частотные характеристики (ПЧХ) объектов наблюдения
1. ПЧХ точечного источника.
Математической моделью точечного источника излучения является двумерная дельта-функция, т.е.
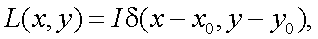 |
(5.23) |
где I – сила света источника в данном направлении.
Спектр точечного источника определяем по следующей формуле:
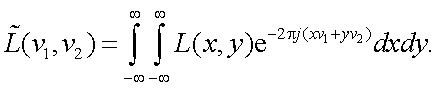 |
(5.24) |
Если (5.23) подставить в (5.24), то имеем с учетом фильтрующего свойства дельта-функции:
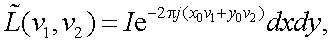
здесь 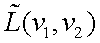 – пространственно-частотный спектр яркости объекта, а амплитудно-частотная характеристика (АЧХ) представляется модулем
– пространственно-частотный спектр яркости объекта, а амплитудно-частотная характеристика (АЧХ) представляется модулем 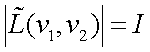 , т. е. является const на всех частотах, а фазово-частотная характеристика (ФЧХ) равна: ψ(ν1, ν2)=2π(ν1x0 + ν2y0).
, т. е. является const на всех частотах, а фазово-частотная характеристика (ФЧХ) равна: ψ(ν1, ν2)=2π(ν1x0 + ν2y0).
2. ПЧХ объекта прямоугольной формы, рис. 5.5.
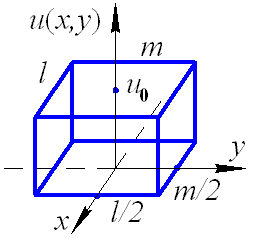
Рис. 5.5. К определению пространственно-частотного спектра объекта прямоугольной формы
Допустим, что Lxy = L0 = const.
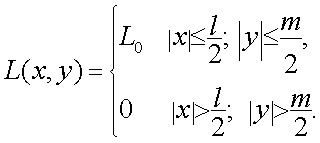 |
(5.25) |
Пространственно-частотный спектр равен:
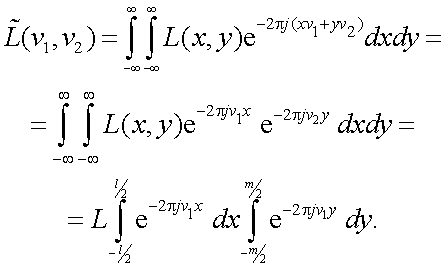 |
(5.26) |
Интегралы в (5.26) равны:
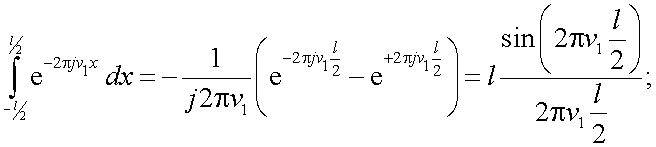

Тогда имеем:
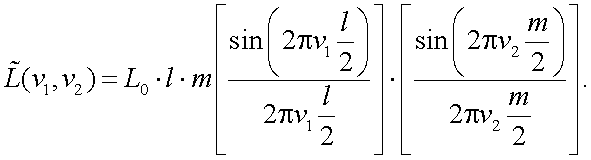 |
(5.27) |
С учетом функции Sin с модуль ПЧС запишется в виде:
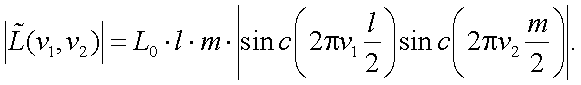 |
(5.28) |
Для получения нормированного вида модуля ПЧС объекта, выражение (5.28) необходимо разделить на L0 (рис. 5.6)
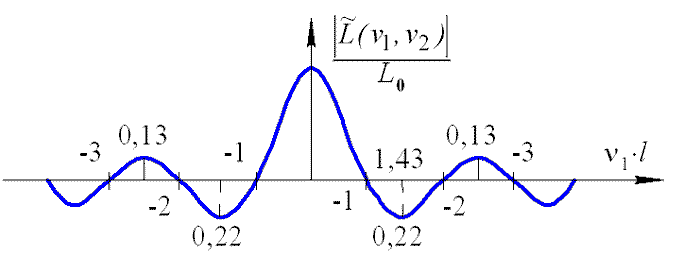
Рис. 5.6. Нормированный вид модуля ПЧС объекта прямоугольной формы по координате ν1
3. ПЧХ круглого объекта равномерной яркости.
Согласно рис. 5.7, яркость объекта зависит от цилиндрических координат ρ и φ следующим образом:
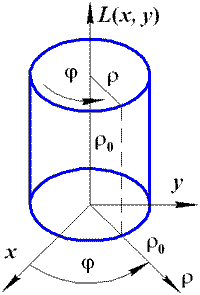
Рис. 5.7. Геометрия объекта с равномерной яркостью L0
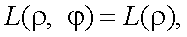 |
(5.29) |
где
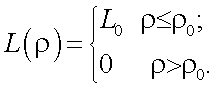
На основании прямого преобразования Фурье имеем:
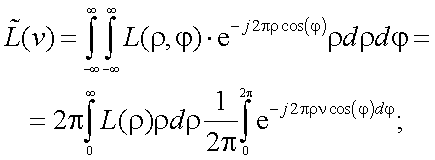 |
(5.30) |
обозначим интеграл
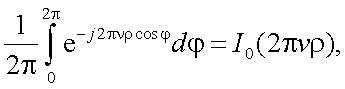
где I0 – функция Бесселя нулевого порядка.
Тогда для соотношения (5.30) получим:
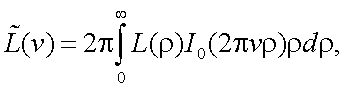 |
(5.31) |
или с учетом (5.29)
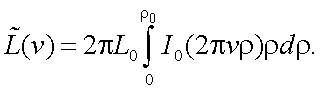 |
(5.32) |
Для вычисления интеграла в (5.32) воспользуемся формулой приведения бесселевых функций:
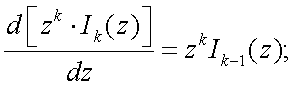
в нашем случае k = 1, поэтому
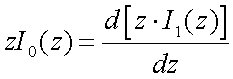 . . |
(5.33) |
Введем обозначение: z = 2πνρ.
Тогда
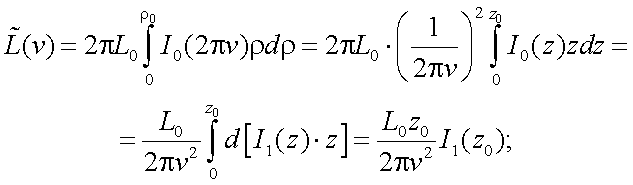
так как z0 = 2πνρ0;, то имеем:
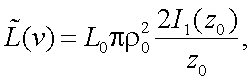
откуда получаем, что ПЧХ данного объекта равна
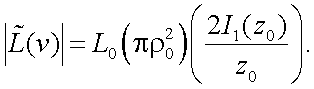 |
(5.34) |
5.5. Спектры собственного излучения сложных тел и использование их для распознавания формы
Рассмотрим объект сложной формы, излучающий по законам теплового излучения (рис. 5.8).
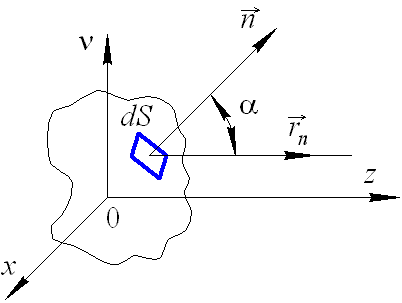
Рис. 5.8. К вопросу о свойствах собственного излучения сложных тел
Тогда распределение яркости теплового излучения по поверхности объекта представится в виде:
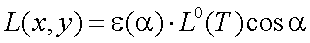 ,
,
где, согласно рис. 5.8, α – угол между нормалью  к элементу dS поверхности объекта и направлением на наблюдателя, которое характеризуется вектором
к элементу dS поверхности объекта и направлением на наблюдателя, которое характеризуется вектором 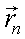 ;
;
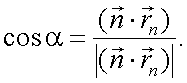
С использованием прямого преобразования Фурье, пространственно-частотный спектр получается в виде:
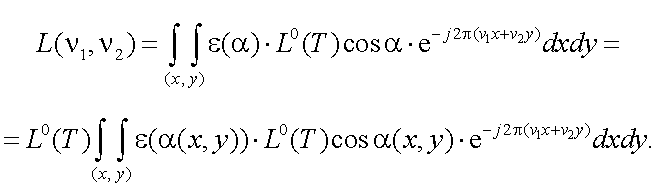 |
(5.35) |
Если поверхность объекта описывается уравнением:
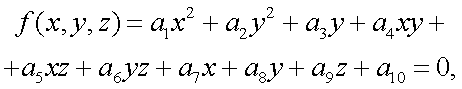 |
(5.36) |
где аi (i = 1, 2, 3…9, 10) – коэффициенты, характеризующие форму объекта,
то, согласно работе [29], локальную нормаль 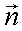 определим по формуле:
определим по формуле:
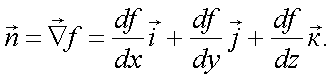 |
(5.37) |
В свою очередь, вектор наблюдателя 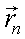 в сферической системе координат представляется в виде:
в сферической системе координат представляется в виде:
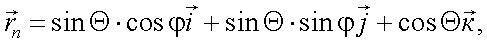 |
(5.38) |
где 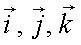 – единичные орты координатных осей ох, oy, oz.
– единичные орты координатных осей ох, oy, oz.


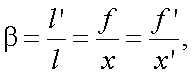

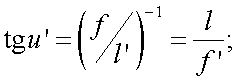
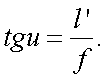

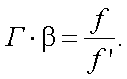

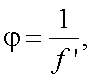
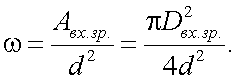
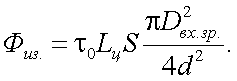

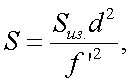
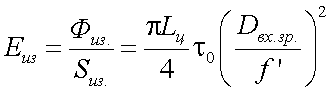
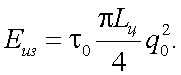
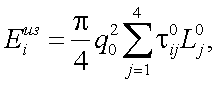

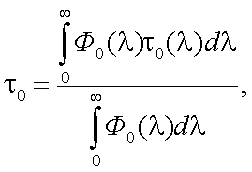
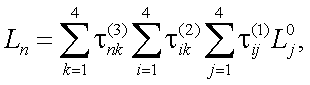
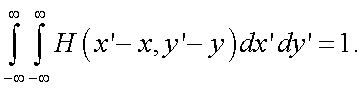
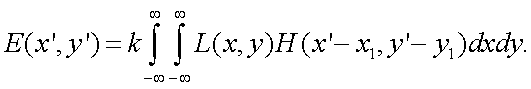



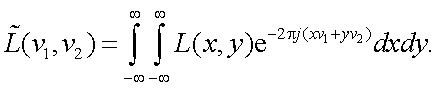
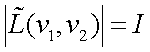 , т. е. является const на всех частотах, а фазово-частотная характеристика (ФЧХ) равна: ψ(ν1, ν2)=2π(ν1x0 + ν2y0).
, т. е. является const на всех частотах, а фазово-частотная характеристика (ФЧХ) равна: ψ(ν1, ν2)=2π(ν1x0 + ν2y0).
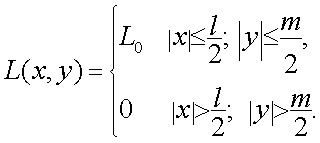
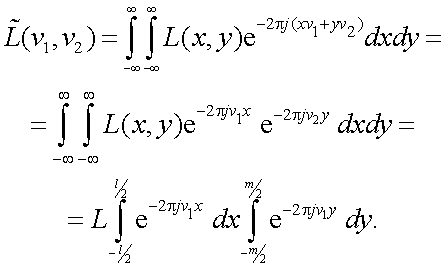
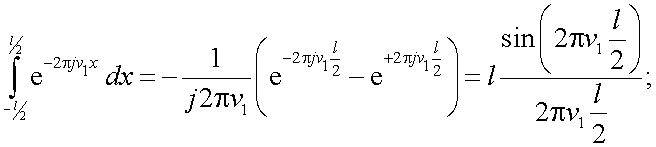

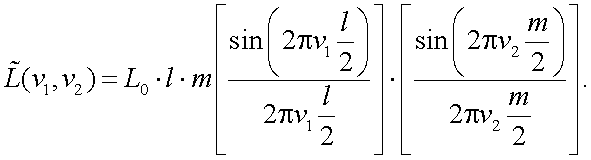
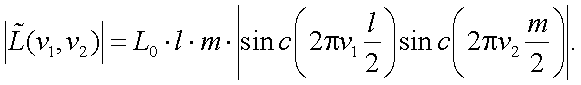


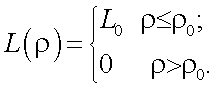
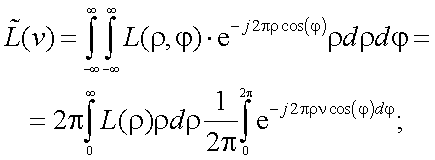
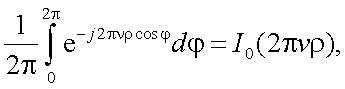
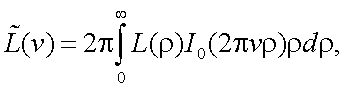
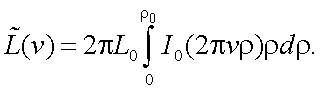
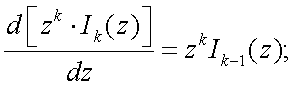
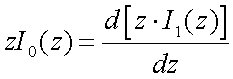 .
.